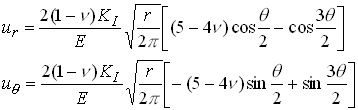EN224:
Linear Elasticity
EN224:
Linear Elasticity 
Division of Engineering
6.5 Example Problems Using Airy Stress Functions
There are many excellent textbooks which describe in great detail the use of Airy functions to solve plane problems in elastostatics. We will not repeat this material here. Instead, we will illustrate the general idea by solving a particular problem, which has some practical significance.
Asymptotic Crack Tip Field: The Williams Solution.

Consider an infinite solid, which contains a semi-infinite crack on the (x1,x3) plane. Suppose that the solid deforms in plane strain and is subjected to bounded stress at infinity. Find the state of stress near the crack tip.
We will attempt to find an Airy stress function satisfying
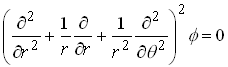
with
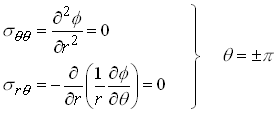
and with vanishing stress at infinity.
Try a solution of the form
Substituting into the governing equation for the Airy function, we find that
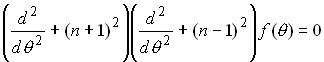
which is satisfied by
The stress components therefore follow as

To ensure that the crack faces are free of tractions, we must set
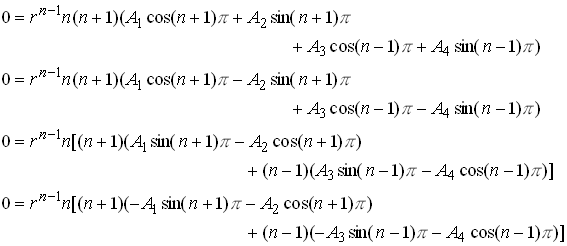
Evidently n=0 is a (not very interesting) solution. To find others, simplify by adding and subtracting pairs of equations to see that
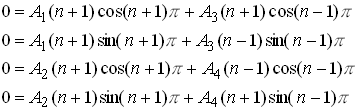
Both the first pair of equations and the second pair have nonzero solution if
whence
Solutions with ![]() evidently generate stresses which do not decay at infinity
and so must be rejected.
evidently generate stresses which do not decay at infinity
and so must be rejected.
Solutions with ![]() have
have
(or more singular) and consequently have unbounded strain energy. These solutions are normally rejected on these grounds. However, we happily live with unbounded strain energies when solving problems involving dislocations, so this explanation is not entirely satisfactory. Retaining only the solutions with bounded strain energy does guarantee uniqueness, however, and a successful theory of linear elastic fracture mechanics has been based on this assumption.
Substituting for n in the four equations above shows that
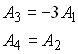
The remaining coefficients are arbitrary, and are determined by the nature of the loading at infinity.
It is common to set
Where![]() are mode I and mode II stress intensity factors for
the crack. The mode I stress intensity factor characterizes the symmetric
terms (and corresponds to loading applied so as to open the crack) while
the mode II stress intensity factor characterizes the anti-symmetric terms
and corresponds to loading applied so as to shear the crack. These parameters
are defined so that
are mode I and mode II stress intensity factors for
the crack. The mode I stress intensity factor characterizes the symmetric
terms (and corresponds to loading applied so as to open the crack) while
the mode II stress intensity factor characterizes the anti-symmetric terms
and corresponds to loading applied so as to shear the crack. These parameters
are defined so that
The factor![]() is introduced so that the expression for energy release
rates at the crack tip in terms of the stress intensity factors has a simple
form.
is introduced so that the expression for energy release
rates at the crack tip in terms of the stress intensity factors has a simple
form.
In terms of stress intensity factors, the asymptotic crack tip field is:

The displacement field may be computed by integrating the strains, with the result