EN224: Linear Elasticity   

  Division of Engineering

 

8.5 The Principle of Stationary and Minimum Complementary Energy

In our potential energy formulation, we considered a family of kinematically admissible displacement fields, and defined V(v) so that the elastostatic state minimized V.

We can devise an alternative variational method in which we consider a family of statically admissible stress fields, and define complementary energy so that the elastostatic stress field minimizes C.

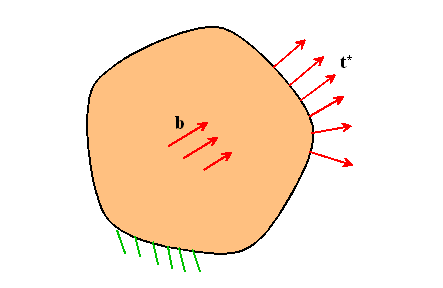
Let us make this precise.

Let with

In addition, define the components of the compliance tensor such that

Now, define a statically admissible stress field which satisfies

Define the strain energy density associated with as

Define the complementary energy C as

We will proceed to show several important properties of C.

(1) C is stationary for

(2) If C is stationary for some , then

(3)

 

The Principle Of Stationary Complementary Energy

C is stationary if and only if with on .

Proof. We will show first that if with on then C is stationary.

 

Begin by computing the first variation of C. We could use the same procedure we followed in discussing the principle of stationary potential energy, but just for variety, we will this time use the formal machinery of the calculus of variations.

 

First, let us define a statically admissible variation in stress Let

where

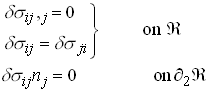
Then, the first variation of C is defined as

Hence

Note that we may write

where we have used the symmetry of .

Now, substitute into the expression for and integrate by parts

where we have noted that on , while on .

This completes the first part of the proof.

 

 

Next, consider the converse. We wish to show that if C is stationary, then , with on .

 

If C is stationary, then

In particular, choose

where is a tensor function of position and is the permutation symbol. One may readily verify that

as required for a statically admissible variation. Hence

Now, recall that , so we may choose and on . Then, integrate by parts twice to see that

Since this holds for all , it follows that

This is the strain equation of compatibility (See Section 1.5) and implies (at least for a simply connected region) that there exists a single valued displacement with

Finally, we need to show that . Follow the procedure in the first part of the proof to see that

Then, choose

to obtain the required result.

 

 

The Principle of Minimum Complementary Energy

 We will now go a step further, and show that C is a global minimum only for the compatible stress field. We could show this using the procedure we used to prove minimum potential energy, but just for variety we will do things slightly differently.

 

As before, let with

In addition, define the components of the compliance tensor such that

 

Define a statically admissible stress field which satisfies

 

Denote the strain energy density associated with as

and define

 

Now, consider

Noting that both and are equilibrium fields, we may write

Integrate by parts

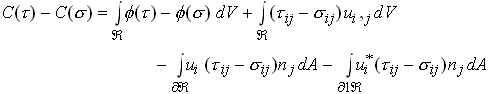
The last two integrals evidently sum to zero if and . Expand the remaining terms in terms of strains

Finally, using the properties of the stiffness tensor, we see that

with equality if and only if .