
In the case we're describing, the charges are stationary, not allowed to move: Electrostatics.
Review of Core Material Relevant to EN123
(1)
Resistors & Ohm's Law
We
would like to start
with Ohm's Law, Voltage = Current X Resistance, V = I * R.
But first let's get comfortable with voltage, current and resistance.
For voltage we start
with Coulomb's Law, from E&M class: "opposites attract, likes repel."

In the case we're describing, the charges are stationary, not allowed to move:
Electrostatics.
Voltage between
points P and G is any path integral from G to P over the conservative E field.
![]()
Ground
vs common vs reference
Define current as
charge flow, Q/sec. But given a "pressure" in the form of voltage,
and a pathway of resistance R, Ohm's Law says
I=Q/t,
and implies charges moving at a constant terminal velocity. (Corn syrup demo).
Contrast with acceleration of charge is a vacuum or plasma... F=m*a? not for Ohm's Law...
The charge on an
electron is negative, so a positive current arrow implies electron flow in the
oppositie direction.
Ohm's
Law is about resistance.
Calculating resistance
R = rho*Length/Area, where rho is resistivity, a material property. What is
effect of increasing temperature on resistance? For metals, increasing resistance,
for semiconductors, decreasing.
* Measuring resistance; tolerance; resistor color code
Voltage divider:
 Vout = (R2/(R2+R1)) * Vcc
Vout = (R2/(R2+R1)) * Vcc
Potentiometer (show and tell aircraft angle sensor; servo motor component... )
Resistors
in series, parallel. G = 1/R ; conductance.

and what about 3 R's in parallel? add conductances.

Current
flow through by ions through membrane channels
ions as charge carriers in aqueous solution. electrochemistry.
Power = Voltage * Current = V^2/R = I^2*R
Resistors dissipate energy, heat up. Demo: 1/4 watt resistor trying to dissipate 1W of power...
Power transfer by impedance matching...
Wheatstone bridge
Thevenin - Norton equivalents
Resistivity
rho (a material property):

Current-voltage
characteristic of a diode:
temperature dependence?!
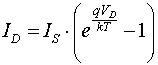
where
k is Boltzmann's constant, q is the charge on the electron and T is temperature
in Kelvin.
Note the implication, corrected below, that resistance increases with temperature...
the
Reverse saturation current Is (leakage current in the "wrong direction"):
![]()
which
implies that for every 5 degree increase in temperature the current doubles.
demo: ON voltages of p-n junction diode, green LED, Schottky diode
0.6, 1.7. 0.2v
Zener diodes as voltage references (H&H p. 44ff).
full wave rectifier: Wheatstone bridge again...
* Resistance through pipe:

http://www.emedicine.com/radio/byname/basic-fluid-dynamics-principles---application-to-percutaneous-intervention.htm
node
admittance matrix: KCL: current flow into a node is negative.
V = inv(nY)*Is
which can
with a little practice be written down by inspection...
example with all-resistor network: node voltages, branch currents.
---------------- ------------------- --------------------- end of Resistors
(2)
The Leaky Integrator, and capacitance C.
Next,
a hydraulic analogy, the leaky bucket, where voltage is like water pressure,
current is like water flow and electrical resistance is like resistance to water
flow through a pipe. See below, bucket with area A, flow in F
cc/sec, water height h, and leak coefficient G cm^2/sec
(dwg
by Jo Schulak)

Capacitance
C is analogous to area A of the bucket.
Remembering
your exposure to differential equations, and assuming an initial condition of
no water in the bucket, solve the leaky integrator equation above to find

C = Q/V; Q = C*V ; I = C dV/dt
![]() where
epsilon is the permittivity of the dielectric medium between the capacitor plates.
where
epsilon is the permittivity of the dielectric medium between the capacitor plates.
; look forward to defibrillator design...
Capacitors as sensors.
formulas for capacitors in parallel (add), in series 1/C = 1/C1 + 1/C2.
First order natural HP and LP filters, with capacitors.
Capacitors are short circuits at high frequency and open circuits at low freq...impedance...
Laplace transform; s =j*w, frequency
How impedance is different from resistance: "complex resistance"
Laplace transforms--
As you may recall from a diff eq course (AM33), the Laplace transform takes
you from the time to the "frequency" domain
and allows you to solve a differential equation "algebraically".
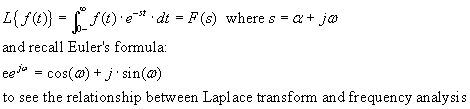
A property of the Laplace transform, given you know F(s), the Laplace transform of f(t):
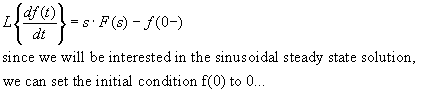
The Laplace integration property: ![]() ; see
; see
http://www.swarthmore.edu/NatSci/echeeve1/Ref/LPSA/LaplaceZTable/LaplacePropTable.html
Taking the Laplace transform of the relationship between current and voltage for a capacitor,
![]()
The low pass VCVS second order filter: output = K*V+; (See Horowitz and Hill,
chpt 5 handout, p. 273...)
define KCL: Algebraic sum of branch currents into a node equals zero.
repeat node-admittance-matrix convention: current flowing out of a node is positive...
Filter with two capacitors: Two nodes to write KCL for, end up with

solving with a dependent source.
Fourier Series, spectrum
good for a periodic function...
meaning of fundamental frequency in radians, omeg0 = 2*pi/T where T is "period"
how many unknowns are there? 20, no counting a0, the mean of the periodic
formula
calculus book formula for solving...
![]() solving another integral...
solving another integral...
but if we are recording/sampling waveform h(t) we don't know it analytically.
what about 20 equations in 20 unknowns? samples spaced how far apart?
another matrix inversion problem...
LP and HP natural first order filters.
---------------- ------------------- --------------------- end of Capacitors
(3) Inductors and Faraday's Law
Faraday's
Law

V = I * R
Q = C * V
φ = L * I
flux = phi = L * I ==> V = L dI/dt ==> V(s) = s*L*I(s)
The unit of inductance is the Henry. self inductance L, and mutual inductance M (between 2 coils).
Griffiths p. 295: calculate inductance of a solenoid radius R, length l, turns N/l: L = mu * pi * R^2*l*N...
what about minus sign in Faraday's Law? from Griffiths:
"Inductance (like capacitance) is an intrinsically positive quantity. Lenz's
Law, which is enforced by the minus sign, dictates that the EMF (voltage) is
in such a direction as to oppose any change in current. For this reason, it
is called a back EMF. Whenever you try to alter the current in a wire
you must fight againt this back EMF. Thus inductance plays somewhat the same
role in electric circuits that mass plays in mechanical systems: The greater
L is, the harder it is to change the current, just as the larger the mass, the
harder it is to change an object's velocity."
Inductors in series, in parallel.
The
circular magnetic field around a current-carrying wire:
Biot-Savart Law; Ampere's Law
How
a transformer works: primary, secondary windings
Vout =(num_sec_wind/num_pri_wind)*Vin...
demo solenoid: moving a iron piston with electrically-induced magnetic field
B
Power
supply = transformer + rectifier + LP filter + regulator
Demo
of E3631A limiting current and voltage with 4.7 ohm resistor
on 25v supply. resistance of jumpers! 2 ohms...
How a switching power supply works to have no loss at the regulator.
The role of an inductor in a defibrillator. Second order system, overdamped please.
How transformers work: http://www.scienceaid.co.uk/physics/electricity/electromagnetism.html
Lorentz
force Law
![]()
Transistor
as "back to back diodes",
Braitten,
Bardeen and Shockley, Bell Labs, 1949
doping silicon crystal: column 5: phosphorus for n-type, column 3: boron for
p-type
http://hyperphysics.phy-astr.gsu.edu/hbase/solids/dope.html
BJT
thickness 1 micron of base region; emitter more doped than collector;
AZ: electrons moving across E-B junction can diffuse across base
to collector and then move up; a few holes go the opposite direction. See energy
vs distance curve for another POV. What
happens if base is too thick? recombination...
http://www.sp.phy.cam.ac.uk/~SiGe/SiGe%20Heterojunction%20Bipolar%20Transistors%20%28HBTs%29_files/HBTbands.png
http://www.scribd.com/doc/42608819/BJT-Basics
Wikipedia: To
minimize the percentage of carriers that recombine before reaching the collector–base
junction, the transistor's base region must be thin enough that carriers can
diffuse across it in much less time than the semiconductor's minority carrier
lifetime. In particular, the thickness of the base must be much less than the
diffusion length of the electrons.
common emitter inverter; Ic/Ib current gain = 100
emitter follower circuit: a GFI solenoid in the follower.
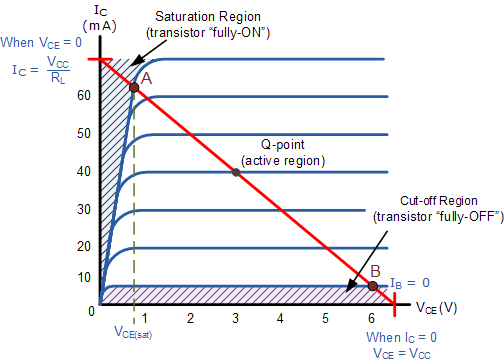
phototransistor
and photons releasing electrons in base.
2N4401 and heat sink.
FETs: better saturation voltage, better freq response. High input impedance.
Horowitz and Hill, The Art of Electronics
----------------
------------------- --------------------- end of Inductors.
(4) Logic, EM spectrum, electrochemistry half cells
ref:
Digital Design from Zero to One, John Wiley & Sons, 1996.
Logic Noise Margins
for
example the TTL (bipolar junction transistor logic family 7400 series)
Vcc the supply voltage is guaranteed between 4.75 and 5.25 v; below 4.75 chips
may not work as advertised; above Vcc-max 7.0 volts chips may be permanently
damaged.
Logic LO = 0 = FALSE = inactive = open switch is between 0v and 0.8v
Logic HI= 1= TRUE = active = closed switch is above 2.2v up to 5.0v
Region in TTL between 0.8 and 2.2 is "not allowed"
Noise
Margin represents the advantage of digital
or analog representation; a digital recording can be faithfully reproduced,
whereas reproduction of an analog "master tape" will always be degraded...
To change from LO to HI the voltage of the TTL logic gate must pass through the noise margin region--as quickly as possible--nanoseconds. An voltage between 0.8 and 2.2 must be "converted" to 0 or 1, from its metastable region. TTL chip mfgrs make chips that have stable outputs only for logic 0 or logic 1... same for any other chip family...
Base
2 numbers, hexidecimal representation: 0 1 2 3 4 5 6 7 8 9 A B C D E F
in base 2, C = 1 1 0 0
in
C++ code for IAR editor hex code is 0xCF = decimal
12*16 + 15 = 207
Combinatorial Logic: logic gates "without memory"
circuits without feedback.
7400
series hex inverters: input hysteresis 7414,
open collector output 7406...interface between voltage levels, drive LEDs...
C
B A OUT
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 0
Realize as "Sum of Products" AND to OR two-level circuit
SEQUENTIAL: logic circuits with memory, with feedback.
Set Reset Latch with output Q
S R Q
0 0 no change: the memory state!
0 1 0 (RESET)
1 0 1 (SET Q to logical 1)
1 1 not allowed!
toggle flip flops
counters
states, and Finite state machines.
CPUs:
instructions: source, function, destination.
Coding, functions, interrupts.
-----------
---------------------- ----------------
Electromagnetic
radiation spectrum:
power lines, radio, microwave/radar, infrared, visible, ultraviolet, x-rays,
gamma rays, cosmic rays.
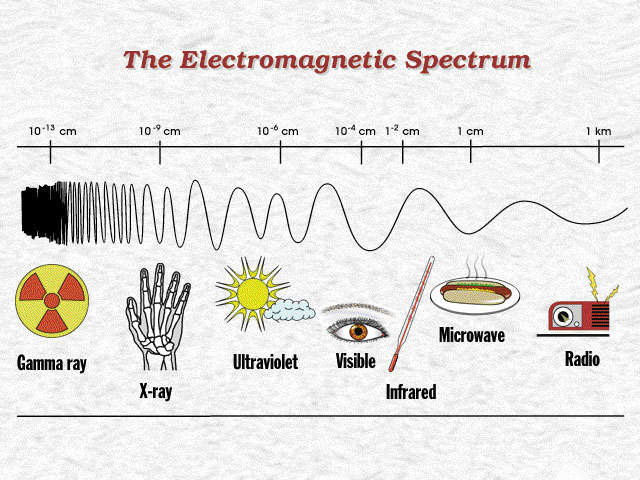
half
cells of electrochemistry
Reference for BMEs:
G. Bendek & F. Villars, Physics with Illustrative Examples from Medicine
and Biology:
vol 3, Electricity and Magnetism