Lab
6: Periodic Waveforms, Sample Rate Aliasing, Fast Fourier Transform & Digital
Filtering (to be done solo)
Background: The
sampling theorem will
be one of the most important constraints you'll learn to work with in instrumentation.
The sampling theorem says if the maximum frequency in the analog input signal is
less than half the sampling rate, you can achieve "perfect reconstruction"
of the input waveform on the digital side. If the max input freq > sampling rate
then aliasing of high frequencies will occur; the aliased frequency is determined
from a "mirror image" formula; an aliased high frequency is a form of
noise.
In this lab you will observe
aliased frequencies. As a prelude, you will learn more about waveform generation,
given our need for periodic signals. Then you will use the Fast Fourier Transform
(FFT) in the 54622A digital 'scope and in LabVIEW's "Power Spectrum" to
demonstrate aliasing in various circumstances.
The 33120A Waveform Generator:
Each setup has the 300-page Users Guide for your study. For this lab we will
care only about the first 3 chapters of the Guide.
Requirements:
See the 8 categories below. For the sake of efficiency, let's say you're prepared
to show us something from each of the 8 sections; we will ask a subset of 3-4
of the items. If you need help, fine, but if the helping takes more than 30
minutes, go off and reread the documentation, then come back the next day...
(1) If asked, you should be
able to display any of the 11 waveforms listed at the top of page 298 (OK,
"DC volts" isn't really a waveform, but you may show it to us anyway,
-see page 24- and realize you have a source of DC signal other than your triple
output power supply. And once in DC=volts, how do you RETURN to sinewave output?).
See page 175 for diagrams of the "built-in arbitrary waveforms". Why
do they call one of the waveforms Cardiac?
(1b) For each of the 9 periodic
waveforms you should be able to change frequency, amplitude and offset.
For pulses, you should understand what Duty Cycle is and show us pulses of 20%
to 80% duty cycle. For any of the parameter changes you should be able to use
the suicide knob, or enter numbers. (See Chpt 1 of the Guide).
1(c) Why is sync called "SYNC"?
What is the use of sync, in conjunction with the o'scope? You should be able
to tell us what's on the SYNC output, on the 33120A front panel. Or show us
on the scope!
(2) Display
noise on the 'scope screen. By turning up the "sample rate" and using
the FFT math function, find out at what (high) frequency the noise amplitude
falls off by half. (hat
tip to Cedric '12)
Become familiar with the Menus
of the 33120A.
(3a) See Chpt 2 of the 33120A documentation. Be able to navigate to Menu D and change
from 50 Ohm to High Z for the output impedance. Show how the amplitude
reading of a waveform changes when you go from 50 ohm to High Z.
(3b) First
create (triggered properly) on the 'scope, from the 33120A function generator,
a 9 cycle burst of square wave pulses at 40KHz rate of amplitude 2v. Make the
burst RATE 400 Hz.
Now have the
burst triggered by the approx 1KHz rising edge from the 54622A scope Probe Comp
output. Ext Trig is an INPUT on the back of 33120A. You should be able to toggle
between the two burst rates...
Don't
connect Probe Comp to Ext Trig with a 10X scope probe... And don't use the
BURST SRC to change to EXT... use a front panel "switch". Note
that on p.100 of the Users Guide it states that pressing the SINGLE button enables
EXT TRIG.
The menu system
under Menu A, items 4, 5, 6, 7, covers relevant burst parameters, including
rate and count. In general, keep away from item 7!
(3c) Be able to use Menu B to
demonstrate a logarithmic sweep of frequencies. Can you trigger a single sweep?
See p. 98 of the 33120A Guide.
(3d) From the waveform generator
to the Digital Multimeter AC volts input arrange that a 1000 Hz sinewave has the
same RMS amplitude (1.00) on both instruments.
(4) Sinewave purity.
Use your Agilent 33120A waveform generator to set up a 2v p-p sinewave,
at 8KHz, and send it on a BNC cable to channel 1 of the 54622A scope. Press
the Math button and highlight the FFT feature. Rotate the time base knob until
the sample rate is 40KHz. Look at the resulting spectrum. Is there a peak at
8KHz? How broad is the peak? Are there any harmonics? (freq's at multiples of
the fundamental--in this case 8KHz). For a cleaner display, suppress the time
base view of the channel 1 signal. Switch to pulse, triangle or sawtooth waveforms
to see more prominent harmonics.
Show the extra
spectrum peaks of a square/triangle/sawtooth waveform. How are the extra peaks
related to the fundamental frequency?
Is the amplitude scale on
the 54622A spectrum log or linear?
(5) Aliasing. Move
the sinewave frequency up, 1000 Hz at a click. Does the spectrum peak shift
as you would expect? Increase
the frequency to 19, 20KHz, then to 21 KHz. At what frequency is 21KHz aliased?
Why is 21KHz aliased? To answer, Recall the Sampling Theorem and be able
to say something about your sample rate... Increase the input frequency up to
39KHz. What is the aliased frequency? What about the alias of 42KHz?
(6) Now try a square wave at lower
frequency, like 6KHz. Increase the fundamental frequency. In the spectrum, can you
make an alias of the first harmonic add with (be equal to...) the fundamental?
(7) Spectrum Analysis in LabVIEW.
Send your 8KHz sinewave into an analog input on the green connector card. Acquire
1 second of the waveform using the AI Acquire Waveform subVI, setting the
sample rate at 40KHz. Use the Power Spectrum subVI from the Analyze:Signal
Processing:Frequency Domain Function Menu. Display the spectrum. Do you see
the same spectrum in LabVIEW that you saw on the digital scope? Be aware that the
amplitude of the spectrum peak may be much less than 1.00!
(8A) Now that you can sample
correctly, lower your sample rate to 400 Hz and send the sample rate to the
sample number input(1 second of sampling). Send the output of
the waveform acquisition to a LP 2nd order Butterworth filter with a
cutoff of 10Hz. Send the output of the DAQ icon and the Butterworth filter to
one Waveform graph. Lower the frequency of the waveform generator to
6, 10, 14 Hz and show filter input vs output. See suggestions below, for showing
the unfiltered and filtered waveforms on the same plot. Build Array on right...
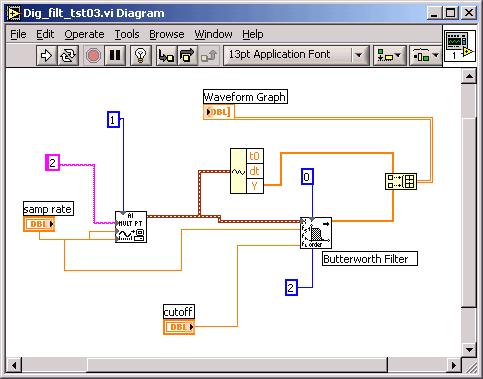
8B: Everything like 8A, except the filter is HIGH
PASS and we see 6 Hz attenuated w.r.t. 14 Hz.
Possible FTQ: Where will be the spectrum peak for a sinewave at a certain
frequency above the Nyquist rate? What's a formula for the frequency where the
fundamental is exactly equal to the alias of its first harmonic?
Further Reading: Visit a National Instruments webpage tutorial
on aliasing here.
