Lab 0.8: Building a LabVIEW array and transferring it to an EXCEL spreadsheet
note: 0.8 is an A-path lab to be done individually, with limited TA troubleshooting
note 2: Lab 0.8 should be completed before attempting Lab LT-A.
Background: You will occasionally need to save particular numbers acquired or computed in LabVIEW. Yes, you can display numbers on indicators and and graphs, but such information disappears when the VI is closed. By transferring numbers from arrays to EXCEL you can have more permanent storage...
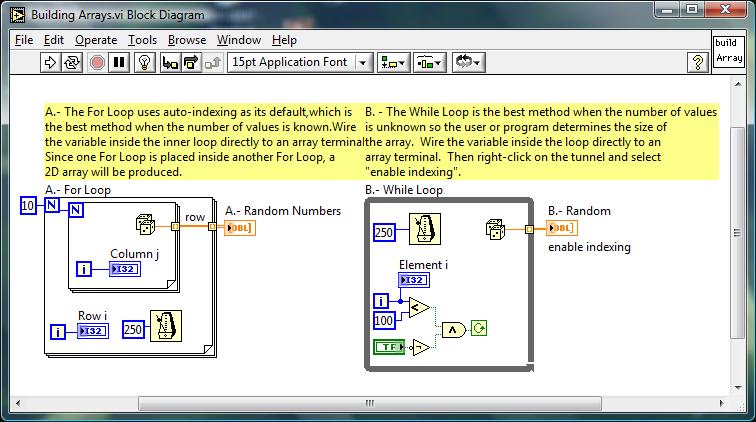
See image below from the
help section of LabVIEW:

Requirements:
A. Create an array of exactly 7 rows by 13 columns on your front panel.
In location (1, 7) place the number 1. "Save current values as default."
To get started building an array go to Front Panel/All
Controls and Array, Matrix, Cluster. Then drag a blank array socket onto the
front panel; fill it with indicators...
Now, using some form of indexed iteration, have LabVIEW automatically fill in rows 2-7 with the start of Pascal's triange. Have your VI wait 2 seconds between rows.
See figure below for what row two would look like.
Once the seven rows are complete, have LabVIEW send the array to an EXCEL spreadsheet. Have the spreadsheet automatically compute (your hand leaves the keyboard and mouse) and fill in the next 4 (non-zero) entries of the middle column--with numbers 2, 6, 20 already there. The next entry after 20 is 70...
You may end up using the matlab xlswrite function inside a Matlab script in your LabVIEW VI.
At any rate, once you start your VI, we will (after about 12 seconds or so) open the spreadsheet (we saw before running the vi) and see the middle column of Pascal's Triangle down to 3432.
Before testing
your VI we will inspect your existing
EXCEL spreadsheet for 0.8 to see that all its cells of interest contain zero.
The "exisiting spreadsheet" will not be deleted and re-crated during
the process of filling it in.
FTQ: We will ask you some question for which Pascal's Triangle will be useful: polynomial coefficients, combinations, probability...minimum unique paths from one corner of a square Manhattan grid to the opposite corner... sum of squares of rows of the triangle...
see http://milan.milanovic.org/math/english/fibo/fibo4.html for a v. large version of the triangle...