Chapter 5

 

Mathematical description of internal forces in solids

 

 

 Our next objective is to outline the mathematical formulas that describe internal and external forces acting on a solid.  Just as there are many different strain measures, there are several different definitions of internal force.  We shall see that internal forces can be described as a second order tensor, which must be symmetric.  Thus, internal forces can always be quantified by a set of six numbers, and the various different definitions are all equivalent.

 

 

<5.1 Surface traction and internal body force

 

Forces can be applied to a solid body in two ways. 

(i) A force can be applied to its boundary: examples include fluid pressure, wind loading, or forces arising from contact with another solid. 

(ii) The solid can be subjected to body forces, which act on the interior of the solid.  Examples include gravitational loading, or electromagnetic forces.

 

 The surface traction vector t at a point on the surface represents the force acting on the surface per unit area of the deformed solid.

 

Formally, let dA be an element of area on a surface.  Suppose that dA is subjected to a force $dP$.  Then

$t=\underset{dA\to 0}{\lim }\frac{dP}{dA}$

The resultant force acting on any portion S of the surface of the deformed solid is

$P={\displaystyle \underset{S}{\int }tdA}$

Surface traction, like `true stress,’ should be thought of as acting on the deformed solid.

 Normal and shear tractions

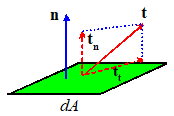
The traction vector is often resolved into components acting normal and tangential to a surface, as shown in the picture. 

 

The normal component is referred to as the normal traction, and the tangential component is known as the shear traction.

 

Formally, let n denote a unit vector normal to the surface.  Then

$t_n=\left(t\cdot n\right)n{t}_t=t-t_n$

 

 

 The body force vector denotes the external force acting on the interior of a solid, per unit mass.

 

Formally, let dV denote an infinitesimal volume element within the deformed solid, and let $\rho$ denote the mass density (mass per unit deformed volume).  Suppose that the element is subjected to a force $dP$.  Then

$b=\frac{1}{\rho }\underset{dV\to 0}{\lim }\frac{dP}{dV}$

The resultant body force acting on any volume V  within the deformed solid is

$P={\displaystyle \underset{V}{\int }\rho bdV}$

 

 

5.2 Traction acting on planes within a solid

 

Every plane in the interior of a solid is subjected to a distribution of traction.  To see this, consider a loaded, solid, body in static equilibrium.  Imagine cutting the solid in two.  The two parts of the solid must each be in static equilibrium.  This is possible only if forces act on the planes that were created by the cut.

 

 The internal traction vector T(n) represents the force per unit area acting on a section of the deformed body across a plane with outer normal vector n.

 

Formally, let dA be an element of area in the interior of the solid, with normal n.  Suppose that the material on the underside of dA is subjected to a force $d{P}^{(n)}$ across the plane dA.  Then

$T(n)=\underset{dA\to 0}{\lim }\frac{d{P}^{(n)}}{dA}$

Note that internal traction is the force per unit area of the deformed solid, like `true stress’

 

 The resultant force acting on any internal volume V with boundary surface A within a deformed solid is

$P={\displaystyle \underset{A}{\int }T(n)dA+}{\displaystyle \underset{V}{\int }\rho bdV}$

The first term is the resultant force acting on the internal surface A, the second term is the resultant body force acting on the interior V.

 

 

 Newton’s third law (every action has an equal and opposite reaction) requires that

$T(-n)=-T(n)$

To see this, note that the forces acting on planes separating two adjacent volume elements in a solid must be equal and opposite.

 

 

 

 Traction acting on different planes passing through the same point are related, in order to satisfy Newton’s second law (F=ma).

 

Let $\left\{e_1,e_2,e_3\right\}$ be a Cartesian basis.  Let $T_i(e_1)$, $T_i(e_2)$, $T_i(e_3)$ denote the components of traction acting on planes with normal vectors in the $e_1$, $e_2$, and $e_3$ directions, respectively.  Then, the traction components $T_i(n)$ acting on a surface with normal n are given by

$T_i(n)=T_i(e_1)n_1+T_i(e_2)n_2+T_i(e_3)n_3$

where $n_i$ are the components of n.

 

To see this, consider the forces acting on the infinitessimal tetrahedron shown in the figure.  The base and sides of the tetrahedron have normals in the $-e_2$, $-e_1$ and $-e_3$ directions.  The fourth face has normal n.  Suppose the volume of the tetrahedron is dV, and let $d{A}_1$,  $d{A}_2$,  $d{A}_3$,  $d{A}_n$ denote the areas of the faces.  Assume that the material within the tetrahedron has mass density $\rho$ and is subjected to a body force b. Let a denote the acceleration of the center of mass of the tetrahedron. Then, F=ma for the tetrahedron requires that

$T(n)d{A}^{(n)}+T(-e_1)d{A}_1+T(-e_2)d{A}_2+T(-e_3)d{A}_3+\rho bdV=\rho dVa$

Recall that $T(-e_i)=-T(e_i)$ and divide through by $d{A}_n$:

$T(n)-T(e_1)\frac{d{A}_1}{d{A}^{(n)}}-T(e_2)\frac{d{A}_2}{d{A}^{(n)}}-T(e_3)\frac{d{A}_3}{d{A}^{(n)}}+\rho b\frac{dV}{d{A}^{(n)}}=\rho \frac{dV}{d{A}^{(n)}}a$

Finally, let $d{A}_n\to 0$.  We can show (see Appendix D) that

$\frac{d{A}_1}{d{A}^{(n)}}=n_1\frac{d{A}_2}{d{A}^{(n)}}=n_2\frac{d{A}_3}{d{A}^{(n)}}=n_3\underset{d{A}^{(n)}\to 0}{\lim }\frac{dV}{d{A}^{(n)}}=0$

so

$T(n)=T(e_1)n_1-T(e_2)n_2-T(e_3)n_3$

or, using index notation

$T_i(n)=T_i(e_1)n_1+T_i(e_2)n_2+T_i(e_3)n_3$

The significance of this result is that the tractions acting on planes with normals in the $e_1$, $e_2$, and $e_3$ directions completely characterize the internal forces that act at a point.  Given these tractions, we can deduce the tractions acting on any other plane.  This leads directly to the definition of the Cauchy stress tensor in the next section.

 

 

5.3 The Cauchy (true) stress tensor

 

Consider a solid which deforms under external loading. Let $\left\{e_1,e_2,e_3\right\}$ be a Cartesian basis.  Let $T_i(e_1)$, $T_i(e_2)$, $T_i(e_3)$ denote the components of traction acting on planes with normals in the $e_1$, $e_2$, and $e_3$ directions, respectively, as outlined in the preceding section 

 

 Define the components of the Cauchy stress tensor  by

$\begin{array}{c}{\sigma }_{ij}=T_j(e_i)\\ \equiv \{\begin{array}{l}{\sigma }_{11}=T_1(e_1){\sigma }_{12}=T_2(e_1){\sigma }_{13}=T_3(e_1)\\ {\sigma }_{21}=T_1(e_2){\sigma }_{22}=T_2(e_2){\sigma }_{23}=T_3(e_2)\\ {\sigma }_{31}=T_1(e_3){\sigma }_{32}=T_2(e_3){\sigma }_{33}=T_3(e_3)\end{array}\end{array}$

Then, the traction  $T_i(n)$ acting on any plane with normal n follows as

$T(n)=n\cdot \sigma \text{or }{T}_i(n)=n_j{\sigma }_{ji}$

 

To see this, recall the last result from the preceding section

$T_i(n)=T_i(e_1)n_1+T_i(e_2)n_2+T_i(e_3)n_3$

and substitute for $T_i(e_j)$ in terms of the components of the Cauchy stress tensor

$T_i(n)={\sigma }_{1i}{n}_1+{\sigma }_{2i}{n}_2+{\sigma }_{3i}{n}_3=n_j{\sigma }_{ji}$

 

The Cauchy stress tensor completely characterizes the internal forces acting in a deformed solid.  The physical significance of the components of the stress tensor is illustrated in the figure: ${\sigma }_{ji}$ represents the ith component of traction acting on a plane with normal in the $e_j$ direction.

 

Note the Cauchy stress represents force per unit area of the deformed solid.  In elementary strength of materials courses it is called `true stress,’ for this reason.

 

HEALTH WARNING: Some texts define stress as the transpose of the definition used here, so that $T(n)=\sigma \cdot n\text{or }{T}_i(n)={\sigma }_{ij}{n}_j$.  In this case the first index for each stress component denotes the direction of traction, while the second denotes the normal to the plane.  We will see later that Cauchy stress is always symmetric, so there is no confusion if you use the wrong definition.  But some stress measures are not symmetric (see below) and in this case you need to be careful to check which convention the author has chosen.

 

 

Example: Consider a state of hydrostatic stress ${\sigma }_{ij}=p{\delta }_{ij}$.  Show that the traction vector acting on any internal plane in the solid (or, more likely, fluid!) has magnitude p and direction normal to the plane.

 

The formula for the traction is

$T_i=n_j{\sigma }_{ji}=n_{j}p{\delta }_{ji}=p{n}_i$

 

where we have used the rules of index notation $a_i={\delta }_{ij}{a}_j$  

 

Example:  A rigid, cubic solid is immersed in a fluid with mass density $\rho$. Recall that a stationary fluid exerts a compressive pressure of magnitude $\rho gh$ at depth h.

 

(a) Write down expressions for the traction vector exerted by the fluid on each face of the cube.  You might find it convenient to take the origin for your coordinate system at the center of the cube, and take basis vectors $\{e_1,e_2,e_3\}$ perpendicular to the cube faces.

 

Let $e_3$ be vertical, and origin at the center of the cube.

• Top face: $t=-\rho gH{e}_3$ 
• Bottom face $t=\rho g(H+2a)e_3$
• Side faces $t=-\rho g(H+a-x_3)e_1,\rho g(H+a-x_3)e_1,-\rho g(H+a-x_3)e_2,\rho g(H+a-x_3)e_2$

 

 

 

(b) Calculate the resultant force due to the tractions acting on the cube, and show that the vertical force is equal and opposite to the weight of fluid displaced by the cube. 

 

The integrals over the side faces are zero (the tractions on opposite faces are equal and opposite).

 

The resultant force of pressure on the top and bottom faces is

$F=\left(-4\rho gH{a}^2+4\rho g(H+2a)a^2\right)e_3=8\rho g{a}^3{e}_3$ 

Example: A rectangular bar is loaded in a state of uniaxial tension, as shown in the figure.

 

(a) Write down the components of the stress tensor in the bar, using the basis vectors shown.

 

The only nonzero component of stress is acting parallel to the $e_2$ direction.   As a matrix, the stress tensor is

$\sigma =\left[\begin{array}{ccc}0& 0& 0\\ 0& \sigma & 0\\ 0& 0& 0\end{array}\right]$

 

(b) Calculate the components of the normal vector to the plane ABCD shown, and hence deduce the components of the traction vector acting on this plane, expressing your answer as components in the basis shown, in terms of $\theta$ 

 

The normal vector is $n=\sin \theta e_1+\cos \theta e_2$ 

It follows that $T=n\cdot \sigma =\left[\begin{array}{ccc}\sin \theta & \cos \theta & 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 0\\ 0& \sigma & 0\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}0& \sigma \cos \theta & 0\end{array}\right]$

 

 

(c) Compute the normal and tangential tractions acting on the plane shown.  What angle maximizes the magnitude of the tangential traction?

 

The normal component of traction is

$T_n=n\cdot T=\sigma {\cos }^2\theta$

The tangential component of traction is therefore

 $\begin{array}{l}\tau =T-T_{n}n=\left[\begin{array}{ccc}0& \sigma \cos \theta & 0\end{array}\right]-\sigma {\cos }^2\theta \left[\begin{array}{ccc}\sin \theta & \cos \theta & 0\end{array}\right]\\ =\left[\begin{array}{ccc}0& \sigma \cos \theta (1-{\cos }^2\theta )& 0\end{array}\right]=\left[\begin{array}{ccc}0& \sigma \cos \theta \sin \theta & 0\end{array}\right]\end{array}$

The magnitude is greatest when $\sigma \cos \theta \sin \theta =(\sigma /2)\sin (2\theta )$ is maximized, i.e. $\theta =\pi /4$ .  The maximum shear traction is $\sigma /2$ .

 

 

 

 

5.4 Other stress measures $–$ Kirchhoff, Nominal and Material stress tensors

 

Cauchy stress ${\sigma }_{ij}$ (the actual force per unit area acting on an actual, deformed solid) is the most physical measure of internal force.  Other definitions of stress often appear in constitutive equations, however. 

 

The other stress measures regard forces as acting on the undeformed solid.  Consequently, to define them we must know not only what the deformed solid looks like, but also what it looked like before deformation.  The deformation is described by a displacement vector $u(x)$ and the associated deformation gradient

$F=I+\nabla u{F}_{ij}={\delta }_{ij}+\frac{\partial u_i}{\partial x_j}$

as outlined in Section 2.1. In addition, let $J=\det (F)$

 

We then define the following stress measures

 

  Kirchhoff stress  $\tau =J\sigma {\tau }_{ij}=J{\sigma }_{ij}$

 Nominal (First Piola-Kirchhoff) stress  $S=J{F}^{-1}\cdot \sigma S_{ij}=J{F}_{ik}^{-1}{\sigma }_{kj}$

 Material (Second Piola-Kirchhoff) stress  $\Sigma =J{F}^{-1}\cdot \sigma \cdot F^{-T}{\Sigma }_{ij}=J{F}_{ik}^{-1}{\sigma }_{kl}{F}_{jl}^{-1}$

 

The inverse relations are also useful $–$ the one for Kirchhoff stress is obvious $–$ the others are

$\sigma =\frac{1}{J}F\cdot S{\sigma }_{ij}=\frac{1}{J}{F}_{ik}{S}_{kj}$               $\sigma =\frac{1}{J}F\cdot \Sigma \cdot F^T{\sigma }_{ij}=\frac{1}{J}{F}_{ik}^{}{\Sigma }_{kl}{F}_{jl}^{}$

 

The Kirchoff stress has no obvious physical significance. 

 

The nominal stress tensor can be regarded as the internal force per unit undeformed area acting within a solid, as follows

1.      Visualize an element of area dA in the deformed solid, with normal n, which is subjected to a force $d{P}^{(n)}$ by the internal traction in the solid;

2.      Suppose that the element of area dA has started out as an element of area $d{A}_0$ with normal $n_0$ in the undeformed solid, as shown in the figure;

3.      Then, the force $d{P}^{(n)}$ is related to the nominal stress by $d{P}_j^{(n)}=d{A}_0{n}_i^0{S}_{ij}$

 

To see this, note that one can show (see Appendix D) that

$dAn=J{F}^{-T}\cdot d{A}_0{n}_{0}dA{n}_i^{}=J{F}_{ki}^{-1}{n}_k^{0}d{A}_0$

Recall that the Cauchy stress is defined so that

$d{P}_i^{(n)}=dA{n}_j{\sigma }_{ji}$

Substituting for $dA{n}_j$ and rearranging shows that

$d{P}_i^{(n)}=Jd{A}_0{n}_k^0\left(F_{kj}^{-1}{\sigma }_{ji}\right)=d{A}_0{n}_k^0{S}_{ki}$

 

The material stress tensor can also be visualized as force per unit undeformed area, except that the forces are regarded as acting within the undeformed solid, rather than on the deformed solid.  Specifically

1.      The infinitesimal force $d{P}^{(n)}$ is assumed to behave like an infinitesimal material fiber in the solid, in the sense that it is stretched and rotated just like an small vector dx in the solid

2.      This means that we can define a (fictitious) force in the reference configuration $d{P}^{(n0)}$ that is related to $d{P}^{(n)}$ by $F\cdot d{P}^{(n0)}=d{P}^{(n)}$ or $F_{ij}d{P}_j{}^{(n0)}=d{P}_i{}^{(n)}$.

3.      This fictitious force is related to material stress by   $d{P}_i^{(n0)}=d{A}_0{n}_j^0{\Sigma }_{ji}$

 

To see this, substitute into the expression relating $d{P}^{(n)}$ to nominal stress to see that

$F_{ik}d{P}_k^{(n0)}=d{A}_0{n}_j^0{S}_{ji}$

Finally multiply through by $F_{li}^{-1}$, note $F_{li}^{-1}{F}_{ik}={\delta }_{lk}$, and rearrange to see that

$d{P}_l^{(n0)}=d{A}_0{n}_j^0{S}_{ji}{F}_{li}^{-1}=d{A}_0{n}_j^0{\Sigma }_{jl}$

where we have noted that ${\Sigma }_{jl}=S_{ji}{F}_{li}^{-1}$

 

In practice, it is best not to try to attach too much physical significance to these stress measures.  Cauchy stress is the best physical measure of internal force $–$ it is the force per unit area acting inside the deformed solid.  The other stress measures are best regarded as generalized forces (in the sense of Lagrangian mechanics), which are work-conjugate to particular strain measures.  This means that the stress measure multiplied by the time derivative of the strain measure tells you the rate of work done by the forces.  When setting up any mechanics problem, we always work with conjugate measures of motion and forces.

 

Specifically, we shall show later that the rate of work $\dot{W}$ done by stresses acting on a small material element with volume $d{V}_0$ in the undeformed solid (and volume $dV$ in the deformed solid) can be computed as

$\dot{W}=D_{ij}{\sigma }_{ij}dV=D_{ij}{\tau }_{ji}d{V}_0={\dot{F}}_{ij}{S}_{ji}d{V}_0={\dot{E}}_{ij}{\Sigma }_{ji}d{V}_0$

where $D_{ij}$ is the stretch rate tensor, ${\dot{F}}_{ij}$ is the rate of change of deformation gradient, and ${\dot{E}}_{ij}$ is the rate of change of Lagrange strain tensor.  Note that Cauchy stress (and also Kirchhoff stress) is not conjugate to any convenient strain measure $–$ this is the main reason that nominal and material stresses need to be defined.  The nominal stress is conjugate to the deformation gradient, while the material stress is conjugate to the Lagrange strain tensor. 

 

Example: An incompressible bar with unstretched length L is stretched to length $\lambda L$ by a uniaxial Cauchy (true) stress $\sigma =\sigma e_1\otimes e_1$ .   Calculate the  nominal stress and material stress in the bar.   Compare the nominal stress with the formula from materials class $S=F/A_0$ 

 

 

From Section 4.5 we know that the deformation gradient is

$\begin{array}{l}{F}_{ij}=\frac{\partial y_i}{\partial x_j}\Rightarrow F_{11}=\lambda F_{22}=F_{33}=\frac{1}{\sqrt{\lambda }}\text{all other }{F}_{ij}=0\\ \Rightarrow F=\left[\begin{array}{ccc}\lambda & 0& 0\\ 0& 1/\sqrt{\lambda }& 0\\ 0& 0& 1/\sqrt{\lambda }\end{array}\right]\end{array}$

We will need the inverse of F, which is (fortunately) easy to find for a diagonal matrix

 

$\Rightarrow F^{-1}=\left[\begin{array}{ccc}1/\lambda & 0& 0\\ 0& \sqrt{\lambda }& 0\\ 0& 0& \sqrt{\lambda }\end{array}\right]$

Note that J=det(F)=1 (as expected, since the deformation is volume preserving)

As a matrix, the Cauchy stress is

$\sigma =\left[\begin{array}{ccc}\sigma & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$

Hence, using the formula, the nominal stress is

$S=J{F}^{-1}\cdot \sigma =\left[\begin{array}{ccc}1/\lambda & 0& 0\\ 0& \sqrt{\lambda }& 0\\ 0& 0& \sqrt{\lambda }\end{array}\right]\left[\begin{array}{ccc}\sigma & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}\lambda \sigma & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$

The material stress is

$\Sigma =J{F}^{-1}\cdot \sigma \cdot F^{-T}=\left[\begin{array}{ccc}\sigma /\lambda & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{ccc}1/\lambda & 0& 0\\ 0& \sqrt{\lambda }& 0\\ 0& 0& \sqrt{\lambda }\end{array}\right]=\left[\begin{array}{ccc}\sigma /{\lambda }^2& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$

 

For comparison, in material class we learn that in uniaxial tension the ‘nominal’ stress is force per unit undeformed area $S=F/A_0$ ; ‘true’ stress is force per unit deformed area $\sigma =F/A$ .  Since the volume of the bar is constant we know that $A\lambda L=A_{0}L\Rightarrow A/A_0=1/\lambda$   So $S=\sigma /\lambda$ , which agrees with the formula that grown-ups use.

 

 

Example: The figure shows the reference and deformed configurations for a solid.  The out-of-plane dimensions are unchanged.  Points a and b are the positions of points A and B after deformation.  The Cauchy stress in the solid is $\sigma m_1\otimes m_1$ .  Determine:

 

 

(a) The components of Cauchy stress in $\{e_1,e_2,e_3\}$

 

We can do this with the basis change formulas for tensors.    The general formula is

$\left[\begin{array}{ccc}{S}_{11}^{(e)}& S_{12}^{(e)}& S_{13}^{(e)}\\ S_{21}^{(e)}& S_{22}^{(e)}& S_{23}^{(e)}\\ S_{31}^{(e)}& S_{32}^{(e)}& S_{33}^{(e)}\end{array}\right]=\left[\begin{array}{l}{m}_1\cdot e_1{m}_2\cdot e_1{m}_3\cdot e_1\\ m_1\cdot e_2{m}_2\cdot e_2{m}_3\cdot e_2\\ m_1\cdot e_3{m}_2\cdot e_3{m}_3\cdot e_3\end{array}\right]\left[\begin{array}{ccc}{S}_{11}^{(m)}& S_{12}^{(m)}& S_{13}^{(m)}\\ S_{21}^{(m)}& S_{22}^{(m)}& S_{23}^{(m)}\\ S_{31}^{(m)}& S_{32}^{(m)}& S_{33}^{(m)}\end{array}\right]\left[\begin{array}{l}{m}_1\cdot e_1{m}_1\cdot e_2{m}_1\cdot e_3\\ m_2\cdot e_1{m}_2\cdot e_2{m}_2\cdot e_3\\ m_3\cdot e_1{m}_3\cdot e_2{m}_3\cdot e_3\end{array}\right]$

Substituting the numbers

$\begin{array}{l}\left[\begin{array}{ccc}{S}_{11}^{(e)}& S_{12}^{(e)}& S_{13}^{(e)}\\ S_{21}^{(e)}& S_{22}^{(e)}& S_{23}^{(e)}\\ S_{31}^{(e)}& S_{32}^{(e)}& S_{33}^{(e)}\end{array}\right]=\left[\begin{array}{l}1/\sqrt{2}-1/\sqrt{2}0\\ 1/\sqrt{2}1/\sqrt{2}0\\ 001\end{array}\right]\left[\begin{array}{ccc}\sigma & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{l}1/\sqrt{2}1/\sqrt{2}0\\ -1/\sqrt{2}1/\sqrt{2}0\\ 001\end{array}\right]\\ =\left[\begin{array}{l}1/\sqrt{2}-1/\sqrt{2}0\\ 1/\sqrt{2}1/\sqrt{2}0\\ 001\end{array}\right]\left[\begin{array}{ccc}\sigma /\sqrt{2}& \sigma /\sqrt{2}& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\\ =\left[\begin{array}{ccc}\sigma /2& \sigma /2& 0\\ \sigma /2& \sigma /2& 0\\ 0& 0& 0\end{array}\right]\end{array}$

 

 

Alternatively we can solve the problem with Dyadic notation

$\sigma m_1\otimes m_1=\frac{1}{2}\sigma (e_1+e_2)\otimes (e_1+e_2)=\frac{1}{2}\sigma e_1\otimes e_1+\frac{1}{2}\sigma \left(e_1\otimes e_2+e_2\otimes e_1\right)+\frac{1}{2}\sigma e_2\otimes e_2$

 

 

 

(b) The components of Nominal stress S in both $\{e_1,e_2,e_3\}$ and $\{m_1,m_2,m_3\}$.   What is the nominal stress in the mixed basis $S_{ij}{e}_i\otimes m_j$ ?

 

 

Recall that by definition $S=J{F}^{-1}\cdot \sigma$

 

We can use the results from HW2:

·         recall $F=RU=VR\Rightarrow F^{-1}=U^{-1}{R}^T=R^T{V}^{-1}$ 

·         recall V has components in $m_1,m_2,m_3$

$\left[\begin{array}{cc}2& 0\\ 0& 1/4\end{array}\right]$

·         R has components

$\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& -1\\ 1& 1\end{array}\right]$

 

Therefore

$R^T{V}^{-1}=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ -1& 1\end{array}\right]\left[\begin{array}{cc}1/2& 0\\ 0& 4\end{array}\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1/2& 4\\ -1/2& 4\end{array}\right]$

 

S follows as

$S=J{F}^{-1}\sigma =\frac{1}{2}\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1/2& 4\\ -1/2& 4\end{array}\right]\left[\begin{array}{cc}\sigma & 0\\ 0& 0\end{array}\right]=\frac{1}{2\sqrt{2}}\left[\begin{array}{cc}\sigma /2& 0\\ -\sigma /2& 0\end{array}\right]$

 

 

We can write this in Dyadic notation as

$\begin{array}{l}S=\frac{\sigma }{4\sqrt{2}}(m_1\otimes m_1-m_2\otimes m_1)\\ =\frac{\sigma }{4\sqrt{2}}\left[\frac{1}{2}(e_1+e_2)\otimes (e_1+e_2)-\frac{1}{2}(-e_1+e_2)\otimes (e_1+e_2)\right]\\ =\frac{\sigma }{4\sqrt{2}}\frac{1}{2}\left[e_1\otimes e_1+e_2\otimes e_2+e_2\otimes e_1+e_1\otimes e_2+e_1\otimes e_1-e_2\otimes e_2-e_1\otimes e_2+e_2\otimes e_1\right]\\ =\frac{\sigma }{4\sqrt{2}}\left[e_1\otimes e_1+e_2\otimes e_1\right]\end{array}$

 

In the mixed basis $S=\frac{\sigma }{4}{e}_1\otimes m_1$ 

 

 

(c)    The components of material stress in both $\{e_1,e_2,e_3\}$ and $\{m_1,m_2,m_3\}$

 

By definition $\Sigma =J{F}^{-1}\sigma F^{-T}=J{R}^T{V}^{-1}\sigma V^{-1}R$ 

 

Note that in the $\{m_1,m_2,m_3\}$ basis

$J{V}^{-1}\sigma V^{-1}=\frac{1}{2}\left[\begin{array}{cc}1/2& 0\\ 0& 4\end{array}\right]\left[\begin{array}{cc}\sigma & 0\\ 0& 0\end{array}\right]\left[\begin{array}{cc}1/2& 0\\ 0& 4\end{array}\right]=\frac{1}{2}\left[\begin{array}{cc}\sigma /4& 0\\ 0& 0\end{array}\right]$ $\equiv \frac{\sigma }{8}{m}_1\otimes m_1$ 

Note also $e_i=R^T{m}_i$ .  Hence

$\Sigma =\frac{\sigma }{8}{e}_1\otimes e_1$ 

 

It follows that

$\Sigma =\frac{\sigma }{8}\frac{1}{2}(m_1-m_2)\otimes (m_1-m_2)=\frac{\sigma }{16}(m_1\otimes m_1+m_1\otimes m_1-m_1\otimes m_2-m_2\otimes m_1)$

 

 

 

5.5 Stress measures for infinitesimal deformations

 

For a problem involving infinitesimal deformation (where shape changes are characterized by the infinitesimal strain tensor and rotation tensor) all the stress measures defined in the preceding section are approximately equal.

${\sigma }_{ij}\approx {\tau }_{ij}\approx S_{ij}\approx {\Sigma }_{ij}$

To see this, write the deformation gradient as $F_{ij}={\delta }_{ij}+\partial u_i/\partial x_j$; recall that $J=\det (F)\approx 1+\partial u_k/\partial x_k$, and finally assume that for infinitesimal motions $\partial u_i/\partial x_j<<1$.  Substituting into the formulas relating Cauchy stress, Nominal stress and Material stress, we see that

${\sigma }_{ij}=\frac{1}{J}{F}_{ik}{S}_{kj}\approx \frac{1}{1+\partial u_p/\partial x_p}\left({\delta }_{ip}+\frac{\partial u_i}{\partial x_p}\right)S_{pj}=S_{pj}+\mathrm{...}\approx S_{pj}$

The same procedure will show that material stress and Cauchy stress are approximately equal, to within a term of order $\partial u_i/\partial x_j<<1$

 

 

5.6 Principal Stresses and directions

 

For any stress measure, the principal stresses ${\sigma }_i$ and their directions $n^{(i)}$, with i=1..3 are defined such that

$n^{(i)}\cdot \sigma ={\sigma }_i{n}^{(i)}\text{or }{n}_j^{(i)}{\sigma }_{jk}={\sigma }_i{n}_k^{(i)}(\text{no sum on }i)$

Clearly,

1. The principal stresses are the (left) eigenvalues of the stress tensor
2. The principal stress directions are the (left) eigenvectors of the stress tensor

 

The term `left’ eigenvector and eigenvalue indicates that the vector multiplies the tensor on the left. We will see later that Cauchy stress and material stress are both symmetric.  For a symmetric tensor the left and right eigenvalues and vectors are the same.

 

Note that the eigenvectors of a symmetric tensor are orthogonal.  Consequently, the principal Cauchy or material stresses can be visualized as tractions acting normal to the faces of a cube. The principal directions specify the orientation of this special cube.

 

One can also show that if ${\sigma }_1>{\sigma }_2>{\sigma }_3$, then ${\sigma }_1$ is the largest normal traction acting on any plane passing through the point of interest, while ${\sigma }_3$ is the lowest.  This is helpful in defining damage criteria for brittle materials, which fail when the stress acting normal to a material plane reaches a critical magnitude.

In the same vein, the largest shear stress can be shown to act on the plane with unit normal vector $m_{\text{shear}}=-(m_1+m_3)/\sqrt{2}$ (at 45^o to the $m_1$ and $m_3$ axes), and its magnitude is ${\tau }_{\text{max}}=\frac{1}{2}({\sigma }_1-{\sigma }_3)$.  This observation is useful for defining yield criteria for metal polycrystals, which begin to deform plastically when the shear stress acting on a material plane reaches a critical value.

 

5.7 Hydrostatic and Deviatoric Stress; von Mises effective stress

 

Given the Cauchy stress tensor $\text{σ}$, the following may be defined:

 

The Hydrostatic stress is defined as ${\sigma }_h=\text{trace(}\sigma )/3\equiv {\sigma }_{kk}/3$

The Deviatoric stress tensor is defined as ${{\sigma }^{\prime }}_{ij}={\sigma }_{ij}-{\sigma }_h{\delta }_{ij}$

The Von-Mises effective stress is defined as ${\sigma }_e=\sqrt{\frac{3}{2}{\sigma }^{\prime }:{\sigma }^{\prime }}=\sqrt{\frac{3}{2}{{\sigma }^{\prime }}_{ij}{{\sigma }^{\prime }}_{ij}}$

 

The hydrostatic stress is a measure of the pressure exerted by a state of stress.  Pressure acts so as to change the volume of a material element.

 

The deviatoric stress is a measure of the shearing exerted by a state of stress. Shear stress tends to distort a solid, without changing its volume.

 

The Von-Mises effective stress can be regarded as a uniaxial equivalent of a multi-axial stress state.  It is used in many failure or yield criteria.  Thus, if a material is known to fail in a uniaxial tensile test (with ${\sigma }_{11}$ the only nonzero stress component) when ${\sigma }_{11}={\sigma }_{crit}$, it will fail when ${\sigma }_e={\sigma }_{crit}$ under multi-axial loading (with several ${\sigma }_{ij}\ne 0$ )

 

The hydrostatic stress and von Mises stress can also be expressed in terms of principal stresses as

$\begin{array}{l}{\sigma }_h=\left({\sigma }_1+{\sigma }_2+{\sigma }_3\right)/3\\ {\sigma }_e=\sqrt{\frac{1}{2}\left\{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2\right\}}\end{array}$

 

The hydrostatic and von Mises stresses are invariants of the stress tensor $–$ they have the same value regardless of the basis chosen to define the stress components.

 

 

 

 

 

 

 

Example: Show that the von-Mises effective stress ${\sigma }_e=\sqrt{\frac{3}{2}{\sigma }^{\prime }:{\sigma }^{\prime }}$  is invariant under a change of basis.

 

 

We have

$\begin{array}{l}{\sigma }^{\prime }=\sigma -trace(\sigma )I/3\\ {\sigma }^{\prime }:{\sigma }^{\prime }=\sigma :\sigma -2trace{(}^{\sigma }/3+trace{(}^{\sigma }/3=\sigma :\sigma -trace{(}^{\sigma }/3\end{array}$

 

We already know that the contraction $\sigma :\sigma$  and trace are invariant, so the von Mises stress must be invariant.

 

In index notation

${\sigma }_e^{(m)}=\sqrt{Q_{ki}{\sigma }_{kl}{Q}_{lj}{Q}_{pi}{\sigma }_{pq}{Q}_{qj}-Q_{ki}{\sigma }_{kl}{Q}_{li}}={\sigma }_e^{(e)}$

 

 

 

 

5.8 Stresses near an external surface or edge $–$ boundary conditions on stresses

 

Note that at an external surface at which tractions are prescribed, some components of stress are known.  Specifically, let n denote a unit vector normal to the surface, and let t denote the traction (force per unit area) acting on the surface.  Then the Cauchy stress at the surface must satisfy

$n_i{\sigma }_{ij}=t_j$

 

For example, suppose that a surface with normal in the $e_2$ direction is subjected to no loading.  Then (noting that $n_i={\delta }_{i2}$ ) it follows that ${\sigma }_{2i}=0$. In addition, two of the principal stress directions must be parallel to the surface; the third (with zero stress) must be perpendicular to the surface.

 

The stress state at an edge is even simpler.  Suppose that surfaces with normals in the $e_2$ and $e_1$ are traction free.  Then ${\sigma }_{1i}={\sigma }_{2i}=0$, so that 6 stress components are known to be zero.