5. Conservation Laws for Continua

 

In this section, we generalize Newton’s laws of motion (conservation of linear and angular momentum); mass conservation; and the laws of thermodynamics for a continuum.

 

 

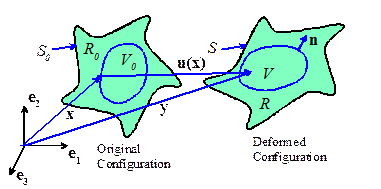
5.1 Mass Conservation

 

The total mass of any subregion within a deformable solid must be conserved.  We can write express this condition as a constraint in several different ways:

 

In integral form:

$\frac{d}{dt}{\displaystyle \underset{V_0}{\int }\rho (X)dV}=\frac{d}{dt}{\displaystyle \underset{V}{\int }\rho (y,t)dV}=\text{0}$

Or, (using Reynolds transport relation) we can write a local mass conservation equation

${\displaystyle \underset{V}{\int }\left({\frac{\partial \rho }{\partial t}|}_{x=const}+\rho \frac{\partial v_i}{\partial y_i}\right)}dV=0\Rightarrow {\frac{\partial \rho }{\partial t}|}_{x=const}+\rho \frac{\partial v_i}{\partial y_i}=0$

 

Alternatively, in spatial form

 

${\frac{\partial \rho }{\partial t}|}_{y=const}+\frac{\partial \rho v_i}{\partial y_i}=0$

 

 

 

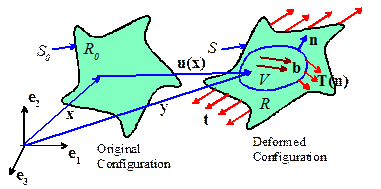5.2 Linear momentum balance in terms of Cauchy stress

 

Let ${\sigma }_{ij}$ denote the Cauchy stress distribution within a deformed solid.  Assume that the solid is subjected to a body force $b_i$, and let $u_i,v_i$ and $a_i$ denote the displacement, velocity and acceleration of a material particle at position $y_i$  in the deformed solid.

 

Newton’s third law of motion (F=ma) can be expressed as

${\nabla }_y\cdot \sigma +\rho b=\rho a\text{ or }\frac{\partial {\sigma }_{ij}}{\partial y_i}+\rho b_j=\rho a_j$

Written out in full

$\begin{array}{l}\frac{\partial {\sigma }_{11}}{\partial y_1}+\frac{\partial {\sigma }_{21}}{\partial y_2}+\frac{\partial {\sigma }_{31}}{\partial y_3}+\rho b_1=\rho a_1\\ \frac{\partial {\sigma }_{12}}{\partial y_1}+\frac{\partial {\sigma }_{22}}{\partial y_2}+\frac{\partial {\sigma }_{32}}{\partial y_3}+\rho b_2=\rho a_2\\ \frac{\partial {\sigma }_{13}}{\partial y_1}+\frac{\partial {\sigma }_{23}}{\partial y_2}+\frac{\partial {\sigma }_{33}}{\partial y_3}+\rho b_3=\rho a_3\end{array}$

Note that the derivative is taken with respect to position in the actual, deformed solid. For the special (but rather common) case of a solid in static equilibrium in the absence of body forces

$\frac{\partial {\sigma }_{ij}}{\partial y_i}=0$

 

Derivation: Recall that the resultant force acting on an arbitrary volume of material V within a solid is

$P_i={\displaystyle \underset{A}{\int }{T}_i(n)dA+}{\displaystyle \underset{V}{\int }\rho b_{i}dV}$

where T(n) is the internal traction acting on the surface A with normal n that bounds V.

 

The linear momentum of the volume V is

${\Lambda }_i={\displaystyle \underset{V}{\int }\rho v_i}dV$

where v is the velocity vector of a material particle in the deformed solid. Express T in terms of ${\sigma }_{ij}$ and set $P_i=d{\Lambda }_i/dt$

${\displaystyle \underset{A}{\int }{\sigma }_{ji}{n}_{j}dA+}{\displaystyle \underset{V}{\int }\rho b_{i}dV}=\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }\rho v_i}dV\right\}$

Apply the divergence theorem to convert the first integral into a volume integral, and note that the Reynolds transport equation implies that

$\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }\rho v_i}dV\right\}={\displaystyle \underset{V}{\int }\rho a_i}dV$

so

${\displaystyle \underset{V}{\int }\frac{\partial {\sigma }_{ji}}{\partial y_j}dV+}{\displaystyle \underset{V}{\int }\rho b_{i}dV}={\displaystyle \underset{V}{\int }\rho a_i}dV\Rightarrow {\displaystyle \underset{V}{\int }\left(\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i-\rho a_i\right)}dV=0$

Since this must hold for every volume of material within a solid, it follows that

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho a_i$

as stated.

 

We can also write this in spatial form by recalling that

$a_i=\frac{\partial v_i}{\partial y_k}{v}_k+{\frac{\partial v_i}{\partial t}|}_{y_i=const}$

so that

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho \left(\frac{\partial v_i}{\partial y_k}{v}_k+{\frac{\partial v_i}{\partial t}|}_{y_i=const}\right)$

 

 

 

5.3 Angular momentum balance in terms of Cauchy stress

 

Conservation of angular momentum for a continuum requires that the Cauchy stress satisfy

${\sigma }_{ji}={\sigma }_{ij}$

i.e. the stress tensor must be symmetric.

 

Derivation: write down the equation for balance of angular momentum for the region V within the  deformed solid

${\displaystyle \underset{A}{\int }y\times TdA}+{\displaystyle \underset{V}{\int }y\times \rho bdV}=\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }y\times \rho vdV}\right\}$

Here, the left hand side is the resultant moment (about the origin) exerted by tractions and body forces acting on a general region within a solid.  The right hand side is the total angular momentum of the solid about the origin.

 

We can write the same expression using index notation

${\displaystyle \underset{A}{\int }{\in }_{ijk}{y}_j{T}_{k}dA}+{\displaystyle \underset{V}{\int }{\in }_{ijk}{y}_j{b}_k\rho dV}=\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }{\in }_{ijk}{y}_j{v}_k\rho dV}\right\}$

Express T in terms of ${\sigma }_{ij}$ and re-write the first integral as a volume integral using the divergence theorem

$\begin{array}{l}{\displaystyle \underset{A}{\int }{\in }_{ijk}{y}_j{T}_{k}dA}={\displaystyle \underset{A}{\int }{\in }_{ijk}{y}_j{\sigma }_{mk}{n}_{m}dA}={\displaystyle \underset{V}{\int }\frac{\partial }{\partial y_m}\left({\in }_{ijk}{y}_j{\sigma }_{mk}\right)dV}\\ ={\displaystyle \underset{V}{\int }{\in }_{ijk}\left({\delta }_{jm}{\sigma }_{mk}+y_j\frac{\partial {\sigma }_{mk}}{\partial x_m}\right)dV}\end{array}$

We may also show that

$\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }{\in }_{ijk}{y}_j{v}_k\rho dV}\right\}={\displaystyle \underset{V}{\int }{\in }_{ijk}{y}_j{a}_k\rho dV}$

Substitute the last two results into the angular momentum balance equation to see that

$\begin{array}{l}{\displaystyle \underset{V}{\int }{\in }_{ijk}\left({\delta }_{jm}{\sigma }_{mk}+y_j\frac{\partial {\sigma }_{mk}}{\partial x_m}\right)dV}+{\displaystyle \underset{V}{\int }{\in }_{ijk}{y}_j{b}_k\rho dV}={\displaystyle \underset{V}{\int }{\in }_{ijk}{y}_j{a}_k\rho dV}\\ \Rightarrow {\displaystyle \underset{V}{\int }{\in }_{ijk}{\delta }_{jm}{\sigma }_{mk}=-}{\displaystyle \underset{V}{\int }{\in }_{ijk}{y}_j\left(\frac{\partial {\sigma }_{mk}}{\partial y_m}+\rho b_k-\rho a_k\right)dV}\end{array}$

The integral on the right hand side of this expression is zero, because the stresses must satisfy the linear momentum balance equation.  Since this holds for any volume V, we conclude that

$\begin{array}{l}{\in }_{ijk}{\delta }_{jm}{\sigma }_{mk}={\in }_{ijk}{\sigma }_{jk}=0\\ \Rightarrow {\in }_{imn}{\in }_{ijk}{\sigma }_{jk}=0\\ \Rightarrow \left({\delta }_{jm}{\delta }_{kn}-{\delta }_{mk}{\delta }_{nj}\right){\sigma }_{jk}=0\\ \Rightarrow {\sigma }_{mn}-{\sigma }_{nm}=0\end{array}$

which is the result we wanted.

 

 

 

5.4 Equations of motion in terms of other stress measures

 

In terms of nominal and material stress the balance of linear momentum is

$\nabla \cdot S+{\rho }_{0}b={\rho }_{0}a\frac{S_{ij}}{\partial x_i}+{\rho }_0{b}_j={\rho }_0{a}_j$

$\nabla \cdot \left[\Sigma \cdot F^T\right]+{\rho }_{0}b={\rho }_{0}a\frac{\partial \left({\Sigma }_{ik}{F}_{jk}\right)}{\partial x_i}+{\rho }_0{b}_j={\rho }_0{a}_j$

Note that the derivatives are taken with respect to position in the undeformed solid.

 

The angular momentum balance equation is

$\begin{array}{l}F\cdot S={\left[F\cdot S\right]}^T\\ \Sigma ={\Sigma }^{{\rm T}}\end{array}$

 

 

To derive these results, you can start with the integral form of the linear momentum balance in terms of Cauchy stress

${\displaystyle \underset{A}{\int }{\sigma }_{ji}{n}_{j}dA+}{\displaystyle \underset{V}{\int }\rho b_{i}dV}=\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }\rho v_i}dV\right\}$

Recall that area elements in the deformed and undeformed solids are related through

$dA{n}_i^{}=J{F}_{ki}^{-1}{n}_k^{0}d{A}_0$

In addition, volume elements are related by $dV=Jd{V}_0$.  We can use these results to re-write the integrals as integrals over a volume in the undeformed solid as

${\displaystyle \underset{A0}{\int }{\sigma }_{ji}J{F}_{kj}^{-1}{n}_k^{0}d{A}_0+}{\displaystyle \underset{V0}{\int }\rho b_{i}Jd{V}_0}=\frac{d}{dt}\left\{{\displaystyle \underset{V0}{\int }\rho v_i}Jd{V}_0\right\}$

Finally, recall that $S_{ij}=J{F}_{ik}^{-1}{\sigma }_{kj}$ and that $J\rho ={\rho }_0$ to see that

${\displaystyle \underset{A0}{\int }S{}_{ki}{n}_k^{0}d{A}_0+}{\displaystyle \underset{V0}{\int }\rho {}_0{b}_{i}d{V}_0}=\frac{d}{dt}\left\{{\displaystyle \underset{V0}{\int }\rho {}_0{v}_i}d{V}_0\right\}$

Apply the divergence theorem to the first term and rearrange

${\displaystyle \underset{V}{\int }\left(\frac{\partial S_{ji}}{\partial x_j}+{\rho }_0{b}_i-{\rho }_0\frac{d{v}_i}{dt}\right)}d{V}_0=0$

Once again, since this must hold for any material volume, we conclude that

$\frac{S_{ij}}{\partial x_i}+{\rho }_0{b}_j={\rho }_0{a}_j$

The linear momentum balance equation in terms of material stress follows directly, by substituting into this equation for $S_{ij}$ in terms of ${\Sigma }_{ij}$

 

The angular momentum balance equation can be derived simply by substituting into the momentum balance equation in terms of Cauchy stress ${\sigma }_{ij}={\sigma }_{ji}$

 

 

 

5.5 Work done by Cauchy stresses

 

Consider a solid with mass density ${\rho }_0$ in its initial configuration, and density $\rho$ in the deformed solid. Let ${\sigma }_{ij}$ denote the Cauchy stress distribution within the solid.  Assume that the solid is subjected to a body force $b_i$ (per unit mass), and let $u_i,v_i$ and $a_i$ denote the displacement, velocity and acceleration of a material particle at position $y_i$  in the deformed solid. In addition, let

$D_{ij}=\frac{1}{2}\left(\frac{\partial v_i}{\partial y_j}+\frac{\partial v_j}{\partial y_i}\right)$

denote the stretch rate in the solid.

 

The rate of work done by Cauchy stresses per unit deformed volume is then ${\sigma }_{ij}{D}_{ij}$.  This energy is either dissipated as heat or stored as internal energy in the solid, depending on the material behavior.

 

We shall show that the rate of work done by internal forces acting on any sub-volume V bounded by a surface A in the deformed solid can be calculated from

$\dot{r}={\displaystyle \underset{A}{\int }{T}_i^{(n)}{v}_{i}dA}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}={\displaystyle \underset{V}{\int }{\sigma }_{ij}{D}_{ij}dV}+\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }\frac{1}{2}\rho v_i{v}_{i}dV}\right\}$

Here, the two terms on the left hand side represent the rate of work done by tractions and body forces acting on the solid (work done = force x velocity).  The first term on the right-hand side can be interpreted as the work done by Cauchy stresses; the second term is the rate of change of kinetic energy. 

 

Derivation: Substitute for $T_i^{(n)}$ in terms of Cauchy stress to see that

$\dot{r}={\displaystyle \underset{A}{\int }{T}_i^{(n)}{v}_{i}dA}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}={\displaystyle \underset{A}{\int }{n}_j{\sigma }_{ji}{v}_{i}dA}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}$

Now, apply the divergence theorem to the first term on the right hand side

$\dot{r}={\displaystyle \underset{V}{\int }\frac{\partial }{\partial y_j}\left({\sigma }_{ji}{v}_i\right)dV}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}$

Evaluate the derivative and collect together the terms involving body force and stress divergence

$\dot{r}={\displaystyle \underset{V}{\int }\left\{{\sigma }_{ji}\frac{\partial v_i}{\partial y_j}+\left(\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i\right)v_i\right\}dV}$

Recall the equation of motion

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho a_i$

and note that since the stress is symmetric ${\sigma }_{ij}={\sigma }_{ji}$

${\sigma }_{ji}\frac{\partial v_i}{\partial y_j}=\frac{1}{2}\left({\sigma }_{ij}+{\sigma }_{ji}\right)\frac{\partial v_i}{\partial y_j}=\frac{1}{2}{\sigma }_{ij}\left(\frac{\partial v_i}{\partial y_j}+\frac{\partial v_j}{\partial y_i}\right)={\sigma }_{ij}{D}_{ij}$

to see that

$\dot{r}={\displaystyle \underset{V}{\int }\left\{{\sigma }_{ij}{D}_{ij}+\rho a_i{v}_i\right\}dV}$

Finally, note that

$\begin{array}{l}{\displaystyle \underset{V}{\int }\rho a_i{v}_{i}dV}={\displaystyle \underset{V_0}{\int }{\rho }_o\frac{d{v}_i}{dt}{v}_{i}d{V}_0=}{\displaystyle \underset{V_0}{\int }{\rho }_o\frac{1}{2}\frac{d}{dt}\left(v_i{v}_i\right)d{V}_0}\\ =\frac{d}{dt}\left({\displaystyle \underset{V_0}{\int }\frac{1}{2}{\rho }_0\left(v_i{v}_i\right)d{V}_0}\right)=\frac{d}{dt}\left({\displaystyle \underset{V_0}{\int }\frac{1}{2}{\rho }_0\left(v_i{v}_i\right)d{V}_0}\right)=\frac{d}{dt}{\displaystyle \underset{V_{}}{\int }\frac{1}{2}\rho \left(v_i{v}_i\right)dV}\end{array}$

Finally, substitution leads to

$\dot{r}={\displaystyle \underset{A}{\int }{T}_i^{(n)}{v}_{i}dA}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}={\displaystyle \underset{V}{\int }{\sigma }_{ij}{D}_{ij}dV}+\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }\frac{1}{2}\rho v_i{v}_{i}dV}\right\}$

as required.

 

 

5.6 Rate of mechanical work in terms of other stress measures

 

 The rate of work done per unit undeformed volume by Kirchhoff stress is ${\tau }_{ij}{D}_{ij}$

 The rate of work done per unit undeformed volume by Nominal stress is $S_{ij}{\dot{F}}_{ji}$

 The rate of work done per unit undeformed volume by Material stress is ${\Sigma }_{ij}{\dot{E}}_{ij}$

 

This shows that nominal stress and deformation gradient are work conjugate, as are material stress and Lagrange strain.

 

In addition, the rate of work done on a volume $V_0$ of the undeformed solid can be expressed as

$\dot{r}={\displaystyle \underset{A}{\int }{T}_i^{(n)}{v}_{i}dA}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}={\displaystyle \underset{V_0}{\int }{\tau }_{ij}{D}_{ij}d{V}_0}+\frac{d}{dt}\left\{{\displaystyle \underset{V_0}{\int }\frac{1}{2}{\rho }_0{v}_i{v}_{i}d{V}_0}\right\}$

$\dot{r}={\displaystyle \underset{A}{\int }{T}_i^{(n)}{v}_{i}dA}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}={\displaystyle \underset{V_0}{\int }{S}_{ij}{\dot{F}}_{ji}d{V}_0}+\frac{d}{dt}\left\{{\displaystyle \underset{V_0}{\int }\frac{1}{2}{\rho }_0{v}_i{v}_{i}d{V}_0}\right\}$

$\dot{r}={\displaystyle \underset{A}{\int }{T}_i^{(n)}{v}_{i}dA}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}={\displaystyle \underset{V_0}{\int }{\Sigma }_{ij}{\dot{E}}_{ij}d{V}_0}+\frac{d}{dt}\left\{{\displaystyle \underset{V_0}{\int }\frac{1}{2}{\rho }_0{v}_i{v}_{i}d{V}_0}\right\}$

 

Derivations: The proof of the first result (and the stress power of Kirchhoff stress) is straightforward and is left as an exercise.  To show the second result, note that $T_i^{(n)}dA=n_j^0{S}_{ji}d{A}_0$ and $dV=Jd{V}_0$ to re-write the integrals over the undeformed solid; then and apply the divergence theorem to see that

$\dot{r}={\displaystyle \underset{V_0}{\int }\frac{\partial }{\partial x_j}\left(S_{ji}{v}_i\right)d{V}_0}+{\displaystyle \underset{V0}{\int }\rho b_i{v}_{i}Jd{V}_0}$

Evaluate the derivative, recall that $J\rho ={\rho }_0$ and use the equation of motion

$\frac{S_{ij}}{\partial x_i}+{\rho }_0{b}_j={\rho }_0\frac{d{v}_j}{dt}$

to see that

$\dot{r}={\displaystyle \underset{V_0}{\int }{S}_{ji}\frac{\partial v_i}{\partial x_j}d{V}_0}+{\displaystyle \underset{V0}{\int }{\rho }_0\frac{d{v}_i}{dt}{v}_{i}d{V}_0}$

Finally, note that $\partial v_i/\partial x_j=\left(\partial {\dot{u}}_i/\partial x_j\right)={\dot{F}}_{ij}$ and re-write the second integral as a kinetic energy term as before to obtain the required result.

 

The third result follows by straightforward algebraic manipulations $–$ note that by definition

$S_{ij}{\dot{F}}_{ji}={\Sigma }_{ik}{F}_{jk}^{}{\dot{F}}_{ji}$

Since ${\Sigma }_{ij}$ is symmetric it follows that

${\Sigma }_{ik}{F}_{jk}^{}{\dot{F}}_{ji}=\frac{1}{2}\left({\Sigma }_{ik}+{\Sigma }_{ki}\right)F_{jk}^{}{\dot{F}}_{ji}={\Sigma }_{ik}\frac{1}{2}\left(F_{jk}^{}{\dot{F}}_{ji}+F_{ji}^{}{\dot{F}}_{jk}\right)={\Sigma }_{ik}{\dot{E}}_{ik}$

 

5.7 Rate of mechanical work for infinitesimal deformations

 

For infintesimal motions all stress measures are equal; and all strain rate measures can be approximated by the infinitesimal strain tensor $\epsilon$.  The rate of work done by stresses per unit volume of either deformed or undeformed solid (the difference is neglected) can be expressed as ${\sigma }_{ij}{\dot{\epsilon }}_{ij}$, and the work done on a volume $V_0$ of the solid is

$\dot{r}={\displaystyle \underset{A}{\int }{T}_i^{(n)}{v}_{i}dA}+{\displaystyle \underset{V}{\int }\rho b_i{v}_{i}dV}={\displaystyle \underset{V_0}{\int }{\sigma }_{ij}{\dot{\epsilon }}_{ij}d{V}_0}+\frac{d}{dt}\left\{{\displaystyle \underset{V_0}{\int }\frac{1}{2}{\rho }_0{v}_i{v}_{i}d{V}_0}\right\}$

 

 

5.8 The principle of Virtual Work

 

The principle of virtual work forms the basis for the finite element method in the mechanics of solids and so will be discussed in detail in this section.

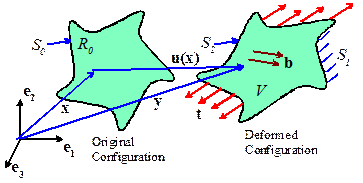
Suppose that a deformable solid is subjected to loading that induces a displacement field $u(x)$, and a velocity field $v(x)$.  The loading consists of a prescribed displacement on part of the boundary (denoted by $S_1$ ), together with a traction t (which may be zero in places) applied to the rest of the boundary (denoted by $S_2$ ).  The loading induces a Cauchy stress ${\sigma }_{ij}$.  The stress field satisfies the angular momentum balance equation ${\sigma }_{ij}={\sigma }_{ji}$.

 

The principle of virtual work is a different way of re-writing partial differential equation for linear moment balance

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho \frac{d{v}_i}{dt}$

in an equivalent integral form, which is much better suited for computer solution.

 

To express the principle, we define a kinematically admissible virtual velocity field $\delta v(y)$, satisfying  $\delta v=0$ on $S_1$.  You can visualize this field as a small change in the velocity of the solid, if you like, but it is really just an arbitrary differentiable vector field.  The term `kinematically admissible’ is just a complicated way of saying that the field is continuous, differentiable, and satisfies $\delta v=0$ on $S_1$ - that is to say, if you perturb the velocity by $\delta v(y)$, the boundary conditions on displacement are still satisfied.

 

In addition, we define an associated virtual velocity gradient, and virtual stretch rate as

$\delta L_{ij}=\frac{\partial \delta v_i}{\partial y_j}\delta D_{ij}=\frac{1}{2}\left(\frac{\partial \delta v_i}{\partial y_j}+\frac{\partial \delta v_j}{\partial y_i}\right)$

 

The principal of virtual work may be stated in two ways.

 

First version of the principle of virtual work

 

The first is not very interesting, but we will state it anyway.  Suppose that the Cauchy stress satisfies:

1.      The boundary condition $n_i{\sigma }_{ij}=t_j$ on $S_2$

2.      The linear momentum balance equation

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho \frac{d{v}_i}{dt}$

Then the virtual work equation

${\displaystyle \underset{V}{\int }{\sigma }_{ij}\delta D_{ij}dV+{\displaystyle \underset{V}{\int }\rho \frac{d{v}_i}{dt}\delta v_i}dV-{\displaystyle \underset{V}{\int }\rho b_i\delta v_{i}dV-{\displaystyle \underset{S_2}{\int }{t}_i\delta v_i}}}dA=0$

is satisfied for all virtual velocity fields.

 

Proof:  Observe that since the Cauchy stress is symmetric

${\sigma }_{ij}\delta D_{ij}=\frac{1}{2}{\sigma }_{ij}\left(\frac{\partial \delta v_i}{\partial y_j}+\frac{\partial \delta v_j}{\partial y_i}\right)=\frac{1}{2}\left({\sigma }_{ji}\frac{\partial \delta v_i}{\partial y_j}+{\sigma }_{ij}\frac{\partial \delta v_j}{\partial y_i}\right)={\sigma }_{ji}\frac{\partial \delta v_i}{\partial y_j}$

Next, note that

${\sigma }_{ji}\frac{\partial v_i}{\partial y_j}=\frac{\partial }{\partial y_j}\left({\sigma }_{ji}\delta v_i\right)-\frac{\partial {\sigma }_{ji}}{\partial y_j}\delta v_i$

Finally, substituting the latter identity into the virtual work equation, applying the divergence theorem, using the linear momentum balance equation and boundary conditions on $\sigma$ and $\delta v(y)$ we obtain the required result.

 

Second version of the principle of virtual work

 

The converse of this statement is much more interesting and useful.  Suppose that ${\sigma }_{ij}$ satisfies the virtual work equation

${\displaystyle \underset{V}{\int }{\sigma }_{ij}\delta D_{ij}dV+{\displaystyle \underset{V}{\int }\rho \frac{d{v}_i}{dt}\delta v_i}dV-{\displaystyle \underset{V}{\int }\rho b_i\delta v_{i}dV-{\displaystyle \underset{S_2}{\int }{t}_i\delta v_i}}}dA=0$

for all virtual velocity fields $\delta v(y)$.  Then the stress field must satisfy

3.      The boundary condition $n_i{\sigma }_{ij}=t_j$ on $S_2$

4.      The linear momentum balance equation

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho \frac{d{v}_i}{dt}$

The significance of this result is that it gives us an alternative way to solve for a stress field that satisfies the linear momentum balance equation, which avoids having to differentiate the stress.  It is not easy to differentiate functions accurately in the computer, but it is easy to integrate them.  The virtual work statement is the starting point for any finite element solution involving deformable solids.

 

 

 

 

Proof: Follow the same preliminary steps as before, i..e.

${\sigma }_{ij}\delta D_{ij}=\frac{1}{2}{\sigma }_{ij}\left(\frac{\partial \delta v_i}{\partial y_j}+\frac{\partial \delta v_j}{\partial y_i}\right)=\frac{1}{2}\left({\sigma }_{ji}\frac{\partial \delta v_i}{\partial y_j}+{\sigma }_{ij}\frac{\partial \delta v_j}{\partial y_i}\right)={\sigma }_{ji}\frac{\partial \delta v_i}{\partial y_j}$

${\sigma }_{ji}\frac{\partial v_i}{\partial y_j}=\frac{\partial }{\partial y_j}\left({\sigma }_{ji}\delta v_i\right)-\frac{\partial {\sigma }_{ji}}{\partial y_j}\delta v_i$

and substitute into the virtual work equation

${\displaystyle \underset{V}{\int }\left\{\frac{\partial }{\partial y_j}\left({\sigma }_{ji}\delta v_i\right)-\frac{\partial {\sigma }_{ji}}{\partial y_j}\delta v_i\right\}dV+{\displaystyle \underset{V}{\int }\rho \frac{d{v}_i}{dt}\delta v_i}dV-{\displaystyle \underset{V}{\int }\rho b_i\delta v_{i}dV-{\displaystyle \underset{S_2}{\int }{t}_i\delta v_i}}}dA=0$

Apply the divergence theorem to the first term in the first integral, and recall that $\delta v=0$ on $S_1$, we see that

$-{\displaystyle \underset{V}{\int }\left\{\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i-\rho \frac{d{v}_i}{dt}\right\}\delta v_{i}dV}+{\displaystyle \underset{S_2}{\int }\left({\sigma }_{ji}{n}_j-t_i\right)\delta v_i}dA=0$

Since this must hold for all virtual velocity fields we could choose

$\delta v_i=f(y)\left\{\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i-\rho \frac{d{v}_i}{dt}\right\}$

where $f(y)=0$ is an arbitrary function that is positive everywhere inside the solid, but is equal to zero on $S$.  For this choice, the virtual work equation reduces to

$-{\displaystyle \underset{V}{\int }f\left(y\right)\left\{\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i-\rho \frac{d{v}_i}{dt}\right\}\left\{\frac{\partial {\sigma }_{ki}}{\partial y_k}+\rho b_i-\rho \frac{d{v}_i}{dt}\right\}dV}=0$

and since the integrand is positive everywhere the only way the equation can be satisfied is if

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho \frac{d{v}_i}{dt}$

Given this, we can next choose a virtual velocity field that satisfies

$\delta v_i=\left({\sigma }_{ji}{n}_j-t_i\right)$

on $S_2$.  For this choice (and noting that the volume integral is zero) the virtual work equation reduces to

$+{\displaystyle \underset{S_2}{\int }\left({\sigma }_{ji}{n}_j-t_i\right)\left({\sigma }_{ki}{n}_k-t_i\right)}dA=0$

Again, the integrand is positive everywhere (it is a perfect square) and so can vanish only if

${\sigma }_{ji}{n}_j=t_i$

as stated.

 

 

5.9 The Virtual Work equation in terms of other stress measures.

 

It is often convenient to implement the virtual work equation in a finite element code using different stress measures. 

 

To do so, we define

1.      The actual deformation gradient in the solid $F_{ij}={\delta }_{ij}+\frac{\partial u_i}{\partial x_j}$

2.      The virtual rate of change of deformation gradient  $\delta {\dot{F}}_{ij}=\frac{\partial \delta v_i}{\partial y_k}{F}_{kj}=\frac{\partial \delta v_i}{\partial x_j}$

3.      The virtual rate of change of Lagrange strain $\delta {\dot{E}}_{ij}=\frac{1}{2}\left(F_{ki}\delta {\dot{F}}_{kj}+\delta {\dot{F}}_{ki}{F}_{kj}\right)$

In addition, we define (in the usual way)

1.      Kirchhoff stress  ${\tau }_{ij}=J{\sigma }_{ij}$

2.      Nominal (First Piola-Kirchhoff) stress  $S_{ij}=J{F}_{ik}^{-1}{\sigma }_{kj}$

3.      Material (Second Piola-Kirchhoff) stress  ${\Sigma }_{ij}=J{F}_{ik}^{-1}{\sigma }_{kl}{F}_{jl}^{-1}$

 

In terms of these quantities, the virtual work equation may be expressed as

${\displaystyle \underset{V0}{\int }{\tau }_{ij}\delta D_{ij}d{V}_0+{\displaystyle \underset{V_0}{\int }{\rho }_0\frac{d{v}_i}{dt}\delta v_i}d{V}_0-{\displaystyle \underset{V0}{\int }{\rho }_0{b}_i\delta v_{i}d{V}_0-{\displaystyle \underset{S_2}{\int }{t}_i\delta v_i}}}dA=0$

${\displaystyle \underset{V0}{\int }{S}_{ij}\delta {\dot{F}}_{ji}d{V}_0+{\displaystyle \underset{V_0}{\int }{\rho }_0\frac{d{v}_i}{dt}\delta v_i}d{V}_0-{\displaystyle \underset{V0}{\int }{\rho }_0{b}_i\delta v_{i}d{V}_0-{\displaystyle \underset{S_2}{\int }{t}_i\delta v_i}}}dA=0$

${\displaystyle \underset{V0}{\int }{\Sigma }_{ij}\delta {\dot{E}}_{ij}d{V}_0+{\displaystyle \underset{V_0}{\int }{\rho }_0\frac{d{v}_i}{dt}\delta v_i}d{V}_0-{\displaystyle \underset{V0}{\int }{\rho }_0{b}_i\delta v_{i}d{V}_0-{\displaystyle \underset{S_2}{\int }{t}_i\delta v_i}}}dA=0$

Note that all the volume integrals are now taken over the undeformed solid $–$ this is convenient for computer applications, because the shape of the undeformed solid is known.  The area integral is evaluated over the deformed solid, unfortunately.  It can be expressed as an equivalent integral over the undeformed solid, but the result is messy and will be deferred until we actually need to do it.

 

5.10 The Virtual Work equation for infinitesimal deformations.

 

For infintesimal motions, the Cauchy, Nominal, and Material stress tensors are equal; and the virtual stretch rate can be replaced by the virtual infinitesimal strain rate

$\delta {\dot{\epsilon }}_{ij}=\frac{1}{2}\left(\frac{\partial \delta v_i}{\partial x_j}+\frac{\partial \delta v_j}{\partial x_i}\right)$

There is no need to distinguish between the volume or surface area of the deformed and undeformed solid.  The virtual work equation can thus be expressed as

${\displaystyle \underset{V0}{\int }{\sigma }_{ij}\delta {\dot{\epsilon }}_{ij}d{V}_0+{\displaystyle \underset{V_0}{\int }{\rho }_0\frac{d{v}_i}{dt}\delta v_i}d{V}_0-{\displaystyle \underset{V0}{\int }{\rho }_0{b}_i\delta v_{i}d{V}_0-{\displaystyle \underset{S_2}{\int }{t}_i\delta v_i}}}d{A}_0=0$

for all kinematically admissible velocity fields.

 

 

As a special case, this expression can be applied to a quasi-static state with $v_i=0$. Then, for a stress state ${\sigma }_{ij}$ satisfying the static equilibrium equation ${\sigma }_{ij}/d{x}_i+{\rho }_0{b}_j=0$ and boundary conditions ${\sigma }_{ij}{n}_j=t_i$ on $S_2$, the virtual work equation reduces to

${\displaystyle \underset{V0}{\int }{\sigma }_{ij}\delta {\epsilon }_{ij}d{V}_0}={\displaystyle \underset{V0}{\int }{\rho }_0{b}_i\delta u_{i}d{V}_0+{\displaystyle \underset{S_2}{\int }{t}_i\delta u_{i}dA}}$

In which $\delta u_i$ are kinematically admissible displacements components $(\delta u_i=0$ on S₂) and $\delta {\epsilon }_{ij}=\left(\partial \delta u_i/x_j+\partial \delta u_j/x_i\right)/2$.

 

Conversely, if  the stress state ${\sigma }_{ij}$ satisfies ${\displaystyle \underset{V0}{\int }{\sigma }_{ij}\delta {\epsilon }_{ij}d{V}_0}={\displaystyle \underset{V0}{\int }{\rho }_0{b}_i\delta u_{i}d{V}_0+{\displaystyle \underset{S_2}{\int }{t}_i\delta u_{i}dA}}$ for every set of kinematically admissible virtual displacements, then the stress state ${\sigma }_{ij}$ satisfies the static equilibrium equation ${\sigma }_{ij}/d{x}_i+{\rho }_0{b}_j=0$ and boundary conditions ${\sigma }_{ij}{n}_j=t_i$ on $S_2$.

 

 

5.10 The first and second laws of thermodynamics for continua 

 

 

Consider a sub-region V of a deformed solid with surface A.   Define:

 The heat flux vector q , which is defined so that $dQ=q\cdot ndA$ is the heat flux crossing an internal surface with area dA and normal n in the deformed solid;

 The heat supply q , defined so that dQ= qdV is the heat supplied from an external source into a volume element dV in the deformed solid;

 The net heat flux into the solid $Q={\displaystyle \underset{V}{\int }qdV}-{\displaystyle \underset{A}{\int }q\cdot ndA}$

  The net rate of mechanical work done on the solid $W={\displaystyle \underset{V}{\int }b\cdot v}dV+{\displaystyle \underset{A}{\int }n\cdot \sigma }\cdot vdA$

  The total kinetic energy $KE={\displaystyle \underset{V}{\int }\frac{1}{2}\rho (v_i{v}_i)dV}$

  The total internal energy ${\rm E}={\displaystyle \underset{V}{\int }\rho \epsilon dV}$ where $\epsilon$ is the specific internal energy (internal energy per unit mass)

  The total entropy $S={\displaystyle \underset{V}{\int }\rho sdV}$, where $s$ is the specific entropy (entropy per unit mass)

  The temperature of the solid $\theta$.

  The net external entropy supplied to the volume $\frac{d{\rm H}}{dt}={\displaystyle \underset{A}{\int }-\frac{q}{\theta }\cdot ndA}+{\displaystyle \underset{V}{\int }\frac{q}{\theta }dV}$

  The specific free energy $\psi =\epsilon -\theta s$

  The total free energy $\Psi ={\displaystyle \underset{V}{\int }\rho \psi dV}$

 

The first law of thermodynamics then requires that

$\frac{d}{dt}({\rm E}+KE)=Q+W$

for any volume V.  

 

This condition can also be expressed as

$\rho {\frac{\partial \epsilon }{\partial t}|}_{x=const}={\sigma }_{ij}{D}_{ij}-\frac{\partial q_i}{\partial y_i}+q$

 

To see this,

1. recall that

$W={\displaystyle \underset{V}{\int }{b}_i{v}_i}dV+{\displaystyle \underset{A}{\int }{\sigma }_{ij}{n}_i{v}_j}dA={\displaystyle \underset{V}{\int }{\sigma }_{ij}{D}_{ij}dV}+\frac{d}{dt}\left\{{\displaystyle \underset{V}{\int }\frac{1}{2}\rho v_i{v}_{i}dV}\right\}={\displaystyle \underset{V}{\int }{\sigma }_{ij}{D}_{ij}dV}+\frac{d}{dt}(KE)$

2. the divergence theorem gives

$Q={\displaystyle \underset{V}{\int }qdV}-{\displaystyle \underset{A}{\int }q\cdot ndA}={\displaystyle \underset{V}{\int }\left(q-\frac{\partial q_i}{\partial y_i}\right)dV}$

3. Therefore

$\frac{d}{dt}\left({\displaystyle \underset{V}{\int }\rho \epsilon dV}+KE\right)={\displaystyle \underset{V}{\int }\left(q-\frac{\partial q_i}{\partial y_i}\right)dV}+{\displaystyle \underset{V}{\int }{\sigma }_{ij}{D}_{ij}dV}+\frac{d}{dt}(KE)$

4. Note also that

$\frac{d}{dt}{\displaystyle \underset{V}{\int }\rho \epsilon dV}=\frac{d}{dt}{\displaystyle \underset{V_0}{\int }{\rho }_0\epsilon dV}={\displaystyle \underset{V_0}{\int }{\rho }_0\frac{d\epsilon }{dt}dV}={\displaystyle \underset{V}{\int }\rho \frac{d\epsilon }{dt}dV}$

where ${\rho }_0=J\rho$ is the mass density per unit reference volume.  Finally

${\displaystyle \underset{V}{\int }\rho \frac{d\epsilon }{dt}dV}={\displaystyle \underset{V}{\int }\left(q-\frac{\partial q_i}{\partial y_i}\right)dV}+{\displaystyle \underset{V}{\int }{\sigma }_{ij}{D}_{ij}dV}$

This must hold for all V, giving the required result.

 

 

The second law of thermodynamics specifies that the net entropy production within V must be non-negative, i.e.

$\frac{dS}{dt}-\frac{d{\rm H}}{dt}\ge 0$

This can also be expressed as

$\rho \frac{\partial s}{\partial t}+\frac{\partial (q_i/\theta )}{\partial y_i}-\frac{q}{\theta }\ge 0$

(this condition is know as the Clausius-Duhem inequality).

 

To see this, simply substitute the definitions and use the divergence theorem.

 

 

The first and second laws can be combined to yield the free energy imbalance

 

${\sigma }_{ij}{D}_{ij}-\frac{1}{\theta }{q}_i\frac{\partial \theta }{\partial y_i}-\rho \left(\frac{\partial \psi }{\partial t}+s\frac{\partial \theta }{\partial t}\right)\ge 0$

 

This can also be expressed as

$W-\frac{d(KE)}{dt}-\frac{d\Psi }{dt}-{\displaystyle \underset{V}{\int }\left(\rho s\frac{\partial \theta }{\partial t}+\frac{1}{\theta }{q}_i\frac{\partial \theta }{\partial y_i}\right)dV}\ge 0$

 

To see the first result,

1. note that

$\rho \frac{\partial s}{\partial t}+\frac{\partial (q_i/\theta )}{\partial y_i}-\frac{q}{\theta }=\rho \frac{\partial s}{\partial t}+\frac{1}{\theta }\frac{\partial q_i}{\partial y_i}-\frac{q}{\theta }-\frac{1}{{\theta }^2}{q}_i\frac{\partial \theta }{\partial y_i}$

2. Use the first law to see that

$\begin{array}{l}\rho \frac{\partial s}{\partial t}+\frac{1}{\theta }\frac{\partial q_i}{\partial y_i}-\frac{q}{\theta }-\frac{1}{{\theta }^2}{q}_i\frac{\partial \theta }{\partial y_i}=\rho \frac{\partial s}{\partial t}+\frac{1}{\theta }\left(-\rho {\frac{\partial \epsilon }{\partial t}|}_{x=const}+{\sigma }_{ij}{D}_{ij}\right)-\frac{1}{{\theta }^2}{q}_i\frac{\partial \theta }{\partial y_i}\ge 0\\ \Rightarrow {\sigma }_{ij}{D}_{ij}-\rho \frac{\partial }{\partial t}(\psi +\theta s)+\theta \rho \frac{\partial s}{\partial t}-\frac{1}{\theta }{q}_i\frac{\partial \theta }{\partial y_i}\ge 0\end{array}$

where we have noted that temperature is always positive.  This yields the solution.

 

The second result follows by integrating the local form and using the stress-power work expression.

 

 

 

 

 

 

 

5.11 Conservation laws for a control volume

 

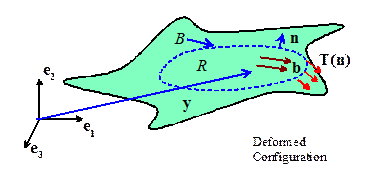To model solids, it is usually convenient to write the equations of motion for a volume that moves with the solid.   When modeling fluids, it is often preferable to consider a fixed spatial volume, through which the fluid moves with time.   To this end,

 We consider a fixed region in space R, bounded by a surface B.  

 Material flows through the region with velocity field v(y,t).

 The solid has mass density per unit deformed volume (in the spatial configuration) $\rho$; and is subjected to a body force b per unit mass. 

 A heat flux q flows through the solid; while an external source injects heat flux Q per unit deformed volume.

 

The conservation laws can be expressed in terms of integrals over the fixed spatial region (which does not move with the solid) as follows

 

Mass Conservation: $\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho dV}+{\displaystyle \underset{B}{\int }\rho v\cdot ndA}=0$

Linear Momentum Balance ${\displaystyle \underset{B}{\int }n\cdot \sigma dA}+{\displaystyle \underset{R}{\int }\rho bdV}=\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho v}dV+{\displaystyle \underset{B}{\int }(\rho v)v\cdot ndA}$

Angular Momentum Balance ${\displaystyle \underset{B}{\int }y\times (n\cdot \sigma )dA}+{\displaystyle \underset{R}{\int }y\times (\rho b)dA}=\frac{d}{dt}{\displaystyle \underset{R}{\int }y\times \rho vdV}+{\displaystyle \underset{B}{\int }(y\times \rho v)v\cdot ndA}$

Mechanical Power Balance ${\displaystyle \underset{B}{\int }(n\cdot \sigma )\cdot vdA}+{\displaystyle \underset{R}{\int }\rho b\cdot v}dV={\displaystyle \underset{R}{\int }\sigma :D}dV+\frac{d}{dt}{\displaystyle \underset{R}{\int }\frac{1}{2}\rho (v\cdot v)dV}+{\displaystyle \underset{B}{\int }\frac{1}{2}\rho (v\cdot v)v\cdot ndA}$

First law of thermodynamics

${\displaystyle \underset{B}{\int }(n\cdot \sigma )\cdot v}dA+{\displaystyle \underset{R}{\int }\rho b\cdot v}dV-{\displaystyle \underset{B}{\int }q\cdot ndA}+{\displaystyle \underset{V}{\int }qdV}=\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho \left(\epsilon +\frac{1}{2}v\cdot v\right)dV}+{\displaystyle \underset{B}{\int }\rho \left(\epsilon +\frac{1}{2}v\cdot v\right)v\cdot n}dA$

Second law of thermodynamics

$\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho sdV}+{\displaystyle \underset{B}{\int }\rho s(v\cdot n)dA}+{\displaystyle \underset{B}{\int }\frac{q\cdot n}{\theta }dA}-{\displaystyle \underset{R}{\int }\frac{q}{\theta }dV}\ge 0$

 

 

These results can all be derived from the conservation laws for a material volume, using a similar approach.  Consider the mass conservation equation as a special case.   Start with the local form

${\frac{\partial \rho }{\partial t}|}_{y=const}+\frac{\partial \rho v_i}{\partial y_i}=0$

Integrate over a fixed spatial volume

${\displaystyle \underset{R}{\int }{\frac{\partial \rho }{\partial t}|}_{y=const}dV}+{\displaystyle \underset{R}{\int }\frac{\partial \rho v_i}{\partial y_i}dV}=0$

Note the R is independent of time, and use the divergence theorem

$\frac{d}{dt}{\displaystyle \underset{R}{\int }\rho (y,t)dV}+{\displaystyle \underset{B}{\int }\rho v_i{n}_{i}dA}=0$

As a second example, for the linear momentum balance equation, start with the local form

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\rho \left(\frac{\partial v_i}{\partial y_k}{v}_k+{\frac{\partial v_i}{\partial t}|}_{y_i=const}\right)$

Note that, using mass conservation

$\begin{array}{l}\frac{\partial }{\partial y_k}(\rho v_i{v}_k)=\rho v_k\frac{\partial v_i}{\partial y_k}+\frac{\partial (\rho v_k)}{\partial y_k}{v}_i=\rho v_k\frac{\partial v_i}{\partial y_k}-\frac{\partial \rho }{\partial t}{v}_i\\ \Rightarrow \rho v_k\frac{\partial v_i}{\partial y_k}=\frac{\partial }{\partial y_k}(\rho v_i{v}_k)+\frac{\partial \rho }{\partial t}{v}_i\end{array}$

Therefore

$\frac{\partial {\sigma }_{ji}}{\partial y_j}+\rho b_i=\frac{\partial }{\partial y_k}(\rho v_i{v}_k)+{v_i\frac{\partial \rho }{\partial t}|}_{y_i=const}+\rho {\frac{\partial v_i}{\partial t}|}_{y_i=const}=\frac{\partial }{\partial y_k}(\rho v_i{v}_k)+{\frac{\partial (\rho v_i)}{\partial t}|}_{y_i=const}$

Integrating this expression over the fixed control volume and using the divergence theorem gives the stated answer.

 

A similar approach can be used to obtain the remaining results $–$ details are left as an exercise.

 

 

 

5.12 Transformation of kinematic and kinetic variables under changes of reference frame

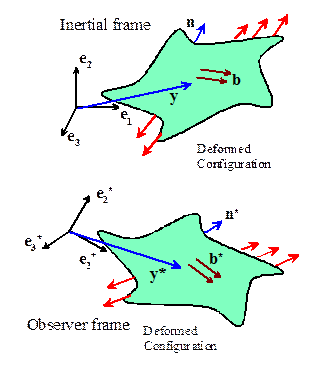
Since physical laws must be constructed so as to be independent of the choice of reference frame, the behavior of kinematic and kinetic variables, the field equations, and constitutive equations under a change of reference frame is of interest.  The concept of a reference frame, and the various relations involved in changing reference frames, are both rather obscure concepts.   There are several reasons for this:

1.      One source of confusion arises because Newtonian mechanics relies on the concept of an inertial frame, and Newton’s law F=ma only holds in this frame.   The statement ‘the laws of physics are independent of reference frame’ does not mean that F=ma in all reference frames $–$ it means that all observers must describe Newton’s laws with respect to the same inertial frame, and must do so in a consistent manner.  Frame indifference is not the theory of relativity…

2.      A second source of confusion stems from the use of a reference configuration to quantify shape changes of a solid.   We nearly always use the undeformed solid as reference, which gives the impression that the reference configuration, like the deformed configuration, is associated with the inertial frame.   In fact, the reference configuration is completely arbitrary, and even though all observers might choose the same initial configuration of a solid as reference, they will all assume that the reference configuration is fixed.   The reference configuration is not attached to the inertial frame.  Moreover, since the reference configuration is arbitrary, two observers could choose different reference configurations, and still devise equations that describe the same physical process.  Of course the exact form of the governing equations will change with the choice of reference configuration.  There are no restrictions governing transformation of reference configuration between observers, beyond the fact that two reference configurations must be related by an invertible 1:1 mapping.

 

To make the concept of a change in reference frame in classical continuum mechanics precise, we first introduce the intertial frame.  As in all preceding discussions, we assume that the inertial frame is a three-dimensional Euclidean space, and let $y(t)$ denote a point in the inertial frame.  We then define Newtonian measures of velocity and acceleration vectors in the usual way as

$v=\frac{\partial y}{\partial t}a=\frac{{\partial }^{2}y}{\partial t^2}$

 

This inertial frame could be viewed by an observer who rotates and translates with respect to the inertial frame.  To this observer, all physical quantities associated with the inertial frame would appear to be translated and rotated in the opposite sense.  We describe this apparent transformation of space with respect to the observer as a rigid rotation and translation $–$ thus, the position vector of a point seen by the observer is related to position in the inertial frame by

$y^{*}=y_0^{*}(t)+Q(t)(y-y_0)$

where $y_0$ is an arbitrary fixed point in the inertial frame, $y_0^{*}$ is an arbitrary vector, and  $Q(t)$ is a proper orthogonal tensor, representing a rigid rotation.  It is convenient to introduce the spin associated with the relative rotation of the inertial frame and the observer’s frame

$\Omega =\frac{dQ}{dt}{Q}^T$

 

We will denote quantities in the observer’s reference frame with a star superscript; -for example mass density, body force, Cauchy stress ${\rho }^{*},b^{*},{\sigma }^{*}$ ; those without superscripts will be assumed to be defined in the inertial frame.

 

All observable physical quantities must transform in particular ways under a change of observer.  Specifically:

 Scalar quantities, such as density or temperature are invariant $–$ they have the same value in all reference frames.

 Quantities such as body force, a line element in the deformed solid; the normal to a surface; the velocity vector, the acceleration vector, and so on, are physical vectors defined in the inertial reference frame.   They can be regarded as connecting two points in the inertial frame, and must transform with the line connecting these two points under a change of reference frame.  Thus, a normal vector to a deformed surface, body force, velocity, acceleration vectors must transform as

$b^{*}=Qb{n}^{*}=Qn{v}^{*}=Qv{a}^{*}=Qa$

Vectors that transform in this way are said to be frame indifferent, or objective.   Note (1) frame indifference does not mean that vectors are invariant $–$ quite the opposite, in fact $–$ it means that all observers must describe the same physical quantity; (2) vector quantities we make frequent use of in solid mechanics need not necessarily be frame indifferent.   For example, the normal to the reference configuration of a solid would not be frame indifferent; nor would a material fiber within the reference configuration.

 Tensor quantities that map a frame indifferent vector onto another frame independent vector are similarly said to be frame indifferent, or objective. Examples include the stretch rate tensor (which specifies the relative velocity of two ends of an infinitesimal material fiber in the spatial configuration); or Cauchy stress (which maps the normal to a surface in the spatial configuration to the physical traction vector.  A frame indifferent tensor must transform as

${\sigma }^{*}=Q\sigma Q^T{D}^{*}=QD{Q}^T$

Again, not all tensors are frame indifferent.  The deformation gradient; the spin tensor; the Lagrange strain tensor are not frame indifferent.

 

Frame indifference can also be looked at as follows.   Let $\{e_1,e_2,e_3\}$ be an inertial basis.   Under a change of observer, the basis vectors transform as $\{e_1^{*},e_2^{*},e_3^{*}\}=\{Q{e}_1,Q{e}_2,Q{e}_3\}$ (relative to the observer, they appear to rotate with the observed frame.  It is important to note that $\{e_1^{*},e_2^{*},e_3^{*}\}$ are time dependent).    Now, we can compute components in either basis

$\begin{array}{l}{b}_i^{*}=e_i^{*}\cdot b^{*}=Q{e}_i\cdot Qb=e_i\cdot Q^{T}Qb=e_i\cdot b=b_i\\ {\sigma }_{ij}^{*}=e_i^{*}\cdot {\sigma }^{*}\cdot e_j^{*}=Q{e}_i\cdot Q\sigma Q^{T}Q{e}_j={\sigma }_{ij}\end{array}$

The components of a vector with respect to a basis that rotates with an inertial frame is independent of the observer.  This is one interpretation of what we mean by a physical process being independent of the observer.

 

We now examine how several kinematic and kinetic variables commonly used in continuum mechanics transform under a change of observer.   To describe deformations, a reference configuration must be selected.  A material particle in the reference configuration is identified by a time independent vector X in reference space.   The choice of reference space is arbitrary; and there is no reason why different observers will necessarily adopt the same reference space.   Discussions are greatly simplified, however, if we choose to assume that all observers use the same space for the reference configuration (behavior under a change of reference configuration can be treated separately).

 

        

 The deformation mapping transforms as $y^{*}(X,t)=y_0^{*}(t)+Q(t)\left(y(X,t)-y_0\right)$

 The deformation gradient transforms as $F^{*}=\frac{\partial y^{*}}{\partial X}=Q\frac{\partial y}{\partial X}=QF$

 The right Cauchy Green strain  Lagrange strain, the right stretch tensor are invariant

$C^{*}=F^{*T}{F}^{*}=F^T{Q}^{T}QF=C{E}^{*}=E{U}^{*}=U$

 The left Cauchy Green strain, Eulerian strain, left stretch tensor are frame indifferent

$B^{*}=F^{*}{F}^{*T}=QF{F}^T{Q}^T=QC{Q}^T{V}^{*}=QV{Q}^T$

 The velocity gradient and spin tensor transform as

$\begin{array}{l}{L}^{*}={\dot{F}}^{*}{F}^{*-1}=\left(\dot{Q}F+Q\dot{F}\right)F^{-1}{Q}^T=QL{Q}^T+\Omega \\ W^{*}=(L^{*}-L^{*T})/2=QW{Q}^T+\Omega \end{array}$

 The velocity and acceleration vectors transform as

$\begin{array}{l}{v}^{*}=Qv=Q\frac{dy}{dt}=Q\frac{d}{dt}{Q}^T(y^{*}-y_0^{*}(t))=\frac{d{y}^{*}}{dt}-\frac{d{y}_0^{*}}{dt}-\Omega (y^{*}-y_0^{*}(t))\\ a^{*}=Qa=Q\frac{d^{2}y}{d{t}^2}=Q\frac{d^2}{d{t}^2}{Q}^T(y^{*}-y_0^{*}(t))=\frac{d^2{y}^{*}}{d{t}^2}-\frac{d^2{y}_0^{*}}{d{t}^2}+\left({\Omega }^2-\frac{d\Omega }{dt}\right)(y^{*}-y_0^{*}(t))-2\Omega (\frac{d{y}^{*}}{dt}-\frac{d{y}_0^{*}(t)}{dt})\end{array}$

(the additional terms in the acceleration can be interpreted as the centripetal and coriolis accelerations)

 The Cauchy stress is frame indifferent ${\sigma }^{*}=Q\sigma Q^T$ (you can see this from the formal definition, or use the fact that the virtual power must be invariant under a frame change)

 The material stress is frame invariant ${\Sigma }^{*}=\Sigma$

 The nominal stress transforms as $S^{*}=J{(QF)}^{-1}\cdot Q\sigma Q^T=J{F}^{-1}\cdot \sigma Q^T=S{Q}^T$ (note that this transformation rule will differ if the nominal stress is defined as the transpose of the measure used here…)

 

By this time you are probably asking yourself why anyone could possibly care about all this.   This is a fair question $–$ issues of frame indifference arise rather rarely in practice. They do come up, however, when we define constitutive equations for a material $–$ which must relate deformation measures to internal force measures.  A new constitutive equation is a new physical law $–$ and it is important to make sure that the new law behaves correctly under a change of observer.  Most modern constitutive equations try to describe the underlying microscopic processes that govern its response, and if this is done properly, the law will be frame indifferent.   But some constitutive laws are just curve-fits $–$ some mathematical relationship between a deformation measure and a force measure $–$ and not all possible relationships will transform correctly.  

 

Problems arise most commonly in trying to develop rate forms of constitutive equations, which are intended to relate some measure of strain rate to stress rate.   This is because, even if a vector or tensor is itself frame indifferent, its time derivative is generally not.  For example, although position vector satisfies $y^{*}=Qy$ and is frame indifferent, this does not mean that $\frac{d{y}^{*}}{dt}=Q\frac{dy}{dt}$.  Similarly, for the rate of change of Cauchy stress is not frame indifferent, because

$\frac{d{\sigma }^{*}}{dt}=\frac{dQ}{dt}\sigma Q^T+Q\frac{d\sigma }{dt}{Q}^T+Q\sigma {\frac{dQ}{dt}}^T=Q\frac{d\sigma }{dt}{Q}^T+\Omega {\sigma }^{*}-{\sigma }^{*}\Omega \ne Q\frac{d\sigma }{dt}{Q}^T$

In fact, only quantities that are invariant under a change of observer can be differentiated safely with respect to time $–$ their time derivatives remain invariant.

 

This means that if constitutive equations are expressed in rate form $–$ for example something that looks at first glance like the rate form of an elastic constitutive equation

$\frac{d\sigma }{dt}=\tilde{C}D$

(here C is a fourth order constant tensor) $–$ the constitutive equation will not be frame indifferent.  

 

There are various fixes for this $–$ the constitutive law can be written in terms of invariant quantities (eg by relating the rate of change of material stress to Lagrange strain rate); they can be derived from physical principles, in which case frame indifferent measures usually emerge naturally from the treatment; or frame indifferent measures of time derivatives can be specially constructed.

 

As a specific example, one way to construct a frame indifferent stress rate is to use the rate of change of stress components with respect to a basis that rotates with the solid (this is what an observer rotating with the material would actually see).  This sounds easy $–$ we just choose some basis vectors $\{m_1,m_2,m_3\}$ with each basis vector parallel to a particular material fiber.  But this doesn’t quite work, because of course the basis vectors won’t generally remain orthogonal under an arbitrary deformation.   So rather than attach $\{m_1,m_2,m_3\}$ to particular material fibers, we simply suppose that they rotate with the average angular velocity of all material fibers passing through a particular point.  This means that

$\frac{d{m}_i}{dt}=W{m}_i$

where W is the spin tensor.  Now, the time derivative of stress can be written as

$\frac{d\sigma }{dt}=\frac{d}{dt}({\sigma }_{ij}{m}_i\otimes m_j)=\frac{d{\sigma }_{ij}}{dt}{m}_i\otimes m_j+{\sigma }_{ij}W{m}_i\otimes m_j+{\sigma }_{ij}{m}_i\otimes W{m}_j=\stackrel{\nabla }{\sigma }+W\sigma -\sigma W$

Here, the first term can be interpreted as the stress rate seen by an observer rotating with the embedded basis; the second and third are the rates of change of stress arising from the rotation of the material.  The first term is of particular interest, and is called the Jaumann stress rate.  It is defined as

$\stackrel{\nabla }{\sigma }=\frac{d\sigma }{dt}-W\sigma +\sigma W$

It is easy to show that $\stackrel{\nabla }{\sigma }$ is frame indifferent.  Many constitutive equations assume that material stretch rate is proportional to this special stress rate.  For example, we could write

$\stackrel{\nabla }{\sigma }=\tilde{C}D$

Provided that $\tilde{C}$ is a frame indifferent fourth-order tensor, this constitutive equation would be frame indifferent.

 

This raises another question, of course.   What does it mean for a fourth-order tensor to be frame indifferent?   Hopefully you can answer this question for yourself!