8. Mechanics of Elastic Solids
In this chapter, we apply the general equations of continuum mechanics to elastic solids.
As
a philosophical preamble, it is interesting to contrast the challenges
associated with modeling solids to the fluid mechanics problems discussed in
the preceding chapter. In fluid mechanics, there tends to be little debate
about the choice of a model to describe the behavior of the fluid itself often, relatively simple idealizations, such
as the Eulerian fluid, or Newtonian Viscous behavior, are sufficient. This is because a lot of fluid mechanics is
concerned with high Reynolds number flows, in which case inertia forces are
much more important than the forces generated by the deformation.
Inertia nearly always plays a secondary role in solid mechanics problems (again, there are exceptions, such as in modeling a car crash or explosion, but the majority of solid mechanics is concerned with quasi-static equilibrium). The internal forces generated by the deformation itself dominate the response. Characterizing the stress-strain relation of the material thus becomes a paramount concern. As a result, there are huge numbers of different material models for solids. These models must be chosen and calibrated carefully in any application.
There are three general classes of material model for solids
1.
Elasticity (with
or without heating effects). Material
behavior in these models is perfectly reversible any irreversibility comes from heat flow
effects, which are often neglected.
2.
Viscoelasticity these materials display irreversible and
possibly time-dependent behavior, but the irreversible response is modeled
using fairly simple linear relations between stress and rate of deformation
3.
Plasticity plasticity models account for irreversible
behavior using sophisticated nonlinear relations.
We
will not be able to discuss all these material models in detail in this course there are entire courses devoted to the theory
of elasticity, viscoelasticity and plasticity, which you are no doubt looking
forward to taking. Instead, we will
focus on the two simplest ones: elastic, and viscoelastic material behavior. The discussion serves two purposes. Firstly, to illustrate how constitutive
relations for solids are constructed; and secondly, to provide a short
introduction to some of the methods that are used to solve solid mechanics
problems.
8.1 Overview of elastic material models
There are two general types of elastic material.
Linear elastic constitutive relations model reversible behavior of a material that is subjected to small strains. Nearly all solid materials can be represented by linear elastic constitutive equations if they are subjected to sufficiently small stresses. Since the strains are small, all the governing equations for linear elastic materials can be linearized, and are therefore relatively easy to solve. Linear elasticity theory is thus the best known and most widely used branch of solid mechanics.
Hyperelastic constitutive laws are used to model materials that
respond elastically when subjected to very large strains. They account both for
nonlinear material behavior and large shape changes. The main applications of the theory are (i)
to model the rubbery behavior of a polymeric material, and (ii) to model
polymeric foams that can be subjected to large reversible shape changes (e.g. a
sponge).
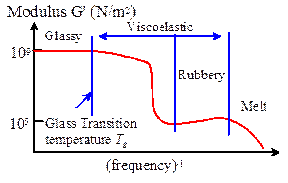
In general, the response of a typical polymer is strongly dependent on temperature, strain history and loading rate. The behavior will be described in more detail in the next section, where we present the theory of viscoelasticity. For now, we note that polymers have various regimes of mechanical behavior, referred to as `glassy,’ `viscoelastic’ and `rubbery.’ The various regimes can be identified for a particular polymer by applying a sinusoidal variation of shear stress to the solid and measuring the resulting shear strain amplitude. A typical result is illustrated in the figure, which shows the apparent shear modulus (ratio of stress amplitude to strain amplitude) as a function of temperature.
At a critical temperature known as the glass transition temperature,
a polymeric material undergoes a dramatic change in mechanical response. Below this temperature, it behaves like a
glass, with a stiff response. Near the glass transition temperature, the stress
depends strongly on the strain rate. At
the glass transition temperature, there is a dramatic drop in modulus. Above this temperature, there is a regime
where the polymer shows `rubbery’ behavior the response is elastic; the stress does not
depend strongly on strain rate or strain history, and the modulus increases
with temperature. All polymers show
these general trends, but the extent of each regime, and the detailed behavior
within each regime, depend on the solid’s molecular structure. Heavily cross-linked polymers (elastomers)
are the most likely to show ideal rubbery behavior. Hyperelastic constitutive laws are intended
to approximate this `rubbery’ behavior.
Features of the behavior of a solid rubber:
1. The material is close to ideally elastic. i.e. (i) when deformed at constant temperature or adiabatically, stress is a function only of current strain and independent of history or rate of loading, (ii) the behavior is reversible: no net work is done on the solid when subjected to a closed cycle of strain under adiabatic or isothermal conditions.
2. The material strongly resists volume changes. The bulk modulus (the ratio of volume change to hydrostatic component of stress) is comparable to that of metals or covalently bonded solids;
3. The material is very compliant in shear shear modulus is of the order of
times that of most metals;
4. The material is isotropic its stress-strain response is independent of
material orientation.
5. 
The shear modulus is temperature dependent: the
material becomes stiffer as it is heated, in sharp contrast to metals;
6. When stretched, the material gives off heat.
Polymeric foams (e.g. a sponge) share some of these properties:
1. They are close to reversible, and show little rate or history dependence.
2. In contrast to rubbers, most foams are highly
compressible bulk and shear moduli are comparable.
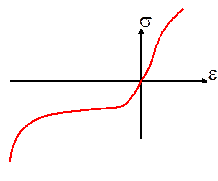
3. Foams have a complicated true stress-true strain response, generally resembling the figure to the right. The finite strain response of the foam in compression is quite different to that in tension, because of buckling in the cell walls.
4. Foams can be anisotropic, depending on their cell structure. Foams with a random cell structure are isotropic.
In the following, we will discuss both types of constitutive relation. Perhaps perversely, we start with the more complex, hyperelastic model first. The governing equations for the nonlinear case can then be linearized to obtain the simpler theory of linear elasticity.
8.2 Summary of governing equations for elastic solids
Unlike
fluids, solids nearly always have a well- defined reference configuration
(there are a few exceptions for example a solid could change its shape by
diffusion, or a biological material could grow). When solving a solid mechanics problem, we
therefore have the option to write the governing equations in terms of
deformation and force measures associated with the reference configuration, if
this is convenient.
The
central problem in a solid mechanics problem is generally to determine the displacement
field ,
Cauchy stress distribution
(or some other stress measure) and (sometimes)
temperature
,
as functions of position (usually as function of position in the reference
configuration) and time. The solid is
characterized by the following physical quantities:
The mass density per unit reference volume
The specific internal energy
The specific entropy
The specific Helmholtz free energy
A stress response function, e.g. . Here,
is the material stress
one can use response functions for other
stress measures as well.
A heat flux response function . In actual calculations for solids it is often
preferable to define a heat fluxe response function that characterizes heat
flow through the reference configuration
an appropriate measure is defined below.
Body forces: The solid is subjected to an external body force per unit mass.
Its motion is characterized by the usual deformation measures
Deformation Gradient
The polar decomposition
The
Right and Left Cauchy-Green Tensors
Lagrange Strain Tensor
Invariants of the various strain tensors. For example, invariants of B are frequently used in constitutive
models for isotropic hyperelastic materials
An alternative set of invariants of B (more convenient for models of nearly
incompressible materials note that
remain constant under a pure volume change)
Principal stretches and principal stretch
directions
1. Let denote the three eigenvalues of B. The principal stretches are
2. Let denote three, mutually perpendicular unit eigenvectors of B. These define the principal stretch
directions. (Note: since B is symmetric its eigenvectors are
automatically mutually perpendicular as long as no two eigenvalues are the
same. If two, or all three eigenvalues
are the same, the eignevectors are not uniquely defined
in this case any convenient mutually
perpendicular set of eigenvectors can be used).
3. Recall that B
can be expressed in terms of its eigenvectors and eigenvalues as
Heat Flow Measures: In fluid mechanics, we always characterize heat flux by the flow of heat through the deformed solid. In solid mechanics, it is convenient to introduce another measure, defined as
This new heat flux vector can be interpreted physically as the heat flux crossing an area element in the undeformed solid, in the sense that
is
the heat flux crossing an area element with area and normal m in the reference configuration.
Stress Measures: Usually stress-strain laws are given as equations
relating Cauchy stress (`true’ stress) to left Cauchy-Green deformation tensor. For some computations it may be more
convenient to use other stress measures.
They are defined below, for convenience.
The Cauchy (“true”) stress represents the
force per unit deformed area in the solid and is defined by
Kirchhoff stress
Nominal (First Piola-Kirchhoff) stress
Material
(Second Piola-Kirchhoff) stress
Conservation Laws (expressed on the reference configuration)
Mass
Conservation (satisfied trivially)
Linear momentum conservation
Energy conservation
(you
should be able to verify for yourself that and
are work conjugate)
Finally the constitutive law must satisfy the Entropy Inequality:
Transformations under observer changes:
Deformation Gradient
Left C-G tensor, left stretch
Cauchy Stress
Nominal Stress
Material
Stress
8.3 General form for constitutive equations for elastic solids:
We now list the most general form of the constitutive equations for elastic solids that are consistent with frame indifference and the entropy inequality. In practice, most problems of interest are approximated using one of several special cases of the general equations. These will be listed separately.
To be consistent with frame indifference and the laws of thermodynamics, the specific free energy, internal energy, Helmholtz free energy, stress response function and heat transfer function must have the forms
Specific internal energy
Specific entropy
Specific Helmholtz free energy
Stress response function
Heat flux response function
It
is useful also to introduce the specific
heat
Then, the stress response function, free energy, entropy and specific heat capacity are related by
In addition, the heat flux function must satisfy
We next summarize the reasoning that leads to these conclusions:
·
We assume at the
outset that the state of the material (and all the constitutive response
functions) depend only on the current shape and temperature of the solid, and
are independent of load history and the rate of deformation. In addition, we assume that the constitutive
behavior is local in other words the constitutive response at a
material point depends only on the shape and temperature of a vanishingly small
element of material surrounding that point.
This means that the constitutive functions can only depend on the
deformation gradient F and
temperature
.
· Frame indifference shows that the free energy function and the stress and heat transfer response functions depend only on C. To see this, note that frame indifference requires that
for all proper orthogonal tensors . Recall that
. If we choose
then
applying frame indifference shows that the
stress response functions must have the form
i.e it must always be possible to express the constitutive functions so that they are functions of C only (and are thus independent of the rotation in the polar decomposition of F).
· The free energy inequality provides the remaining conclusions. Take the time derivative of the free energy function and substitute into the free energy inequality to see that
(time derivatives are all with fixed x). Collecting coefficients of rate quantities gives
This
inequality must hold for all possible ,
which can all be independently prescribed.
It follows immediately that
· The first two relations here immediately show that
The definitions of free energy and heat capacity also show that
Natural Reference Configuration
The preceding equations hold for any choice of reference configuration. In many applications it is convenient to select the reference configuration so that it is stress free at some reference temperature. This means that the stress response function and Helmholtz free energy satisfy
8.4 Restrictions imposed by material symmetry
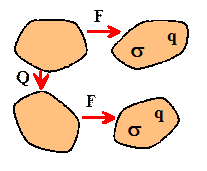
A symmetry transformation is defined as a proper orthogonal transformation of the reference configuration that leaves the material response unchanged. For example, for the free energy
This
looks rather similar to the objectivity constraint but the sequence is important
note that F
and Q are reversed in this
definition.
You can visualize this definition as an experiment in which (i) a material is subjected to some deformation gradient F and temperature gradient, and the response functions are determined (eg by measuring the stress and heat flux in the deformed solid); and (ii) The specimen is first rotated by a rigid rotation Q and is then subjected to the same deformation F and temperature gradient, and the stress and heat flux are measured again. If the stress is the same in both experiments, Q is a symmetry transformation.
Note that we require the free energy, heat flux and Cauchy stress in the deformed solid to be the same when the material is subjected to FQ and F. Since the reference configuration has changed, the material stress and the material heat flux vector are not invariant to a symmetry transformation.
Isotropic solids are of particular interest. These are materials that are unchanged by all proper orthogonal transformations of the reference configuration. For isotropic solids, the constitutive response can be expressed in terms of the left Cauchy Green tensor. To see this, note that isotropy requires that
for
all proper orthogonal tensors Q.
If we let F=VR and choose Q=R, then ,
which implies that
Isotropic materials therefore have a free energy that depends only on B. The nature of the free energy function is restricted further by objectivity, which requires that
for
all proper orthogonal tensors Q. This means that can only be a function of the invariants of B.
The functions themselves must be determined experimentally. Some specific functions that are frequently used are listed in Section 7.5.
8.5 Calculating stress-strain relations from the free energy
The constitutive law for a hyperelastic material is defined by an
equation relating the free energy of the material to the deformation gradient,
or, for an isotropic solid, to the three invariants of the strain tensor. In practice, rather than specifying the
specific free energy, most constitutive laws specify the strain energy density (per unit reference volume) rather than the
free energy, just to avoid introducing the mass density in the stress-strain
relations. The strain energy is related
to the Helmholtz free energy by ,
and can be expressed in one of several forms
The stress-strain law must then be deduced by differentiating the free energy. This can involve some tedious algebra. Formulas are listed below for the stress-strain relations for each choice of strain invariant. The expressions give Cauchy stress which is what we are usually trying to calculate. The results are derived below
Strain
energy density in terms of
Strain
energy density in terms of
Strain
energy density in terms of
Strain
energy density in terms of
Derivations: We start by
deriving the general formula for stress in terms of :
- The free energy inequality can be expressed in terms of F and the nominal stress S as
2. Therefore,
This
must hold for all possible ,so
that
3. Finally, the formula for Cauchy stress follows from
the equation relating to
For an isotropic material, it is necessary to find derivatives of the invariants with respect to the components of F in order to compute the stress-strain function for a given strain energy density. It is straightforward, but somewhat tedious to show that:
Then,
and
When using a strain energy density of the form , we will have to compute the derivatives of
the invariants
with respect to the components of F in order to find
We find that
Thus,
Next, we derive the stress-strain relation in terms of
a strain energy density that is expressed as a function of the
principal strains. Note first that
so that the chain rule gives
Using this and the expression that relates the stress components to the derivatives of U,
we find that the
principal stresses are related to the corresponding principal
stretches
(square-roots of the eigenvalues of B) through
The spectral
decomposition for B in terms of its
eigenvalues and eigenvectors
:
now allows the stress tensor to be written as
8.6 Perfectly incompressible materials
The preceding formulas assume that the material has
some (perhaps small) compressibility that is to say, if you load it with
hydrostatic pressure, its volume will change by a measurable amount. Most rubbers strongly resist volume changes,
and in hand calculations it is sometimes convenient to approximate them as
perfectly incompressible. The material
model for incompressible materials is specified as follows:
The deformation must satisfy J=1 to preserve volume.
The strain energy density is therefore only a
function of two invariants;
furthermore, both sets of invariants defined above are identical. We can use a strain energy density of the
form .
Because you can apply any pressure to an
incompressible solid without changing its shape, the stress cannot be uniquely
determined from the strains. Consequently,
the stress-strain law only specifies the deviatoric
stress . In problems involving quasi-static loading,
the hydrostatic stress
can usually be calculated, by solving the
equilibrium equations (together with appropriate boundary conditions). Incompressible materials should not be used
in a dynamic analysis, because the speed of elastic pressure waves is infinite.
The formula for stress in terms of has the form
The hydrostatic stress p is an unknown variable, which must be calculated by solving the boundary value problem.
8.7 Specific forms of the strain energy density
Generalized
Neo-Hookean solid (Adapted from Treloar, Proc Phys Soc 60
135-44 1948)
where and
are material properties (for small
deformations,
and
are the shear modulus and bulk modulus of the
solid, respectively). Elementary statistical mechanics treatments predict that
,
where N is the number of polymer chains per unit volume, k is the
Boltzmann constant, and T is
temperature. This is a rubber elasticity
model, for rubbers with very limited compressibility, and should be used with
. The stress-strain relation follows as
The fully incompressible limit can be obtained by
setting in the stress-strain law.
Generalized
Mooney-Rivlin solid (Adapted
from Mooney, J Appl Phys 11 582 1940)
where and
are material properties. For small deformations, the shear modulus and
bulk modulus of the solid are
and
. This is a rubber elasticity model, and should
be used with
.
The stress-strain relation follows as
Generalized
polynomial rubber elasticity potential
where and
are material properties. For small strains the shear modulus and bulk
modulus follow as
.
This model is implemented in many finite element codes. Both the neo-Hookean solid and the
Mooney-Rivlin solid are special cases of the law (with N=1 and appropriate choices of
).
Values of
are rarely used, because it is difficult to
fit such a large number of material properties to experimental data.
where , and
are material properties. For small strains the shear modulus and bulk
modulus follow as
.
This is a rubber elasticity model, and is intended to be used with
. The stress can be computed using the formulas
in the preceding section, but are too lengthy to write out in full here.
Arruda-Boyce 8 chain model (J. Mech. Phys. Solids, 41, (2)
389-412, 1992)
where are material properties. For small deformations
are the shear and bulk modulus, respectively.
This is a rubber elasticity model, so
. The potential was derived by calculating the
entropy of a simple network of long-chain molecules, and the series is the
result of a
Ogden-Storakers hyperelastic foam
where are material properties. For small strains the shear modulus and bulk
modulus follow as
. This is a foam model, and can model highly
compressible materials. The shear and
compression responses are coupled.
Blatz-Ko foam rubber
where is a material parameter corresponding to the
shear modulus at infinitesimal strains. Poisson’s ratio for such a material is
0.25.
8.8 Calibrating nonlinear elasticity models
To use any of these constitutive relations, you will
need to determine values for the material constants. In some cases this is quite simple (the incompressible
neo-Hookean material only has 1 constant!); for models like the generalized
polynomial or
Conceptually, however, the procedure is straightforward. You can perform various types of test on a sample of the material, including simple tension, pure shear, equibiaxial tension, or volumetric compression. It is straightforward to calculate the predicted stress-strain behavior for the specimen for each constitutive law. The parameters can then be chosen to give the best fit to experimental behavior.
Here are some guidelines on how best to do this:
1. When modeling the behavior of rubber under ambient
pressure, you can usually assume that the material is nearly incompressible,
and don’t need to characterize response to volumetric compression in
detail. For the rubber elasticity models
listed above, you can take MPa. To fit the remaining parameters, you can
assume the material is perfectly incompressible.
2. If rubber is subjected to large hydrostatic stress (>100 MPa) its volumetric and shear responses are strongly coupled. Compression increases the shear modulus, and high enough pressure can even induce a glass transition (see, e.g. D.L. Quested, K.D. Pae, J.L. Sheinbein and B.A. Newman, J. Appl. Phys, 52, (10) 5977 (1981)). To account for this, you would have to use one of the foam models: in the rubber models the volumetric and shear responses are decoupled. You would also have to determine the material constants by testing the material under combined hydrostatic and shear loading.
3. 
For the simpler material models, (e.g. the neo-Hookean
solid, the Mooney-Rivlin material, or the Arruda-Boyce model, which contain
only two material parameters in addition to the bulk modulus) you can estimate
material parameters by fitting to the results of a uniaxial tension test. There are various ways to actually do the fit
you could match the small-strain shear modulus
to experiment, and then select the remaining parameter to fit the stress-strain
curve at a larger stretch. Least-squared
fits are also often used. However,
models calibrated in this way do not always predict material behavior under
multiaxial loading accurately.
4. A more accurate description of material response to
multiaxial loading can be obtained by fitting the material parameters to
multiaxial tests. To help in this
exercise, the nominal stress (i.e.
force/unit undeformed area) v-
extension predicted by several constitutive laws are listed in the table below
(assuming perfectly incompressible behavior, as suggested in 1.)
|
|
Uniaxial Tension |
Biaxial Tension |
Pure Shear |
|
Invariants |
|
|
|
|
Neo-Hookean |
|
|
|
|
Mooney-Rivlin |
|
|
|
|
Arruda-Boyce |
|
|
|
|
|
|||
|
|
|
|
|
8.9 Representative values of material properties for rubbers
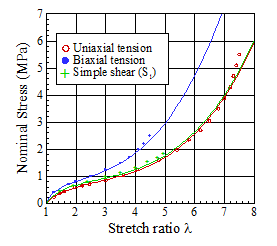
The properties of rubber are strongly sensitive to its molecular
structure, and for accurate predictions you will need to obtain experimental
data for the particular material you plan to use. As a rough guide, the experimental data of
Treloar (Trans. Faraday Soc. 40, 59.1944) for the behavior of
vulcanized rubber under uniaxial tension, biaxial tension, and pure shear is
shown in the picture. The solid lines in
the figure show the predictions of the
Material parameters fit to this data for several constitutive laws are listed below.
|
Neo-Hookean |
|
|
Mooney-Rivlin |
|
|
Arruda-Boyce |
|
|
|
|
8.10 Example boundary value problems with large deformations
The equations governing large deformation of elastic solids are nonlinear and are impossible to solve analytically in general. Solutions are known for a few very simple geometries. More general can be found using numerical methods such as the finite element method (but rubber-like material models pose some special challenges for finite element analysis).
Spherically Symmetric Problems
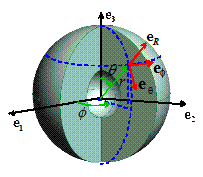
A representative spherically symmetric problem is illustrated
in the picture. We consider a hollow,
spherical solid, which is subjected to spherically symmetric loading (i.e.
internal body forces, as well as tractions or displacements applied to the
surface, are independent of and
,
and act in the radial direction only).
The solution is most conveniently expressed using a
spherical-polar coordinate system, illustrated in the figure. For a finite deformation problem, we need a
way to characterize the position of material particles in both the undeformed
and deformed solid. To do this, we let identify a material particle in the undeformed
solid. The coordinates of the same point in the deformed solid is identified by
a new set of spherical-polar co-ordinates
. One way to describe the deformation would be
to specify each of the deformed coordinates
in terms of the reference coordinates
.
For a spherically symmetric deformation, points only move radially, so that
In finite deformation problems vectors and tensors can be
expressed as components in a basis associated with the position of material
points in the undeformed solid, or, if more convenient, in a basis
associated with material points in the
deformed solid. For spherically
symmetric deformations the two bases are identical
consequently, we can write
Position vector in the undeformed solid
Position vector in the deformed solid
Displacement
vector
The
stress, deformation gradient and deformation tensors tensors (written as
components in ) have the form
and
furthermore must satisfy
.
For spherical symmetry, the governing equations reduce to
Strain Displacement Relations
Incompressibility condition
StressStrain
relations
Equilibrium Equations
Boundary Conditions
Prescribed Displacements
Prescribed Tractions
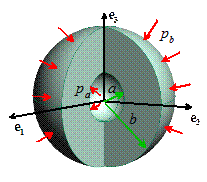As an example, consider a pressurized
hollow rubber shell, as shown in the picture. Assume that
Before deformation, the sphere has inner
radius A and outer radius B
After deformation, the sphere has inner radius
a and outer radius b
The solid is made from an incompressible
Mooney-Rivlin solid, with strain energy potential
No body forces act on the sphere
The inner surface r=a is subjected to pressure
The outer surface r=b is subjected to pressure
The deformed radii a,b of the inner and outer surfaces of the spherical shell are related to the pressure by
where ,
,
and
are related by
Provided the pressure is not too large (see below), the
preceding two equations can be solved for and
given the pressure and properties of the shell
(for graphing purposes, it is better to assume a value for
,
calculate the corresponding
,
and then determine the pressure).
The position r of a material particle after deformation is related to its position R before deformation by
The deformation tensor distribution in the sphere is
The Cauchy stress in the sphere is
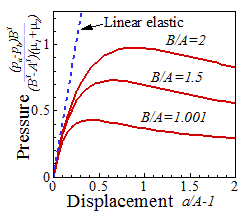The variation of the internal radius
of the spherical shell with applied pressure is plotted in the figure, for (a representative value for a typical
rubber). For comparison, the linear
elastic solution (obtained by setting
and
in the formulas given in section 4.1.4) is
also shown. Note that:
1. The small strain solution is accurate
for
2. The relationship between pressure and displacement is nonlinear in the large deformation regime.
3. As the internal radius of the sphere increases, the pressure reaches a maximum, and thereafter decreases (this will be familiar behavior to anyone who has inflated a balloon). This is because the wall thickness of the shell decreases as the sphere expands.
The stress distribution for various displacements in the
shell is plotted in the figures below, for ,
and B/A=3. The radial stress remains
close to the linear elastic solution even in the large deformation regime. The hoop stress distribution is significantly
altered as the deformation increases, however.
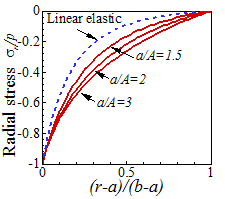
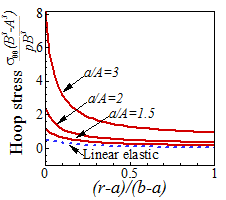
Derivation
1. Integrate the incompressibility condition from the inner radius of the sphere to some arbitrary point R
2. Note that by definition, and
since the point at R=A moves to r=a after
deformation. This gives the relationship
between the position r of a point in
the deformed solid and its position R
before deformation
3.
The components of
the Cauchy-Green tensor follow as
4. The stresses follow from the stress-strain equation as
5.
Substituting
these stresses into the equilibrium equation leads to the following
differential equation for
6.
After
substituting for and
,
and expressing R in terms of r, this equation can be integrated and
simplified to see that
7.
The
boundary conditions require that on (r=a,R=A),
while
on (r=b,R=B),
which requires
where and
. The expression that relates
and
to the pressure follows by subtracting the
first equation from the second. Adding
the two equations gives the expression for C.
8. Finally, the hoop stress follows by
noting that, from (4)
8.11 Linearized field equations for elastic materials
In the majority of practical applications, the displacement of the solid is small, in which case the governing equations can be linearized. For this purpose, we assume
1. The solid has a stress free reference configuration at
some reference temperature (this is not essential it is possible to work with a stressed
reference configurations).
2. The displacement gradients are small.
We then approximate the field equations as follows:
The mass density is equal in both reference
and deformed configurations
The Lagrange strain is approximated by the
infinitesimal strain
The Cauchy, nominal and material stress are
assumed to be identical
The linear momentum balance equation
(expressed in terms of nominal stress) can then be expressed as
The
constitutive relations are simplified by expressing the free energy, stress,
and heat transfer response functions in terms of infinitesimal strain. The material behavior is characterized by the
following functions:
Specific Helmholtz free energy
Strain energy density (Helmholtz free
energy per unit volume)
Stress response function
Heat flux response function
They are related by
where we have noted that
In addition, the stress response function is linearized (expand it as a Taylor
series in ,
retaining only the second term and noting that the reference configuration is
stress free)
Here, the and
are constants (
is called the isothermal elastic stiffness
tensor)
the values of the constants are material
properties. They have the following
symmetries (because of the symmetry of the second derivative of U and the stress and strain tensors)
so
a general anisotropic material is characterized by 27 material properties (21
for , and 6 for
).
The contribution to the stress associated with changing the temperature (at fixed strain) is often written in a different form by defining the thermal expansion coefficient which satisfies
The thermal expansion can be visualized physically as the strain induced by a temperature change in a stress free solid. The constitutive law then has the form
A linear elasticity problem can be stated as follows:
1.
The shape of the
solid in its unloaded condition
2.
The initial stress field in the solid (we will take
this to be zero)
3.
The elastic
constants for the solid and its mass density
4. The thermal expansion coefficients for the solid, and
temperature change from the initial configuration
5. A body force distribution (per unit mass) acting on the solid
6. Boundary conditions, specifying displacements on a portion
or tractions on a portion
of the boundary of R
Calculate displacements, strains and stresses satisfying the governing equations of linear elastostatics
Dynamic problems Dynamic problems are essentially identical, except that the boundary conditions must be specified as functions of time, and the initial displacement and velocity field must be specified. In this case the governing equations are
These
field equations can be solved fairly easily a few solutions are listed in Section
8.13. These solutions are very useful,
but it is important to note that linearizing the field equations does eliminate
some physical behavior that can be important.
In particular, the linear momentum balance equation takes derivatives
with respect to position in the reference configuration
this means that the equation does not account
correctly for re-distributions of stress caused by changing the shape of the
solid. As a result, geometric
instability, such as buckling, cannot occur.
8.12 Linear elastic material properties
The symmetries of the elastic stiffness tensor allow us to write the stress-strain relations in a more compact matrix form as
where ,
etc are the elastic stiffnesses of
the material. The inverse has the form
where ,
etc are the elastic compliances of
the material.
To satisfy Drucker stability, the eigenvalues of the elastic stiffness and compliance matrices must all be greater than zero.
HEALTH WARNINGS: Note the factor of 2 in the strain vector. Most texts, and most FEM codes use this factor of two, but not all. In addition, shear strains and stresses are often listed in a different order in the strain and stress vectors. For isotropic materials this makes no difference, but you need to be careful when listing material constants for anisotropic materials (see below). In addition, the shear strain and shear stress components are not always listed in the order given when defining the elastic and compliance matrices. The conventions used here are common and are particularly convenient in analytical calculations involving anisotropic solids. But many sources use other conventions. Be careful to enter material data in the correct order when specifying properties for anisotropic solids.
Physical Interpretation of the Anisotropic Elastic Constants.
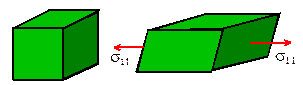It is easiest to interpret ,
rather than
. Imagine applying a uniaxial stress, say
,
to an anisotropic specimen. In general,
this would induce both extensional and shear deformation in the solid, as shown
in the figure.
The strain induced by the uniaxial stress would be
All the constants have dimensions . The constant
looks like a uniaxial compliance, (like
), while the ratios
are generalized versions of Poisson’s ratio:
they quantify the lateral contraction of a uniaxial tensile specimen. The shear terms are new
in an isotropic material, no shear strain is
induced by uniaxial tension.
Isotropic Materials
The
stress-strain laws can be simplified considerably for isotropic materials. In this case
The inverse relationship can be expressed as
Here,
E and are Young’s modulus and Poisson’s ratio,
is the coefficient of thermal expansion, and
is the increase in temperature of the
solid. The remaining relations can be
deduced from the fact that both
and
are symmetric.
Young’s modulus and Poisson’s ratio are
the most common properties used to characterize elastic solids, but other
measures are also used. For example, we
define the shear modulus, bulk
modulus and Lame modulus of an
elastic solid as follows:
We can write the linear elastic stress-strain relations in a much more convenient form using index notation. Verify for yourself that the matrix expression above is equivalent to
The inverse relation is
The stress-strain relations are often expressed using the elastic modulus tensor or the elastic
compliance tensor
as
In terms
of elastic constants, and
are
8.14 Reduced field equations for isotropic, linear elastic solids
The governing equations can be simplified by eliminating stress and strain from the governing equations, and solving directly for the displacements. In this case the linear momentum balance equation (in terms of displacement) reduces to
For
the special case of an isotropic solid with shear modulus and Poisson ratio
and uniform temperature
this equation reduces to
These are known as the Navier (or Cauchy-Navier) equations of elasticity.
The boundary conditions remain as given in Section 8.12.
8.15 Solutions to simple static linear elastic boundary value problems
The linearized equations of elasticity can be solved relatively easily. Further courses will describe the various techniques in more detail, but we list a few examples to give a sense of the general structure of linear elastic solutions.
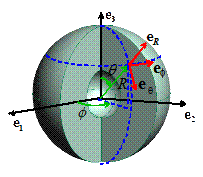Spherically
symmetric problems: A representative spherically symmetric problem is
illustrated in the picture. We consider
a hollow, spherical solid, which is subjected to spherically symmetric loading
(i.e. internal body forces, as well as tractions or displacements applied to
the surface, are independent of and
,
and act in the radial direction only).
If the temperature of the sphere is non-uniform, it must also be
spherically symmetric (a function of R
only).
The solution is most conveniently expressed using a spherical-polar coordinate system, illustrated in the figure. The general procedure for solving problems using spherical and cylindrical coordinates is complicated, and is discussed in detail in Appendix E. In this section, we summarize the special form of these equations for spherically symmetric problems.
As usual, a point in the solid is identified by its
spherical-polar co-ordinates .
All vectors and tensors are expressed as components in the basis
shown in the figure. For a spherically symmetric problem
Position Vector
Displacement
vector
Body
force vector
Here,
and
are scalar functions. The stress and strain
tensors (written as components in
) have the form
and
furthermore must satisfy
.
The tensor components have exactly the same physical interpretation as they did
when we used a fixed
basis, except that the subscripts (1,2,3) have
been replaced by
.
For spherical symmetry, the governing equations of linear elasticity reduce to
Strain Displacement Relations
StressStrain
relations
Equilibrium Equations
Boundary Conditions
Prescribed Displacements
Prescribed Tractions
Our goal is to solve these equations for the displacement, strain and stress in the sphere. To do so,
1. Substitute the strain-displacement relations into the stress-strain law to show that
2. Substitute this expression for the stress into the equilibrium equation and rearrange the result to see that
Given the temperature distribution and body force this
equation can easily be integrated to calculate the displacement u.
Two arbitrary constants of integration will appear when you do the
integral these must be determined from the boundary conditions at the inner and
outer surface of the sphere.
Specifically, the constants must be selected so that either the
displacement or the radial stress have prescribed values on the inner and outer
surface of the sphere.
In the following sections, this procedure is used to derive solutions to various boundary value problems of practical interest.
Pressurized
hollow sphere Assume that
No body forces act on the sphere
The sphere has uniform temperature
The inner surface R=a is subjected to pressure
The outer surface R=b is subjected to pressure
The displacement, strain and stress fields in the sphere are
Derivation: The solution can be found by applying the procedure outlined in Sect 4.1.3.
1. Note that the governing equation for u (Sect 4.1.3) reduces to
2. Integrating twice gives
where A and B are constants of integration to be determined.
3. The radial stress follows by substituting into the stress-displacement formulas
4. To satisfy the boundary conditions, A and B must be chosen so that and
(the stress is negative because the pressure
is compressive). This gives two
equations for A and B that are easily solved to find
5. Finally, expressions for displacement, strain and stress follow by substituting for A and B in the formula for u in (2), and using the formulas for strain and stress in terms of u .
General 3D static problems: Just as some fluid mechanics problems can be solved by deriving the velocity field from a scalar potential, a similar approach can be used to solve elasticity problems. In 3D, a common approach is to derive the solution from so-called Papkovich-Neuber potentials as follows
The Papkovich-Neuber procedure can be summarized as follows:
1. Begin by finding a vector function and scalar function
which satisfy
as well as boundary conditions
2. Calculate displacements from the formula
3. Calculate stresses from the formula
To see why this procedure works, we need to show two things:
1. That the displacement field satisfies the equilibrium equation
2. That the stresses are related to the displacements by the elastic stress-strain equations
To show the first result, differentiate the formula relating potentials to the displacement to see that
Substitute this result into the governing equation to see that
Finally, substitute the governing equations for the potentials
and simplify the result to verify that the governing equation is indeed satisfied. The second result can be derived by substituting the formula for displacement into the elastic stress-strain equations and simplifying.
Point force in an infinite solid. The displacements and stresses induced by a point
force acting at the origin of a large (infinite)
elastic solid with Young’s modulus E
and Poisson’s ratio
are generated by the Papkovich-Neuber
potentials
where .
The displacements, strains and stresses follow as
Point force normal to the surface of an
infinite half-spa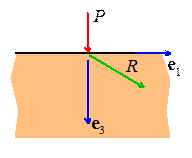ce
. The displacements and stresses induced by a point
force acting normal to the surface of a
semi-infinite solid with Young’s modulus E
and Poisson’s ratio
are generated by the Papkovich-Neuber
potentials
where
The displacements and stresses follow as
Point force tangent to the surface of an
infinite half-spa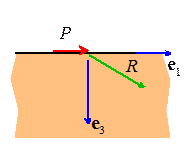ce
. The displacements and stresses induced by a point
force acting tangent to the surface of a
semi-infinite solid with Young’s modulus E
and Poisson’s ratio
are generated by the Papkovich-Neuber
potentials
The displacements and stresses can be calculated from these potentials as
Spherical cavity in an infinite solid
subjected to remote stress
. The figure shows a spherical cavity with radius a in an infinite, isotropic linear
elastic solid. Far from the cavity, the solid is subjected to a tensile stress ,
with all other stress components zero.
The solution is generated by potentials
The displacements and stresses follow as
8.15 Solutions to simple dynamic elasticity problems
In this section we summarize and derive the solutions to various elementary problems in dynamic linear elasticity.
Surface subjected to time varying normal
pressure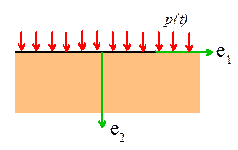
An
isotropic, linear elastic half space with shear modulus and Poisson’s ratio
and mass density
occupies the region
. The
solid is at rest and stress free at time t=0. For t>0 it is subjected to a
uniform pressure p(t) on
as shown in the picture.
Solution: The displacement and stress fields in the solid (as a function of time and position) are
where
is the speed of longitudinal wave propagation
through the solid. All other
displacement and stress components are zero.
For the particular case of a constant (i.e. time independent) pressure,
magnitude
,
applied to the surface
Evidently,
a stress pulse equal in magnitude to the surface pressure propagates vertically
through the half-space with speed .
Notice
that the velocity of the solid is constant in the region ,
and the velocity is related to the pressure by
Derivation: The solution can be derived as follows. The governing equations are
The strain-displacement relation
The
elastic stress-strain equations
The linear momentum balance equation
Now:
1. Symmetry considerations indicate that the displacement field must have the form
Substituting this equation into the strain-displacement
equations shows that the only nonzero component of strain is .
2. The stress-strain law then shows that
In addition, the shear stresses are all zero (because
the shear strains are zero), and while are nonzero, they are independent of
and
.
3. The only nonzero linear momentum balance equation is therefore
Substituting for stress from (2) yields
where
4. This is a 1-D wave equation with general solution
where f and g are two functions that must be chosen to satisfy boundary and initial conditions.
5. The initial conditions are
where the prime denotes differentiation with respect
to its argument. Solving these equations
(differentiate the first equation and then solve for and integrate) shows that
where A is some constant.
6. Observe that for t>0, so that
. Substituting this result back into the
solution in (4) gives
.
7. Next, use the
boundary condition at
to see that
where B is a constant of integration.
8.
Finally, B can be determined by setting t=0 in the result of (7) and recalling
from step (5) that . This shows that B=-A and so
as stated.
Surface
subjected to time varying shear traction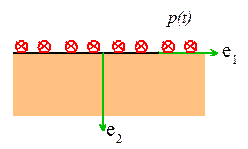
An
isotropic, linear elastic half space with shear modulus and Poisson’s ratio
and mass density
occupies the region
. The
solid is at rest and stress free at time t=0. For t>0 it is subjected to a
uniform anti-plane shear traction p(t) on
. Calculate the displacement, stress and strain
fields in the solid.
It is straightforward to show that in this case
where is the speed of shear waves propagating
through the solid. The details are left
as an exercise.
Plane waves in an infinite solid A plane wave that travels in direction p at speed c has a displacement field of the form
where p is a unit vector. Again, to visualize this motion, consider the special case
In
this solution, the wave has a planar front, with normal vector p. The wave travels in direction p at
speed c. Ahead of the front, the solid is at
rest. Behind it, the solid has velocity a. For the particle velocity is perpendicular to
the wave velocity. For
the particle velocity is parallel to the wave
velocity. These two cases are like the
shear and longitudinal waves discussed in the preceding sections.
We seek plane wave solutions of the Cauchy-Navier equation of motion
Substituting a plane wave solution for u we see that
where
is a symmetric, positive definite tensor known as the `Acoustic Tensor.’ Plane wave solutions to the Cauchy-Navier equation must therefore satisfy
This requires
Evidently
for any wave propagation direction, there are three wave speeds, and three
corresponding displacement directions, which follow from the eigenvalues and
eigenvectors of For the special case of an isotropic solid
where is the shear modulus and
is the Poisson’s ratio of the solid. The acoustic tensor follows as
so that
By inspection, there are two eigenvectors that satisfy this equation
1. (Shear wave, or S-wave)
2. (Longitudinal, or P-wave)
The
two wave speeds are evidently those we found in our 1-D calculation
earlier. So there are two types of plane
wave in an isotropic solid. The S-wave
travels at speed ,
and material particles are displaced
perpendicular to the direction of motion of the wave. The P-wave travels at speed
,
and material particles are displaced parallel to the direction of motion of the
wave.