2. Review of Vectors and Matrices
VECTORS
1. Definition
For
the purposes of this course, a vector is an object which has magnitude and
direction. Examples include forces,
electric fields, and the normal to a surface.
A vector is often represented pictorially as an arrow and symbolically
by an underlined letter or using bold type . Its magnitude is denoted or . There are two special cases of vectors: the unit vector has ;
and the null vector has .
2. Vector Operations
 Addition
Addition
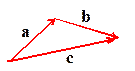 Let and be vectors.
Then is also a vector. The vector may be shown diagramatically by placing arrows
representing and head to tail, as shown in the figure.
Let and be vectors.
Then is also a vector. The vector may be shown diagramatically by placing arrows
representing and head to tail, as shown in the figure.
 Multiplication
Multiplication
1. Multiplication by a scalar. Let be a vector, and a scalar.
Then is a vector.
The direction of is parallel to and its magnitude is given by .
Note that you can form a unit vector n
which is parallel to a by setting .
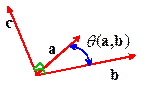
2.  Dot Product (also called the scalar product). Let a and b be two vectors. The dot
product of a and b is a scalar denoted by ,
and is defined by
Dot Product (also called the scalar product). Let a and b be two vectors. The dot
product of a and b is a scalar denoted by ,
and is defined by
,
where
is the angle subtended by a and b. Note that ,
and . If and then if and only if ;
i.e. a and b are perpendicular.
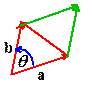
3.  Cross
Product (also called the vector
product). Let a and b be two
vectors. The cross product of a and b is a vector denoted by . The direction of c is perpendicular to a
and b, and is chosen so that (a,b,c) form a right handed triad, Fig.
3. The magnitude of c is given by
Cross
Product (also called the vector
product). Let a and b be two
vectors. The cross product of a and b is a vector denoted by . The direction of c is perpendicular to a
and b, and is chosen so that (a,b,c) form a right handed triad, Fig.
3. The magnitude of c is given by
Note
that and .
 Some useful vector identities
Some useful vector identities
3. Cartesian components of vectors
Let
be three mutually perpendicular unit vectors
which form a right handed triad, Fig. 4.
Then are said to form and orthonormal basis. The
vectors satisfy
We
may express any vector a as a
suitable combination of the unit vectors ,
and . For example, we may write
where
are scalars, called the components of a in the
basis . The components of a have a simple physical interpretation. For example, if we evaluate the dot product we find that
in view of the properties
of the three vectors ,
and . Recall that
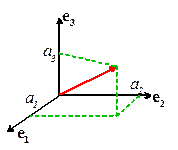
Then, noting that ,
we have
Thus,
represents the projected length of the vector a
in the direction of ,
as illustrated in the figure. Similarly,
and may be shown to represent the projection of in the directions and ,
respectively.
The
advantage of representing vectors in a Cartesian basis is that vector addition
and multiplication can be expressed as simple operations on the components of
the vectors. For example, let a, b
and c be vectors, with components ,
and ,
respectively. Then, it is
straightforward to show that
4. Change of basis
Let
a be a vector, and let be a Cartesian basis. Suppose that the components of a in the basis are known to be . Now, suppose that we wish to compute the
components of a in a second
Cartesian basis, . This means we wish to find components ,
such that
To do so, note that
This transformation is
conveniently written as a matrix operation
,
where
is a matrix consisting of the components of a in the basis ,
is a matrix consisting of the components of a in the basis ,
and is a `rotation matrix’ as follows
Note
that the elements of have a simple physical interpretation. For example, ,
where is the angle between the and axes.
Similarly where is the angle between the and axes.
In practice, we usually know the angles between the axes that make up
the two bases, so it is simplest to assemble the elements of by putting the cosines of the known angles in
the appropriate places.
Index notation provides
another convenient way to write this transformation:
You
don’t need to know index notation in detail to understand this all you need to know is that
The same approach may be
used to find an expression for in terms of . If you work through the details, you will
find that
Comparing this result with
the formula for in terms of ,
we see that
where
the superscript T denotes the
transpose (rows and columns interchanged). The transformation matrix is therefore orthogonal, and satisfies
where [I] is the identity matrix.
5. Useful vector operations
 Calculating areas
Calculating areas
The
area of a triangle bounded by vectors a,
b¸and b-a is
The
area of the parallelogram shown in the picture is 2A.
 Calculating
angles
Calculating
angles
The angle between two vectors a and b is
 Calculating
the normal to a surface.
Calculating
the normal to a surface.
If two vectors a and b can be found
which are known to lie in the surface, then the unit normal to the surface is
If the surface is specified by a
parametric equation of the form ,
where s and t are two parameters and
r is the position vector of a point
on the surface, then two vectors which lie in the plane may be computed from
 Calculating
Volumes
Calculating
Volumes
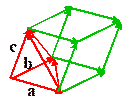
The volume of the parallelopiped defined by three vectors a, b,
c is
The volume of the tetrahedron shown outlined in red is V/6.
VECTOR FIELDS
AND VECTOR CALCULUS
1. Scalar field.
Let be a Cartesian basis with origin O in three
dimensional space. Let
denote
the position vector of a point in space.
A scalar field is a scalar
valued function of position in space. A
scalar field is a function of the components of the position vector, and so may
be expressed as .
The value of at a particular point in space must be
independent of the choice of basis vectors.
A scalar field may be a function of time (and possibly other parameters)
as well as position in space.
2. Vector field
Let be a Cartesian basis with origin O in three
dimensional space. Let
denote
the position vector of a point in space.
A vector field is a vector
valued function of position in space. A
vector field is a function of the components of the position vector, and so may
be expressed as . The vector may also be expressed as
components in the basis
The
magnitude and direction of at a particular point in space is independent
of the choice of basis vectors. A
vector field may be a function of time (and possibly other parameters) as well
as position in space.
3. Change of basis for scalar fields.
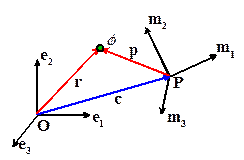
Let
be a Cartesian basis with origin O in three
dimensional space. Express the position vector of a point relative to O in as
and let be a scalar field.
Let
be a second Cartesian basis, with origin
P. Let denote the position vector of P relative to O. Express the position vector
of a point relative to P in as
To
find ,
use the following procedure. First,
express p as components in the basis ,
using the procedure outlined in Section 1.4:
where
or, using index notation
where the transformation
matrix is defined in Sect 1.4.
Now, express c as components in ,
and note that
so that
4. Change of basis for vector fields.

Let
be a Cartesian basis with origin O in three
dimensional space. Express the position vector of a point relative to O in as
and let be a vector
field, with components
Let
be a second Cartesian basis, with origin
P. Let denote the position vector of P relative to O. Express the position vector
of a point relative to P in as
To
express the vector field as components in and as a function of the components of p, use the following procedure. First, express in terms of using the procedure outlined for scalar fields
in the preceding section
for
k=1,2,3. Now, find the components of v
in using the procedure outlined in Section
1.4. Using index notation, the result is
5. Time derivatives of vectors
Let
a(t) be a vector whose magnitude and
direction vary with time, t. Suppose that is a fixed basis, i.e. independent of
time. We may express a(t)
in terms of components in the basis as
.
The time derivative of a is defined using the usual rules of
calculus
,
or in component form as
The
definition of the time derivative of a vector may be used to show the following
rules
6. Using a rotating basis
It
is often convenient to express position vectors as components in a basis which
rotates with time. To write equations of
motion one must evaluate time derivatives of rotating vectors.
Let be a basis which rotates with instantaneous
angular velocity . Then,
7. Gradient of a scalar field.
Let
be a scalar field in three dimensional
space. The gradient of is a vector field denoted by or ,
and is defined so that
for every position r in space and for every vector a.
Let be a Cartesian basis with origin O in three
dimensional space. Let
denote
the position vector of a point in space.
Express as a function of the components of r . The gradient of in this basis is then given by
8. Gradient of a vector field
Let v be a vector field in three dimensional space. The gradient of v is a tensor field denoted by or ,
and is defined so that
for every position r in space and for every vector a.
Let be a Cartesian basis with origin O in three
dimensional space. Let
denote
the position vector of a point in space.
Express v as a function of
the components of r, so that . The gradient of v
in this basis is then given by
Alternatively, in index
notation
9. Divergence of a vector field
Let
v be a vector field in three
dimensional space. The divergence of v is a scalar field denoted by or . Formally, it is defined as (the trace of a tensor is the sum of its
diagonal terms).
Let be a Cartesian basis with origin O in three
dimensional space. Let
denote
the position vector of a point in space.
Express v as a function of
the components of r: .
The divergence of v is then
10. Curl of a vector field.
Let
v be a vector field in three
dimensional space. The curl of v is a vector field denoted by or . It is best defined in terms of its components
in a given basis, although its magnitude and direction are not dependent on the
choice of basis.
Let be a Cartesian basis with origin O in three
dimensional space. Let
denote
the position vector of a point in space.
Express v as a function of
the components of r .
The curl of v in this basis is then given by
Using index notation, this
may be expressed as
11. The Divergence Theorem.
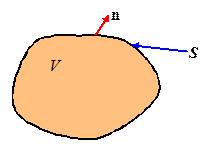
Let
V be a closed region in three
dimensional space, bounded by an orientable surface S. Let n denote the unit vector normal to S, taken so that n points out of V. Let u be a vector field which is continuous
and has continuous first partial derivatives in some domain containing T. Then
alternatively, expressed in
index notation
For
a proof of this extremely useful theorem consult e.g. Kreyzig, Advanced Engineering Mathematics, Wiley, New York, (1998).
MATRICES
1. Definition
An matrix is a set of numbers, arranged in m rows and n columns
 A square
matrix has equal numbers of rows and columns
A square
matrix has equal numbers of rows and columns
 A diagonal
matrix is a square matrix with elements such that for
A diagonal
matrix is a square matrix with elements such that for
 The identity
matrix is a diagonal matrix for which all diagonal
elements
The identity
matrix is a diagonal matrix for which all diagonal
elements
 A symmetric
matrix is a square matrix with elements such that
A symmetric
matrix is a square matrix with elements such that
 A skew
symmetric matrix is a square matrix with elements such that
A skew
symmetric matrix is a square matrix with elements such that
2. Matrix operations
 Addition Let and be two matrices of order with elements and . Then
Addition Let and be two matrices of order with elements and . Then
 Multiplication
by a scalar. Let be a matrix with elements ,
and let k be a scalar. Then
Multiplication
by a scalar. Let be a matrix with elements ,
and let k be a scalar. Then
 Multiplication by a matrix. Let be a matrix of order with elements ,
and let be a matrix of order with elements . The product is defined only if n=p, and is an matrix such that
Multiplication by a matrix. Let be a matrix of order with elements ,
and let be a matrix of order with elements . The product is defined only if n=p, and is an matrix such that
Note that
multiplication is distributive and associative, but not commutative, i.e.
The multiplication of a vector by a matrix is a particularly
important operation. Let b and c be two vectors with n components, which we think of as matrices.
Let be an matrix.
Thus
Now,
i.e.
 Transpose.
Let be a matrix of order with elements . The transpose of is denoted . If is an matrix such that ,
then ,
i.e.
Transpose.
Let be a matrix of order with elements . The transpose of is denoted . If is an matrix such that ,
then ,
i.e.
Note that
 Determinant The determinant is defined only for a square
matrix. Let be a matrix with components . The determinant of is denoted by or and is given by
Determinant The determinant is defined only for a square
matrix. Let be a matrix with components . The determinant of is denoted by or and is given by
Now, let be an matrix.
Define the minors of as the determinant formed by omitting the ith row and jth column of . For example, the minors and for a matrix are computed as follows. Let
Then
Define the cofactors of as
Then, the
determinant of the matrix is computed as follows
The result is the same whichever row i is chosen for the expansion.
For the particular case of a matrix
The determinant may also be
evaluated by summing over rows, i.e.
and as
before the result is the same for each choice of column j. Finally, note that
 Inversion. Let be an matrix.
The inverse of is denoted by and is defined such that
Inversion. Let be an matrix.
The inverse of is denoted by and is defined such that
The inverse of exists if and only if . A matrix which has no inverse is said to be singular. The inverse of a matrix may be computed
explicitly, by forming the cofactor
matrix with components as defined in the preceding section. Then
In practice, it is faster to compute the inverse of a matrix
using methods such as Gaussian elimination.
Note that
For a diagonal matrix, the inverse is
For a matrix, the inverse is
 Eigenvalues and eigenvectors. Let be an matrix, with coefficients . Consider the vector equation
Eigenvalues and eigenvectors. Let be an matrix, with coefficients . Consider the vector equation
(1)
where x is a vector with n
components, and is a scalar (which may be complex). The n
nonzero vectors x and corresponding
scalars which satisfy this equation are the eigenvectors and eigenvalues of .
Formally, eighenvalues and eigenvectors may be computed as
follows. Rearrange the preceding
equation to
(2)
This has nontrivial solutions for x only if the determinant of
the matrix vanishes.
The equation
is
an nth order polynomial which may be
solved for . In general the polynomial will have n roots, which may be complex. The eigenvectors may then be computed using
equation (2). For example, a matrix generally has two eigenvectors, which
satisfy
Solve the
quadratic equation to see that
The two
corresponding eigenvectors may be computed from (2), which shows that
so that, multiplying out the first row of the matrix (you can
use the second row too, if you wish since we chose to make the determinant of the matrix vanish,
the two equations have the same solutions.
In fact, if ,
you will need to do this, because the first equation will simply give 0=0 when
trying to solve for one of the eigenvectors)
which are satisfied
by any vector of the form
where p and q are arbitrary real numbers.
It is often convenient to normalize
eigenvectors so that they have unit `length’.
For this purpose, choose p and q so
that . (For vectors of dimension n, the generalized dot product is
defined such that )
One
may calculate explicit expressions for eigenvalues and eigenvectors for any
matrix up to order ,
but the results are so cumbersome that, except for the results, they are virtually useless. In practice, numerical values may be computed
using several iterative techniques.
Packages like Mathematica, Maple or Matlab make calculations like this
easy.
The
eigenvalues of a real symmetric matrix are always real, and its eigenvectors
are orthogonal, i.e. the ith and jth eigenvectors (with ) satisfy .
The eigenvalues of a skew
symmetric matrix are pure imaginary.
 Spectral
and singular value decomposition.
Let be a real symmetric matrix. Denote the n (real) eigenvalues of by ,
and let be the corresponding normalized eigenvectors, such that . Then, for any arbitrary vector b,
Spectral
and singular value decomposition.
Let be a real symmetric matrix. Denote the n (real) eigenvalues of by ,
and let be the corresponding normalized eigenvectors, such that . Then, for any arbitrary vector b,
Let be a diagonal matrix which contains the n
eigenvalues of as elements of the diagonal, and let be a matrix consisting of the n eigenvectors as columns, i.e.
Then
Note that this gives
another (generally quite useless) way to invert
where is easy to compute since is diagonal.
 Square
root of a matrix. Let be a real symmetric matrix.
Denote the singular value decomposition of by as defined above. Suppose that denotes the square root of ,
defined so that
Square
root of a matrix. Let be a real symmetric matrix.
Denote the singular value decomposition of by as defined above. Suppose that denotes the square root of ,
defined so that
One way to
compute is through the singular value decomposition of
where
![]() Addition
Addition Let and be vectors.
Then is also a vector. The vector may be shown diagramatically by placing arrows
representing and head to tail, as shown in the figure.
Let and be vectors.
Then is also a vector. The vector may be shown diagramatically by placing arrows
representing and head to tail, as shown in the figure.![]() Multiplication
Multiplication Dot Product (also called the scalar product). Let a and b be two vectors. The dot
product of a and b is a scalar denoted by ,
and is defined by
Dot Product (also called the scalar product). Let a and b be two vectors. The dot
product of a and b is a scalar denoted by ,
and is defined by Cross
Product (also called the vector
product). Let a and b be two
vectors. The cross product of a and b is a vector denoted by . The direction of c is perpendicular to a
and b, and is chosen so that (a,b,c) form a right handed triad, Fig.
3. The magnitude of c is given by
Cross
Product (also called the vector
product). Let a and b be two
vectors. The cross product of a and b is a vector denoted by . The direction of c is perpendicular to a
and b, and is chosen so that (a,b,c) form a right handed triad, Fig.
3. The magnitude of c is given by![]() Some useful vector identities
Some useful vector identities

![]() Calculating areas
Calculating areas![]() Calculating
angles
Calculating
angles![]() Calculating
the normal to a surface.
Calculating
the normal to a surface.![]() Calculating
Volumes
Calculating
Volumes



![]() A square
matrix has equal numbers of rows and columns
A square
matrix has equal numbers of rows and columns![]() A diagonal
matrix is a square matrix with elements such that for
A diagonal
matrix is a square matrix with elements such that for ![]() The identity
matrix is a diagonal matrix for which all diagonal
elements
The identity
matrix is a diagonal matrix for which all diagonal
elements ![]() A symmetric
matrix is a square matrix with elements such that
A symmetric
matrix is a square matrix with elements such that ![]() A skew
symmetric matrix is a square matrix with elements such that
A skew
symmetric matrix is a square matrix with elements such that ![]() Addition Let and be two matrices of order with elements and . Then
Addition Let and be two matrices of order with elements and . Then![]() Multiplication
by a scalar. Let be a matrix with elements ,
and let k be a scalar. Then
Multiplication
by a scalar. Let be a matrix with elements ,
and let k be a scalar. Then![]() Multiplication by a matrix. Let be a matrix of order with elements ,
and let be a matrix of order with elements . The product is defined only if n=p, and is an matrix such that
Multiplication by a matrix. Let be a matrix of order with elements ,
and let be a matrix of order with elements . The product is defined only if n=p, and is an matrix such that![]() Transpose.
Let be a matrix of order with elements . The transpose of is denoted . If is an matrix such that ,
then ,
i.e.
Transpose.
Let be a matrix of order with elements . The transpose of is denoted . If is an matrix such that ,
then ,
i.e.![]() Determinant The determinant is defined only for a square
matrix. Let be a matrix with components . The determinant of is denoted by or and is given by
Determinant The determinant is defined only for a square
matrix. Let be a matrix with components . The determinant of is denoted by or and is given by![]() Inversion. Let be an matrix.
The inverse of is denoted by and is defined such that
Inversion. Let be an matrix.
The inverse of is denoted by and is defined such that![]() Eigenvalues and eigenvectors. Let be an matrix, with coefficients . Consider the vector equation
Eigenvalues and eigenvectors. Let be an matrix, with coefficients . Consider the vector equation![]() Spectral
and singular value decomposition.
Let be a real symmetric matrix. Denote the n (real) eigenvalues of by ,
and let be the corresponding normalized eigenvectors, such that . Then, for any arbitrary vector b,
Spectral
and singular value decomposition.
Let be a real symmetric matrix. Denote the n (real) eigenvalues of by ,
and let be the corresponding normalized eigenvectors, such that . Then, for any arbitrary vector b, ![]() Square
root of a matrix. Let be a real symmetric matrix.
Denote the singular value decomposition of by as defined above. Suppose that denotes the square root of ,
defined so that
Square
root of a matrix. Let be a real symmetric matrix.
Denote the singular value decomposition of by as defined above. Suppose that denotes the square root of ,
defined so that