
EN4:
Dynamics and Vibrations
Division of Engineering
Brown University
2.4 Curvilinear motion of a particle I: Analyzing motion in a fixed basis
In the preceding section, we discussed techniques for determining the velocity and position of a particle from its acceleration. To keep things simple, we assumed that the particle moved along a straight line. We will now relax this assumption, and solve problems where the particle may travel along a curved path.
When dealing with particles that travel along a curved path, we need to describe position, velocity and acceleration as vectors. This means we need to find a convenient basis (a set of axes) to characterize our vectors.
We use two general approaches to do this. In some cases, it is best to choose a basis that is fixed in space. This approach should already be familiar to you. In other cases, it is preferable to use a basis that travels with the particle. The orientation of the basis is then determined by the position of the particle in space. We will discuss specific cases where this approach is useful later. To begin with, we will analyze curvilinear motion in a fixed basis.
Analyzing motion in a fixed basis
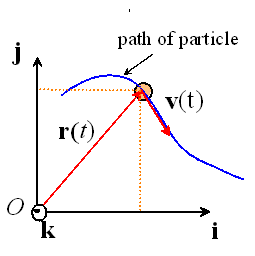
Let {i,j,k} be a fixed Cartesian basis, as shown in the picture. As discussed in section 2.1, we may express the position vector r, the velocity vector v and the acceleration vector a as components in this basis:
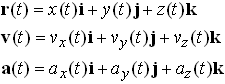
The vectors are related by
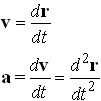
Since {i,j,k} do not vary with time, we only need to differentiate the components of r and v with respect to time, we do not have to differentiate the {i,j,k} vectors. Therefore, the components are related by
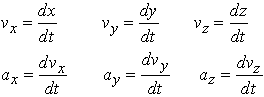
Now, consider the following problem. Suppose we are given the acceleration vector ![]() , and we are
also given values of v and r at time t=0. Determine v and r
for all time.
, and we are
also given values of v and r at time t=0. Determine v and r
for all time.
This turns out to be remarkably easy to do. We simply treat each component of
acceleration, velocity and position separately. Thus, to determine ![]() , we integrate
, we integrate ![]() , and to determine
, and to determine ![]() we integrate
we integrate ![]() , and so on.
, and so on.
Let’s illustrate this with an example.
Trajectory of a particle close to the earth’s surface
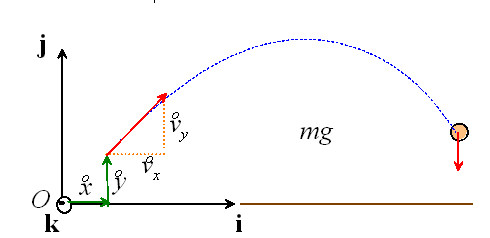
Suppose we launch a projectile from a point close to the surface of the earth. Let {i,j,k} be a Cartesian basis with origin on the ground and j vertical, as shown in the picture.
Assume that the particle is launched at time t=0 with velocity
![]()
from a position
![]()
Find the subsequent variation of velocity and position of the particle. Air resistance may be neglected.
Start by computing the acceleration of the particle. The particle is subjected to a
force ![]() due to gravity, whence
Newton’s second law shows that its acceleration is
due to gravity, whence
Newton’s second law shows that its acceleration is
![]() .
.
Now integrate all three acceleration components to determine the velocity:
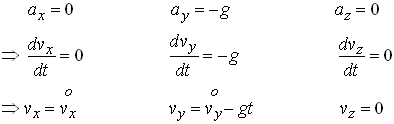
Next, integrate the velocity components to determine the position
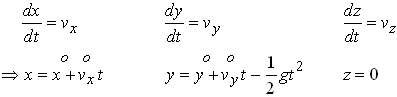
Summary:
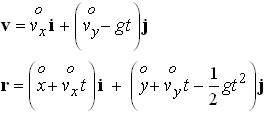
Exactly the same procedure can be used for different accelerations, as long as the acceleration is a function of time only. Many of the problems you will encounter in homeworks and exams (although not in real life) involve the trajectory example described above.
Example 1:
By this point in the semester, you may be considering switching to a career as a veterinarian. If so, the following problem will be of interest to you.
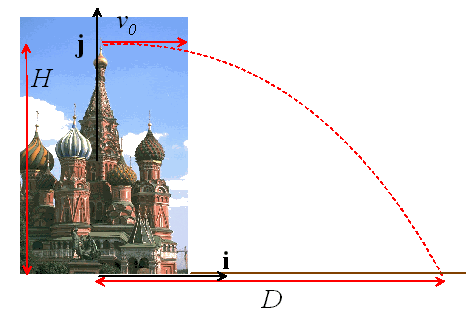
Suppose that you are in the jungle, attempting to immunize a monkey colony against the Ebola Reston virus. To do this, you shoot them with a tranquilizer dart, and then administer the vaccine. You have shot the monkeys so many times by now that they are developing ways to escape you. One of their tricks is to drop from the tree the moment you fire your tranquilizer dart.
Fortunately, as a result of your Brown education, you are marginally smarter than the monkey. Your mission, should you choose to accept it, is to determine the angle at which you should fire your dart, taking into account the fact that the monkey will drop from the tree the moment you pull the trigger.
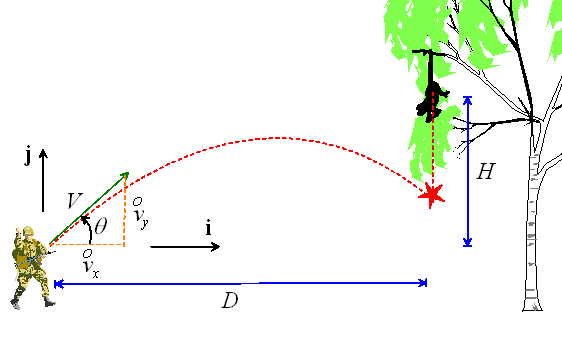
Suppose that the monkey is a distance D away from you, and a height H
above the muzzle of your gun. Assume that the dart leaves your gun at speed ![]() at an angle
at an angle
![]() to the horizontal, as shown
in the picture.
to the horizontal, as shown
in the picture.
To proceed, we need to find expressions for the position of the dart and the monkey as a function of time.
For the dart, the initial position and velocity are:
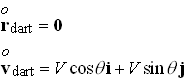
From the results in the preceding section, the dart’s position as a function of time is
![]()
Similarly, the monkey’s position and velocity at time t=0 are
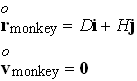
The results in the preceding section show that the monkey’s position as a function of time is
![]()
Now, we determine the angle ![]() from the condition that the dart must hit the monkey. This means that, at some time
from the condition that the dart must hit the monkey. This means that, at some time ![]() , the position of the dart is equal
to the position of the monkey. Therefore
, the position of the dart is equal
to the position of the monkey. Therefore
![]()
We now have two unknowns: the time of impact and the angle. Fortunately, the preceding vector equation is actually two equations: the i component on the left must equal the i component on the right; similarly, the j components must be equal. This shows that
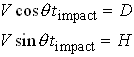
(we cancelled the terms involving the acceleration due to gravity). Divide the second equation by the first to see that
![]()
This is telling us that we should aim directly at the monkey! To see this, look at the picture below

In retrospect, this is obvious. Both the dart and the monkey are accelerated towards the ground at the same rate by gravity. We could remove the effects of gravity by solving the problem in an accelerating reference frame, which travels with the monkey. If there is no gravity, it is clear that you should aim directly at the monkey.
Most projectile motion problems are very similar to the monkey problem. You need to find the position and/or velocity of the projectile as a function of time, and then use the resulting equations to solve for unknowns of interest. Let’s look at another couple of examples:
Example 2: If a stone is thrown horizontally from the top of a 100 ft tall building at 50 ft/s, at what horizontal distance from point at which it is thrown will it hit the ground? What is the magnitude of its velocity just before it hits?
Take the origin as shown. Then:
![]()
From our general trajectory result
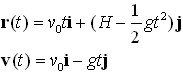
When the particle hits the ground, its position is
![]()
Hence, at the impact time ![]() :
:
![]()
The j component of this equation tells us that
![]()
Substituting for ![]() in the i component then shows that
in the i component then shows that
![]()
At the impact time, the velocity is
![]()
The magnitude of the velocity is therefore
![]()
Example 3: A projectile is launched at 10m/s from a sloping surface. Determine the range R.
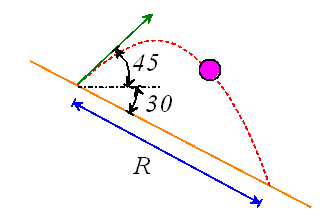
We will solve this problem using two approaches.
For our first approach, we will choose basis vectors parallel and perpendicular to the incline to describe vectors.
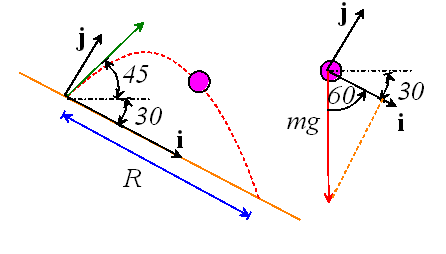
Introduce {i,j,k} basis vectors as shown. Express the force acting on the particle as components in this basis
![]()
Newton’s second law gives the acceleration as
![]()
The initial velocity components in this basis are
![]() ,
,
where V is the magnitude of the the initial velocity (10 m/s).
The initial position of the particle is ![]() .
.
Now, integrate the acceleration twice to determine the position of the particle (the acceleration is constant, so the integrals are easy to do)
![]()
Now, we see that when the particle impacts the plane, its position vector is
![]()
Therefore, if ![]() denotes the
time at which impact occurs
denotes the
time at which impact occurs
![]()
The i and j components of this vector equation give us two equations for
two unknowns: the impact time ![]() and the range R. Their solution is
and the range R. Their solution is
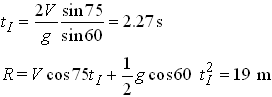
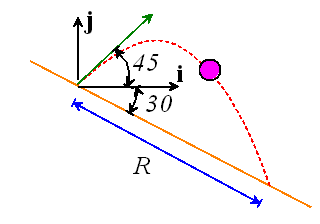
We will now solve the problem a slightly different way. This time, choose basis vectors {i,j,k} so that i and k are horizontal, and j is vertical. The components of initial velocity in this basis are
![]()
The initial position is ![]() .
We already have a general solution for the components of r in this basis:
.
We already have a general solution for the components of r in this basis:
![]()
When the particle hits the ramp, its position is
![]()
Consequently, at the time of impact
![]()
As before, this gives us two equations for R and ![]() , but solving them is a bit messier this time. Matching
i components on the left and right hand sides shows that
, but solving them is a bit messier this time. Matching
i components on the left and right hand sides shows that
![]()
Matching j components and substituting for ![]() shows that
shows that
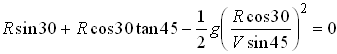
For V=10 m/s and ![]() this equation has solutions R=0 and R=19m, as before.
this equation has solutions R=0 and R=19m, as before.