EN4: Dynamics and Vibrations

 

  Division of Engineering
  Brown University

 

2.5 Angular motion

In the next section, we will discuss some more techniques for predicting the motion of a particle that travels along a curved path. In particular, we will show how to solve problems by expressing position, velocity and acceleration vectors as components in a rotating basis. We will see that this approach greatly simplifies many problems.

Before doing this, however, we need to discuss how we describe the rotational motion of a solid object. To this end, we will introduce the ideas of angular velocity and angular acceleration.

Definition of angular velocity

Look at the rotating solid shown below. You can see that it is rotating about an axis. The axis of rotation is a line of points in the body that do not move, like the hub of a wheel. In the picture shown, the box diagonal is the axis of rotation.

 

We describe the rotational motion of an object by specifying its angular velocity.

Angular velocity is a vector, and therefore has both magnitude and direction. In this course, we will generally use the symbol or to denote the angular velocity vector.

The magnitude of specifies the rate of rotation about the axis, in radians per second.

We sometimes specify rotation rates in terms of the number of revolutions of the object per minute (rpm). To compute the magnitude of , we would need to convert this to radians per second:

 

The direction of is parallel to the axis of rotation, following the right hand screw convention.

We could specify the direction of by choosing a unit vector p, which is parallel to the axis of rotation. For the rotating cube shown above, p would be vertical. Now, note that we have a problem. There are actually two unit vectors parallel to the axis of rotation: p could point straight up, or it could point straight down. Which one should we choose?

The right hand screw convention is introduced to resolve this issue. Suppose we look along the axis of rotation. Two such views of our cube are shown. On the left, we view the cube from above; on the right, we view it from below. In both cases we are looking along the axis of rotation.

 

If we are looking in the direction of p (i.e. the vector p points away from us) we should see the solid rotating clockwise. For our cube, this happens if we look along the axis from underneath the cube.

If we are looking in a direction opposite to p, (i.e. the vector p points towards us), we should see the solid rotating counterclockwise. For the cube, this happens of we look from above the cube.

Therefore, the correct direction for p in this case is vertically upwards.

 

What does this have to do with the right hand screw convention? Put your right hand in position as though you were about to begin sucking your thumb. Your thumb represents the angular velocity vector, pointing towards you. Your fingers curl in the direction of rotation of the solid object.

Some observations:

The angular velocity of a body is independent of its translational motion.

The axis of rotation of a body need not be inside the body itself.

For the example shown here, the axis of rotation does not vary with time (the cube always spins about its diagonal. In general, the axis of rotation may vary. At any instant, however, there is always an instantaneous axis of rotation, which defines the angular velocity vector.

To fix the idea of angular velocity, let’s look at a few examples

 

 

EXAMPLE I. Find the components of the angular velocity vector in the {i,j,k} basis shown for each hand of the clock.

The hands evidently rotate about an axis pointing out of the plane of the picture. We are therefore looking along the axis of rotation. We see each hand rotating clockwise, therefore the angular velocity vector points away from us. The direction of the angular velocity vector is therefore .

The second hand makes a complete revolution every minute. Its angular velocity is therefore

Similarly, the minute hand makes a complete revolution every hour. Its angular velocity is

We’ll leave the hour hand as an exercise…

 

 

EXAMPLE II. The hoop shown below rotates at an angular rate about the line AB, as shown. Write down its angular velocity.

The line AB is evidently in the j direction. If we were to look at the hoop from above (with j pointing towards us) we would see the hoop rotating counterclockwise. The angular velocity vector therefore points along the positive j direction. The angular velocity vector must be

 

 

EXAMPLE III. A particle travels around a circular path with speed v(t). Find the angular velocity of the radial line which points from the center of the circle to the particle. Express the answer as components in the basis shown.

The line OA rotates about an axis perpendicular to the plane of the picture. The line appears to rotate counterclockwise from our vantage point. The angular velocity vector therefore points towards us. The direction of the angular velocity vector is .

The rate of rotation of the line is evidently , where is the angle shown in the picture. We need to relate to v(t).

To do this, note that the distance traveled by the particle around the circumference of the circle is related to by

Therefore, differentiating,

Now, note that

and so

Finally, the angular velocity follows as

This is a very important result, which we will use later.

 

 

 

Angular Acceleration

While we are on the subject of rotational motion, we may as well introduce the idea of angular acceleration, which will be important in our discussion of rigid body motion.

We have seen that angular velocity is a vector, and may be expressed as

where p is a unit vector parallel to the axis of rotation (with the right hand screw convention) and is the rate of rotation about the axis in radians per second.

The angular acceleration vector, normally given the symbol , is the time derivative of the angular velocity.

We can differentiate the expression for to see that

(Here, we assumed without proof that . We’ll see why this is true later).

 

 

 

Angular acceleration – velocity – rotation relations for planar motion

Almost all the problems we solve in this course (although not in real life) involve particles or rigid bodies that move in a single plane.

Under these conditions, the direction p of the angular velocity vector does not vary with time. This situation resembles straight line motion – the rotational motion is always in the same direction.

If this is true, we can integrate angular acceleration to compute angular velocity, and integrate angular velocity to compute the angle of rotation, using exactly the same procedure that we discussed for straight line motion of a particle.

We will show this using an example.

 

 

Example: A needle of a measuring instrument is connected to a torsional spring that subjects it to an angular acceleration , where is the needle’s angular position in radians relative to a reference direction. If the needle is released from rest at , what is its angular velocity at ?

First, we notice that as increases, the needle rotates counterclockwise about an axis out of the plane of the picture. The angular velocity is therefore

The angular acceleration vector is

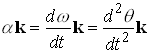
Now, we are told that , and that at time t=0, and . We are being asked to find an expression for as a function of .

To do this, observe that

by the chain rule. This is analogous to our `alternative expression for acceleration’ for the case of straight line motion.

Hence, for the problem at hand,

Why two solutions? This system behaves exactly like the--spring mass problem we solved earlier. The needle oscillates back and forth between . The velocity is positive when the needle is swinging one way, and negative when it is swinging in the opposite direction.