Non-linearity
and Infinite Performances
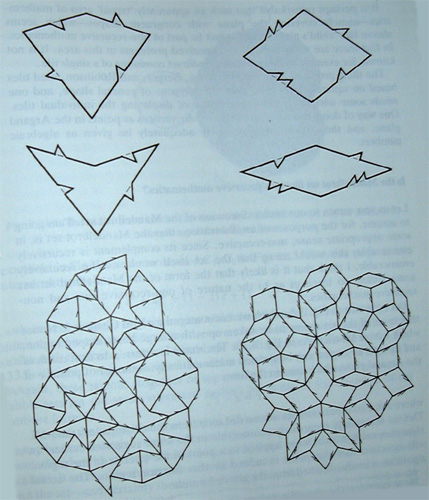
The above tiles were created by British Mathematician Robert Penrose, and can be fit together in a process that creates what is called an aperiodic pattern. Traditional tiles create patterns periodically, with multiple degrees of translational symmetry. In simple terms, the pattern repeats.
With aperiodic tiles, these degrees of symmetry are simply not present in their normal forms. Parts of the pattern almost repeat, but with slight variations. There are many common regions, but they are variations on a theme, rather than exact copies. Sometimes to fit a piece in without making a mistake, one has to step back and observe the whole pattern. Penrose refers to this characteristic as "non-local" patterning.
Aperiodic tiles create a perfect analogy for Eco's Open Work. With such a work, the author does not complete the work, but rather leaves some part of the creative process up to the interpreter or performer of the work. The author creates the tiles, and then the performer fits them together.
The tiling analogy seems particularly appropriate when discussing the openness of the works of Calvino. Nearly all of his works consists of these two disparate elements: a set of artistic tiles and a technique for fitting them together. Geometry, it seems, can be the basis for an open work.
img: Penrose Tiles, from The Emperor's New Mind, Roger Penrose