Hair Cell Biophysics, Semicircular canal mechanics
and VIII nerve responses
----------------
§
Reading
Hair Cells: A.J. Hudspeth:
"The hair cells of the inner ear", Scientific American, Jan 1983: 54-64
"The cellular basis of hearing: The biophysics of hair cells", Science
230: 745-752 (1985)
Nature 428: 901 (2004) review by Hudspeth's student David Corey, now at
Mass General, "Tightrope Act."
Semicircular Canal (SCC) Mechanics: Victor J. Wilson & Geoffrey
Melvill-Jones, Mammalian Vestibular Physiology, Plenum Press, 1979.
on reserve at Sci. Li., [QP471/W54]. Chapter 3, "Biophysics of peripheral end
organs."
RHSC2 chapter 2: "Vestibular eye movements".
Outline:
Anatomy & physiology hair cells & semicircular canals
Anatomy & structure of hair cells
Second order mechanics of hair cell deflection in the SCC
Hair cells can be found in the vertebrate cochlea, otolith, lateral
line, and the vestibular apparatus. In the semicircular canals (SCC) of the
vestibular system the hair cells are embedded in the cristae and protrude into
the cupula, which spans the canal at the enlargement of the ampula. In the canal
is endolymph fluid. The basal side of the hair cells contact by synapses fibers
of the VIII nerve. VIII projects into the brainstem, to the vestibular nuclei.
About 20,000 of the VIII fibers are due to the vestibular apparatus.
Viewgraphs from Hudspeth 1983:
anatomy of canal
ampulla widened region of canal
cupula the gelatinous mass + hairs
cristae "special region," like the maculae. it's the rise in the ampula
3 canals on each side: six all total!
For the vestibuloocular reflex we will concern ourselves with the two horizontal canals
Cilia on apical side of hair cell
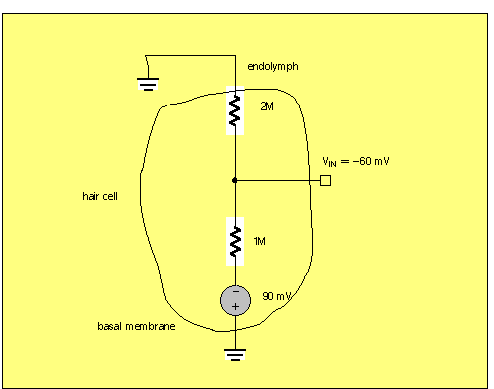
A close-up of a hair cell shows that it extends from the endolymph to the basal
membrane. The set of hair cells and support cells forms a complete barrier between
the two realms (endolymph and synaptic contact as base of hair cells). On the
endolymph side each hair cell has about 50 cilia in a hexagonal array, forming
a staircase assembly projecting up into the cupula. The array of cilia has an
orientation, because of one special stereocilium on one end. Of the thousands
of hair cells in any one cupula, all are oriented in the same direction with
respect to their stereocilia. It is the deflection of the hairs on the apical
membrane that is the mechanical event which causes the inside of the hair cell
to change voltage, and this changed voltage in turn causes more or less neurotransmitter
to be released onto the awaiting VIII fibers at the other end of the cell.
Hudspeth was able to isolate single hair cells and impale them with glass pipette recording electrodes. He measured intracellular voltage change as a function of mechanical deflection.
Endolymph and hair cell resting potential
The endolymph is a special fluid with a high potassium ion concentration, similar
to the intracellular potassium ion [K+] in the cytoplasm of the hair cell itself.
The other side of the hair cell, where synaptic contact is made with VIII nerve
fibers, has a membrane encountering a more standard low-K extracellular fluid. Because
of this basal membrane concentration gradient, there is a Nernst potential of (say)
-90mV internal.
[See en123 website, http://www.engin.brown.edu/courses/en123/Lectures/electrodes.htm
lecture notes on Electrodes, for more details. Qualitatively, imagine that K+ ions
diffuse from the inside to the outside, through membrane channels, leaving a deficit
of + charge on the inside of the cell].
In order to have a resting potential of about -60mV, there would need to be about twice the conductance at the basal membrane as there is at the endolymph membrane.

The mechanism of transduction
Only to the extent the central cilia are deflected along their axis with the lone
stereocilia does the haircell voltage change. If the cilia are deflected at right
angles to that axis, the hair cell intracellular voltage does not change at all.
This result is a clue about how the transduction takes place!
image below clipped from www.du.edu/~kinnamon/3640/
hearing/hearing.html
in turn copied from
Levitan and Kaczmarek, The Neuron, Figure 13-4...
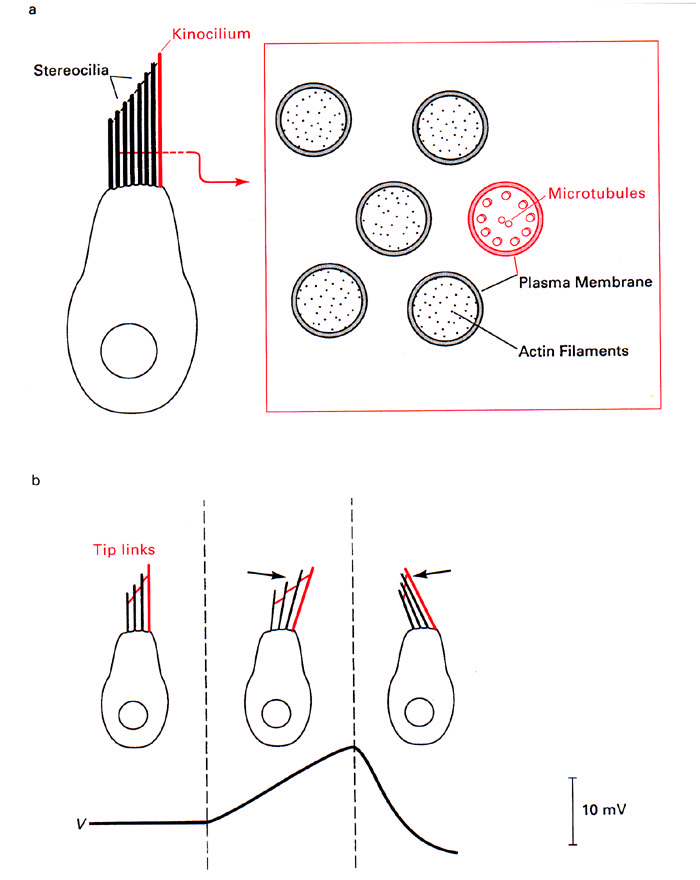
As you can see from other diagrams in Hudspeth's papers, current flow during transduction
is largest when sensed near the tips of the cilia, not when recorded at the
base of the cilia where it contacts the hair cell "body". The hypothesis
is: Protein filaments stretch from a longer cilia to it's "downstream"
shorter cilia neighbor. When the bundle is deflected in the direction of the stereocilia,
the filaments extend further and mechanically open channels that allow K+ to flow.
The hair cell potential becomes more positive (depolarized). See diagram above.
Such filaments have been seen at the electron microscope level.
DEMO:
[It is a change in the viscosity of endolymph that is a contributing factor
in the dizziness of inebriation. Enough EtOH mixes with the endolymph to lower
its viscosity.]
SCC mechanics: Time constants
First consider the endolymph fluid in the canal, as the canal begins to
rotate about its axis. Because of its rotational inertia, the fluid will attempt
to remain in place, but will be dragged along by viscous resistance of the canal
wall. Without for now worrying about the hair cells and cupula being in the
path of flow, what will be the time constant of the fluid reaction? We have
the following equation:
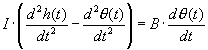
where h(t) is the position in time of head, and θ is the position of the
fluid w.r.t. the canal reference frame. In Laplace transform terms we have
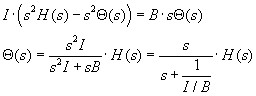
where an integration reduces the order of the equation. I/B is the time
constant, as could be concluded from prior work on first order diff. equations...remember
T=B/K in the derivation of the mechanical load of the eye.
We can calculate the rotational inertia of the fluid in the canal, assuming
a density of ρ=1, with r the inner radius and R the diameter of the
canal as a whole. Reasonable values for r and R are 0.16 mm and 3 mm.
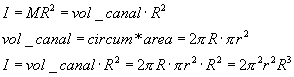
On p. 47 Wilson & Melvill-Jones(1979) derive drag coefficient B
of the whole canal length 2*pi*R, to be
![]()
ending up, with no dependence on the internal diameter r of the canal: see details
below:
------------------------------------------------------------------------
Details of Wilson p47 derivation of fluid drag coefficient:
Start with the Poiseuille-Hagen equation, which calculates the average
"volumetric flow" V (units are cm^3/sec) of a fluid with viscosity
η in a pipe of radius r, and length L, which experiences a pressure drop
ΔP,
![]()
Wilson recasts this equation in terms of force = pressure*area, coming up with
![]()
then Wilson wants the "turning moment" (torque) of this force:
![]()
B, the viscous drag coefficient, will end up in an equation T = B*Ω,
so we must extract Ω:
First, convert discharge J to velocity, with units cm/sec.
![]()
where dividing by the area of the canal leaves average "linear" velocity
of the fluid.
Since there are 2π radians per cycle, then one radian is R length and that
R will covered at a rate
Ω = v/R radians per seconds. Therefore
![]()
Now we can compute B:
![]()
and (curiously) small r has disappeared from the formula...
------------------------------------------------------------------------
Given the viscosity η of endolymph as 0.01 poise
(poise units are dyne-sec/cm^2, again, from Wilson & Melvill-Jones, Table 2.1),
we find
![]()
Net rotation of endolymph in canal, due to head rotation.
If the head rotation in radians, as a function of time, is described by h(t), and
the lagging rotation of the endolymph in the canal is θ(t), then the net rotation
of the endolymph in the skull is h(t) - θ(t). Considering the viscous
resistance of the endolymph in the canal, B, and the resisting stiffness K of the
cupula in the ampula of the canal, we have this differential equation, and its "solution"
in Laplace transform terms:
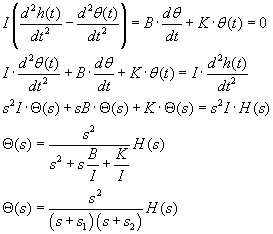
You can see one of the time constants, I/B, appears as the coefficient of s in one
form of the denominator.
Torsional spring stiffness of cupula and two time constants
How do we account for the value of the torsional spring stiffness of the
cupula (wherein lie the hair cells) in a second order equation? We know that
the cupula reacts to and resists the endolymph pressing against it during rotation.
But we have no straightforward way to calculate or measure directly the cupula
stiffness. What we can do is observe the response of the canal (by recording
activity on the VIII nerve) to a stimulus that isolates the time constants.
What stimulus h(t) has a Laplace transform that is 1/s^2? Recall the Laplace
transform of the impulse is 1, the Laplace transform of the integral of the
impulse, the step, is 1/s and the integral of the step: the ramp has Laplace
transform 1/s^2. So we drive the canal with a ramp function of rotation.
In the example below we illustrate what happens if s1 = 10 and s2 = 1, resulting
in a denominator of
![]()
Let's use s1=10, s2=1. In such a case s1+s2 ≈ s1, approx. Try the following
Simulink model:
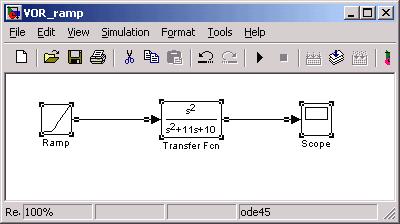
The scope shows:
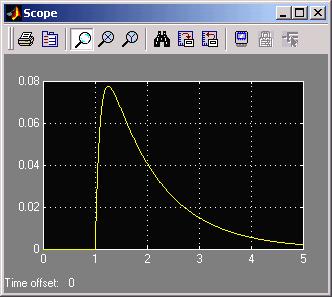
Where you can see the fast time constant (1/10) creates the rising edge and the
slow time constant (1 sec) dominates the falling edge of the waveform response to
the ramp. Notice the response returns to zero, since the ramp has a zero second
order derivative. What we have in the SCC is an accelerometer: responding to rotational
acceleration of the head.
Experimental results from VIII recordings suggest the other time constant is
much greater than 3msec, maybe about 3 sec, or 1000x larger. We can derive K
by the following, assuming s1 >> s2:
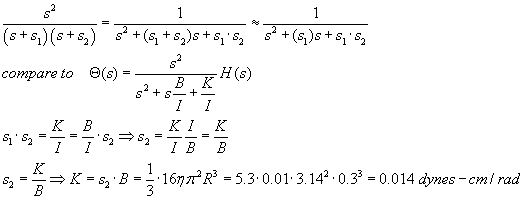
But really all we care about for purposes of simulation are the two time constants, 3 msec and 3 seconds...
Bode plot
What is the frequency response of the VIII nerve transfer function? As suggested
in Assgn 1B, you can type into the command line of Matlab, or into a Matlab script,
a frequency range and the exact complex number formulation of the transfer function
and ask Matlab to plot. Below is a version of such a plot where the time constants
used were 3 msec and 5 sec. (script Bode00.m)
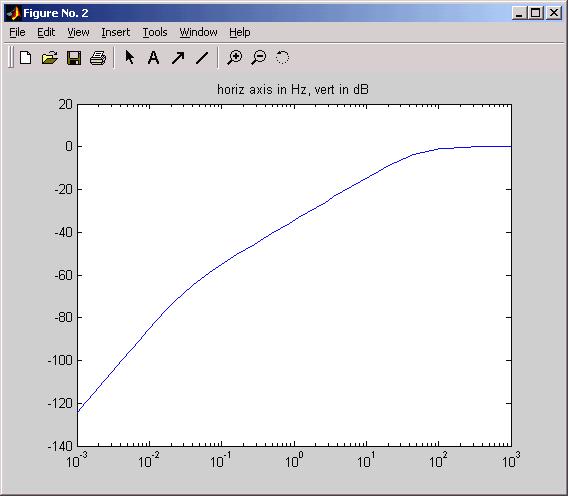
Notes: overall the SCC is a high pass filter. Script Bode00 has arranged that the
high frequency gain = 0 dB = gain of 1.00
At v. low freq's the slope of the curve is +40dB/decade, indicating a second-order
system (accelerometer) while in the "physiological range" of rotation
frequencies the slope is +20dB/dec: the range of the "velocity sensitive accelerometer".
It is the remaining s in the numerator of the transfer function in the physiological
range that the neural integrator in the final common path (OMN circuit) is designed
(evolved) to compensate.
Question: can you add to the Bode00 script to generate the phase vs frequency plot?
Summary
§
§