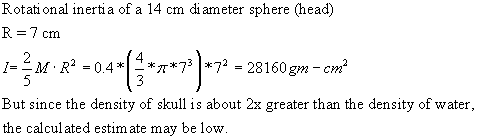Head and Eye Coordination
Reading: R.J. Leigh & D.S. Zee, The Neurology of Eye Movements
4th Ed, Oxford Press (2006) chapter 7
review below:
Animals that don't make eye movements, like birds, do make head movements.
(Pigeons making back-and-forth [surge] head movements while walking...)
Sidebar on bird head rotation: As noted in the first lecture
notes on "Why Make Eye Movements?", Birds have a minimum of 11 and
a maximum of 25 cervical vertebrae (humans have 7). LINK
to image
By "head movement" we mean neck muscles move the head with respect
to the torso. The torso, in the case of the pigeon above, may also be moving
(if locomoting forward, we are in the topic of optic flow--see notes
at bottom of Direc Selec page)
VOR saturates if head rotates more than 60 deg/sec...
During running angular head velocity does not exceed 100°/sec
most energy of head rotation in the 0.5 - 5.0 Hz.
"What mechanisms operate to hold the head as a relatively stable platform
during locomotion? Four main factors have been studied in humans:
(1) mechanical forces due to the inertial mass of the head and the muscles and
tissues that support it.
(2) the vestibulocollic reflex by which vestibular inputs activate neck muscles
to stabilize the head w.r.t. space.
(3) the cervicocollic reflex (CCR): the stretch refex
of the neck muscles, which acts to stabilize the position w.r.t. the
trunk.
(4) voluntary control of the neck muscles."
Stretch reflex: stretching of a muscle causes
negative feedback to its motoneuron, to reduce contraction. Does CCR act to
prevent oscillations of the head? "To stop the head from oscillating, the
VCR and the CCR may adjust the ratio of the viscosity to elasticity of the neck
muscles and connective tissues."
PPRF: paramedian pontine reticular formation
"Two classes of burst neurons in the PPRF of alert monkeys have been defined:
those with discharge activity related to the size of he eye-in-orbit movement
(ocular burst neurons) and others that discharge in relation to the size of
the eye-in-space movment (gaze burst neurons)."
Eye-head saccades:
Appreciate that it is possible to see a target at the limit of your periphery,
but not be able to foveate with a saccade alone. Thus a horizontal head rotation
is made too. {sidebar on intraocular pressure, glaucoma
and peripheral vision) See figure below.
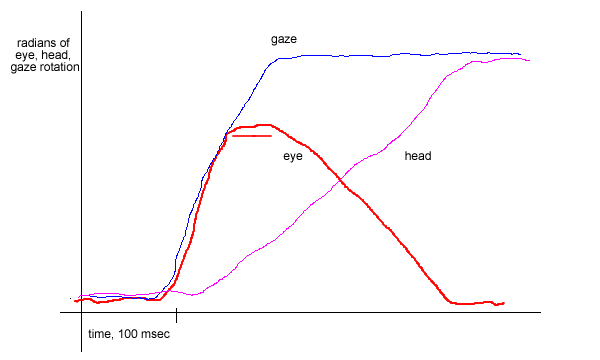
One paradigm: At t=0 there is motion (say 30 deg/sec) of a small foveated target
toward the periphery; the target will keep moving until it stops somewhere beyond
the eye movement say (say 90 degrees). After a delay SP starts and will be aided
by a small corrective saccade. The eyes can keep tracking the target until it
approaches the limit of foveated eye position. About then the head starts moving
in the same direction as the eyes. Until the gaze reaches the target, the
eyes stays fixed to a peripheral angle--during which time VOR must be suppressed.
When gaze (= head + eye) places the target on the fovea (of the one eye
that can see the target...) VOR is "uninhibited" and continues until
the head faces the target.
Movement to a target that appears away from foveal fixation. See L & Z
Fig 7-2. unexpected vs predictable responses.
The saccade, with a latency of 200 msec, precedes the head rotation by about
50 msec.
SP and head movements:
See L&Z3 Fig 7-4, patient with loss of vestibular function, compared to
normal. The head brake experiment: have the head rotate at same velocity as
target, so no eye movement is required. Suddenly the head stops. In a normal
subject the tracking continues smoothly, thx to SP operating "in the background".
In the impaired subject catch-up saccades and too-slow SP ensue.
Model of head
rotational inertia of the head:
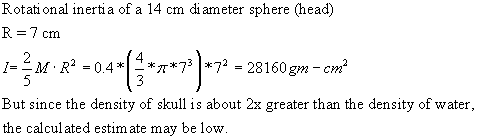
In fact the website
http://alexandria.tue.nl/extra2/200611939.pdf
cites a gm-cm^2 rotational inertial of a human head about the z-axis of 150,000.
Let's compromise and say 100,000.
Estimating K, the stiffness: How much deflection, in radians, would result
from 1lb = 454 gm held in the mouth?
My guess: 0.1 rad. So torsional stiffness K is estimated to be
454gm * 980 cm/s^2 * 7 cm radius / 0.1 rad = 31,144,400 dyne-cm/radian = 31
x 10^6
Let's say the time constant Tau of head rotation is 450 msec, 3x greater than
the eyeball in its orbit.
How is K related to Tau? Tau = B/K, so B = K*Tau = 14x 10^6 ; What are
the units?
Let's use the following transfer function to model the mechanical load of the
head:
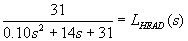
where we have scaled the terms above by 10^6.
Is the head overdamped or underdamped?
More realistic: What to do about the torsional spring? Why does the head
stop rotation where it does?