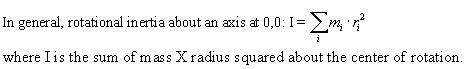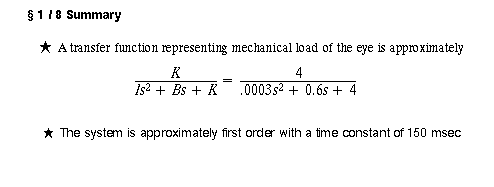The load for an extraocular
muscle is the eyeball in its orbit.
1. The eyeball itself has rotational inertia I. (mR^2 term).
2. A contracting muscle (for example the medial rectus) works against the spring
force of the passive antagonist muscle, the lateral rectus.
3. And as the eye moves in its socket it experiences a drag force, due to the viscosity
of the lubricant and connective tissue between the orbit and the socket.
The eye is rotated by contraction of a muscle or muscles, and the muscle is in turn
controlled by pulses (spikes/sec) from motoneurons in the brainstem.
In the development below we assume the radius of the eye is 1.25 cm.
Reading:
¶Chapter 7 of RHSC2, pp 165-181. What is considered by Carpenter becomes
a more complicated model than we need for the purposes of EN122. We will concentrate
on a second order linear systeml that accounts for rotational inertia, stiffness
in the torsional spring sense, and drag due to rotation of the globe in the socket.
Note at the top of p. 172
RHSC defines "gram force"
gf = 9.81 x 10-3 N = 981cm/s2 x 10-3kg x 10-2m/cm,
which is 981 dynes and is the force (not torque) of a 1 gram weight (see below).
RHSC uses the gf in subsequent graphs
To help with our calculations,
we will look ahead and borrow some results from chapter 8, pages 200-207 that describe
the pulse patterns of oculomotor neurons which control the eye muscles.
Calculating moment of inertia
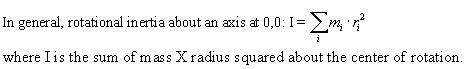
Look up the formula for rotational inertia of a sphere and assume an eyeball radius
of 1.25 cm, then
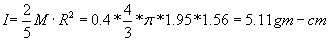
Chpt 7 RHSC2 points out that the fluid in the eyeball may lag behind in rapid rotations,
somewhat reducing the effective rotational inertia.
Measuring the stiffness of the antagonist muscle
Remember F = K*Δx, Hook's Law for a linear elastic spring?
For rotation of the eye we want a stiffness K such that torque T = K*Δθ.
Robinson (1964) glued thin surgical thread to a contact lens on
the cornea and ran the thread over a pulley to a weight.
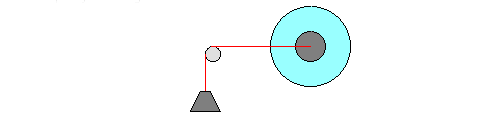
Robinson found that 1 gm of mass on the thread deviated the eye by 1 degree.
RHSC pp 172-173 show muscle length tension plots. In particular, Fig 7.33(b) shows the natural condition angle-tension slope for human lateral rectus. From this data and others RHSC says on p. 174 "...estimates of the passive stiffness have ranged from 0.5 to 1.5 gf/deg..." We can settle on 1 gf = 980 dynes force, and consider the radius for torque to be 1.25 cm.
Working in the CGS system, with g = 980 cm/sec2, we have
K = Torque/Δθ = 1 gm * 980 cm/s^2 * 1.25 cm radius / (1/57 deg/radian)
= 69825 dyne cm/radian;
the torsional spring constant.
¶
¶
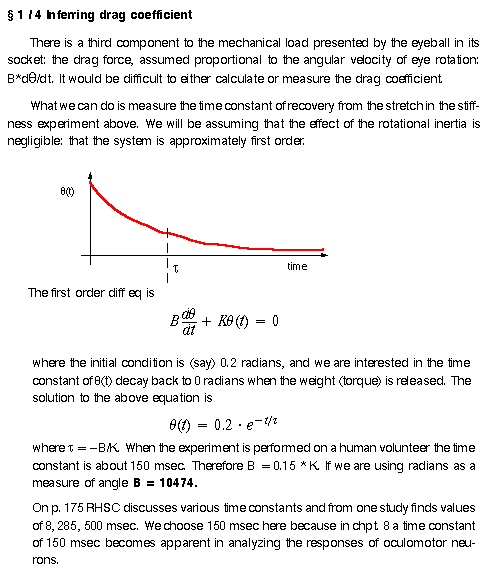
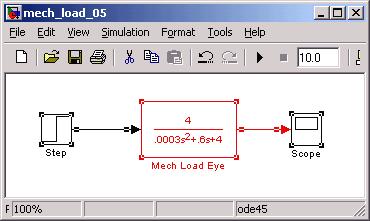
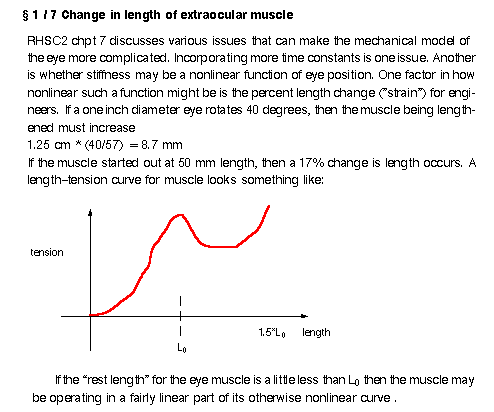
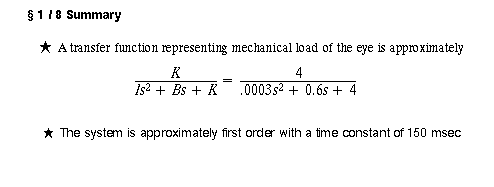