Two antagonistic springs of equal length and different stiffness balanced by shortening the less stiff spring.

Recall that stiffness K of a linear spring is defined by Hooke's Law:

where σ is stress (Force/Area) and ε is strain (delL/L0).

Imagine a spring of rest length L and stiffness K. What will be the stiffness of two such springs hung in series? Answer: K/2.

See derivation of the effective stiffness of two springs in series at this Wolfram site.

In general, the series stiffness of two springs with individual stiffnesses KL and KR is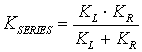

By induction, 4 springs of stiffness K in series will have K/4 stiffness.

Now imagine two springs on either side of a globe fixed in a socket so it can't be pulled backward...it can only rotate about its vertical axis. The rest length of each spring is 4cm but their attachments to the globe pull them to about 5cm length. The left spring has more stiffness than the right one.

Because the left spring is stiffer, the globe is looking to the left (let's say by 11.4 deg = 0.2 radians).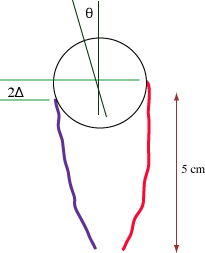

What is the difference in stiffness that creates such a rotation? See above that the left spring is Δ shorter than 5cm and the right spring is Δ longer.

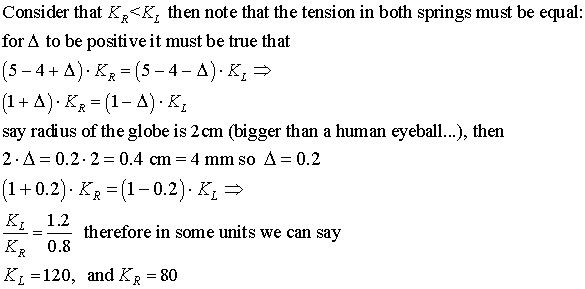
Note above the definition of 2* Δ as the arc length of the 11.4 deg turn.
You should be able to derive the same answer/ratio by minimizing energy:

Now suppose we want to straighten out the globe (make it "look" directly ahead) by shortening the weaker spring on the right. Exactly how much should we shorten it by? Keep in mind that by shortening the right spring we increase its stiffness...

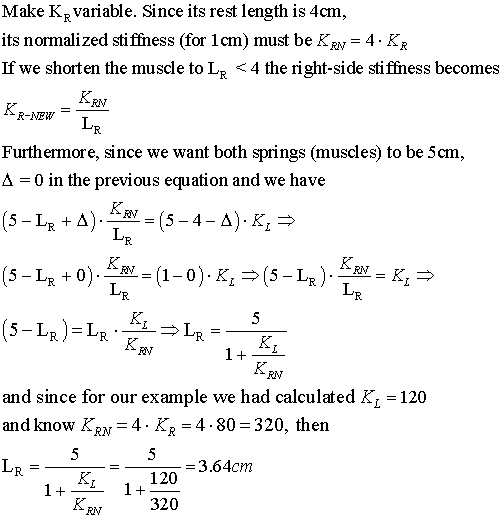
so the right muscle/spring needs to be shortened by 1.36 cm, attached to this (large) 4cm diam globe.

Do the math to check the result:
effective stiffness of the shortened muscle is K_R=320/3.64=88; |
and (5-3.64)*88 = 120, which is tension (5-4)*120 on the left side.