
----------------

Terminology: By "muscle" we mean whole muscle,
such as the gastrocnemius or biceps or deltoid muscle.*

Whole muscle is made of many muscle fibers in parallel. One fiber may be as long as the whole muscle, but only about 10 microns in diameter. We will discuss the orientation of muscle fibers in whole muscle-pennate muscle has diagonally oriented fibers to increase strength at the expense of maximum length change. A muscle fiber is a muscle cell. During development many myoblasts coalesce into one fiber, resulting in one cell with many nuclei.
Does muscle change volume during contraction? No!
Supplemental Reading
Excerpts from chpt 1 of T. A. McMahon, Muscles Reflexes and Locomotion.
Princeton Univ. Press (1984).
NOTE. Tom McMahon, a biomechanics professor at Harvard, died in early 1999, at age 55.
Mechanical use of muscle
Passive muscle has the length-tension properties of a non-linear spring. Active
muscle contracts. And when it does so it may reduce the angle of a joint, or force
blood out of the heart, or rotate the eyes, or generate speech. In the skeletal
system muscle is fundamentally a torque or moment generator.
![]()
If the load muscle pulls against is at an equilibrium torque value T0, muscle (+tendon)
won't contract, but will develop tension (isometric). How long active muscle can
maintain tension depends on how well supplied with energy it is; muscle which develops
tension most quickly is the type of muscle most likely to fatigue during sustained
activity.
Here we focus on the properties-material, biochemical and mechanical-of muscles, and consider the use of muscle to rotate limbs in vertebrates.
Muscle joins to bone by series connection of tendon. Tendons are passive collagenous tissues which cannot contract. It will turn out that many experiments which demonstrate muscle properties utilize muscle disconnected from any bones: they're simply held by tendon and the tendon is connected to a force gauge.
History. I imagine cavemen scrutinized muscle when they cooked it over fire. Heat-treatment of muscle in rigor mortis further stiffens the tissue by cross-linking proteins. Scientific study of muscle probably began with the Greeks, and Aristotle. See Martha Nussbaum's translation of Aristotle's De Moto Animalium [On The Motion of Animals]. Aristotle made the analogy that animals moving were like puppets, controlled by "strings" from what centuries later would be known as nerve fibers of the central nervous system.
To understand the role of muscle in movement, you must start with stress-strain relationships. In EN41 you learned that the stress-strain curve is a fundamental descriptor of a material. Here we consider the stress strain curves of unstimulated and stimulated muscle. Unlike most of the uniform materials of EN41, muscle is a relatively complex tissue and different component may contribute in different ways to the stress-strain curve. Recall the units of stress and strain!
Passive muscle
Passive muscle has a non-linear stress-strain curve. The first equation in TAM,
on page 8, says that the rate of stress change as a function of strain change in
unstimulated muscle is proportional to stress.
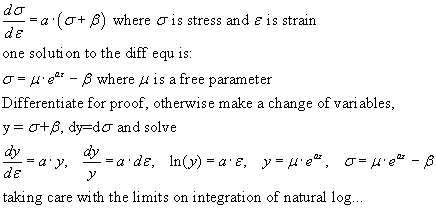
Remember that strain is a dimensionless quantity of Δlength/length, So a must be a dimensionless constant.
McMahon makes an analogy between stress-strain in passive muscle and stress-strain in yarn. Pull slowly on loose yarn. As more strands of yarn are brought into tension, the yarn resists increased pull in the non-linear way suggested by the equation above. In the reading of TAM chpt 1, see Fig. 1.6. The bottom curve is for passive muscle. Below rest length L0 muscle offers no resistance to being stretched, much like loose yarn doesn't resist until at least a few strands are pulled to their full length. Passive stress continues out to 1.5 * L0.
Stress-strain curve of active muscle
The upper curve in TAM Fig. 1.6 shows stress-strain for active
muscle. Notice stress now starts at 0.5 l0. The curve is a combination of active
and passive effects. If the passive curve of Fig 1.6 is subtracted from the stimulated
curve, then a bell-shaped curve in Fig. 1.7, labelled "Developed" by TAM,
results. Note that the maximum tension of active muscle is not at the greatest length.
TAM explains the bell shape of the active curve later, in his chapter 3. See Fig.
3.7. At the sarcomere length where all myosin fibers can make contact with actin,
muscle exerts maximum tension. Otherwise muscle is on one side or the other of the
bell curve which represents a lack of actin-myosin crossbridge coupling. We discuss
below the crossbridge cycling mechanism which accounts for the increase in stress
of active muscle.
Muscle in situ, in a living mammal, is rarely stretched more than 10%.
See TAM fig 3.7 for "molecular" explanation of length-tension curve
read about rubber elasticity in Wainwright et al. 1976,
Mechanical Design in Organisms, Halstead Press, page 54. QP303/M4.
Actin and myosin
Actin and myosin are filamentous proteins which interlock and overlap in a way to
produce length change and tension development in skeletal muscle. First we discuss
the arrangement of myosin and actin in muscle sarcomeres. In the schematic
below approximate relationship between thick myosin and thin actin fibers is illustrated.
Not shown is the inhibitory tropomyosin molecule. Histological labels are shown
in capital letters. The A label marks the myosin position, not the actin!
The M line marks the midpoint of the myosin fibers, the Z line
marks the midpoint of the actin fibers. H is the distance between the ends
of actin filaments.
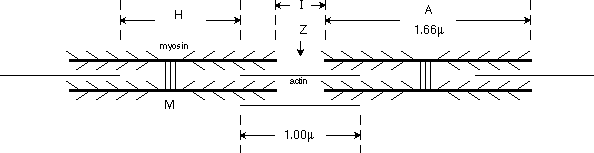
End-on, myosin and actin form overlapping hex and triangular arrays, as shown below.
The ratio of thin to thick filaments is 2:1
Myosin filaments are about 1.66m in length; actin filaments are about 1.0m
Bundles of myosin and actin group together in myofibrils, and the fibrils group
into muscle fibers. A fiber is one (multi-nucleated) muscle cell.
The structure of myosin is now known in great detail, amino acid by amino acid. In 1993 Science magazine (24th December issue) selected myosin as 1st runner-up for Molecule of the Year. The complete 3-D crystal structure of myosin, to a resolution of 2.8 �, was published, and specific locations where the myosin head could flex and where ATP could bind were suggested. A similar structure for actin was published in 1992.
TAM chapters 3-5 go into detail about the mechanism of crossbridge attachment and
force development in muscle fibers. Here we outline what is known.
EVENTS BEFORE CROSSBRIDGE CYCLING.
Before actin-myosin crossbridge cycling can occur tropomyosin must be moved out of
the way. Troponin is a component of tropomyosin; it blocks myosin from its binding site.
Tropomyosin is inhibited (moved) by calcium, which is released from sacroplasmic
reticulum in muscle. Sarcoplasmic reticulum is induced to release calcium ions when a
voltage reversal occurs at the muscle cell membrane. Neurotransmitter (acetylcholine,
ACh) from a motoneuron axon interacts with a receptor at the neuromuscular synapse to
open sodium channels which lead to the transient membrane voltage reversal. And all that
happens BEFORE crossbridges can cycle! To put the events in the form of a "program:"
1. Pulse travels down motoneuron axon to neuromuscular synapse.
2. Depolarization of pulse at presynaptic terminal causes packets of ACh to be released.
3. ACh diffuses across 10 angstrom synaptic gap to cause conformation change in
postsynaptic receptor protein.
4. Channels in receptors open and allow Na+ ions to flow in the muscle cell.
5. Inward sodium current depolarizes muscle cell from negative potential.
6. Depolarized state causes sacroplasmic reticulum to release calcium in muscle cell.
7. Elevated Ca++ level in muscle cell forces tropomyosin to change conformation and pull
away from actin and myosin. It is a physical movement of tropomysin, away from the
binding site.
As long as tropomyosin is out of the way actin and myosin can interact.
SEQUENCE OF EVENTS WHICH OCCUR DURING CROSSBRIDGE CYCLING:
1. The head of a myosin molecule binds to actin. There is ADP still on the myosin from a
previous cycle, and this ADP is now released, resulting in...
2. Myosin heads flex in tandem, pulling the actin strand 50-100 angstroms into the
myosin channel and contracting the muscle. If the load on the muscle is too great, no
movement occurs, but tension develops. The myosin head flex is an example of protein
conformation change. The energy required to flex the myosin head has been previously
stored in the myosin molecule and is now expended.
3. The conformation change in myosin exposes a site where ATP can bind.
If ATP is present it binds on the flexed myosin. Binding causes release of
myosin from actin.
4. The myosin head releases from the actin; Hydrolysis of ATP to
ADP causes the myosin to cock back. The split of ATP (into ADP + phosphate)
stores energy in the myosin head and releases some heat. Phosphate leaves the reaction
site.
5. The cycle starts again if the myosin head finds a new actin binding site.

If ATP is not present and tropomyosin is inhibited, the myosin stays bound to actin. If ATP never returns, then a state of rigor mortis ensues. If the load is such that actin doesn't move with respect to myosin, the myosin stays linked to the actin for a longer time. The ATP doesn't have a chance to latch onto the myosin and release its energy and heat. As a consequence, isometric muscle releases less heat than contracting muscle. If the load is so great that muscle is stretched during crossbridge cycling, then crossbridges are prematurely torn apart and micro-injury occurs in the muscle. The micro-injury is a stimulus for muscle to "repair" itself into a strengthened state. (Thus muscle-building during weight-lifting occurs only during the "negatives." A negative occurs when the weight is slowly lowered by the lifter. As you lower yourself during a push-up, you do a negative. So too with slow release from a chin-up.)
Nature 352 (25 July, 1991): pages 284
& 352, "Biomechanics goes quantum,"
the power stroke is 10 nm; the myosin head is about 20 nm long.
The more overlap of myosin and actin during crossbridge cycling,
the greater the tension in the muscle. Why? more myosin heads can make contact with
actin! At rest length l0 actin and myosin overlap to a maximum degree, thus the
peak in the active length-tension curve seen in TAM Fig. 1.7.
Overall muscle strength depends on length of the muscle. Try sensing strength of grip with various wrist angles. At what wrist angle is grip strongest? Why?
Recovery of ATP
See chapter 2 of TAM, on thermodynamics of contration.
And New Scientist 13 Jan 1996 article.
Linearizing L-T curve with antagonist
Tie two muscles together end to end and between two fixed points, so that both
muscles are relaxed and at length L0. Now stimulate one muscle and leave the other
relaxed. The stimulated muscle will contract and the relaxed one will lengthen to
the total length constant at 2*L0. Your question: what will be the stimulus tension
curve for the overall system? imagine a tension meter reading off the in-series
tension of the pair. The answer to this question will tell you something about muscle
agonist-antagonist pairs.
As you will learn later, it is easier to make a control system
for muscle if muscle has linear elasticity (constant k in F=k�Δx) instead
of the non-linear curve we see here. Most skeletal (and extraocular) muscles have
antagonists: biceps vs triceps etc, in the skeletal system it's usually a flexor
vs an extensor muscle. If we plot L-T for each muscle on the same graph paper and
take account of the different directions agonist and antagonist are stretched,
we see something like this:
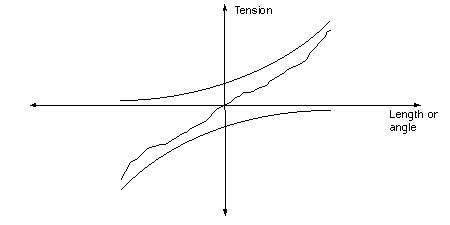
The top curve is the standard L-T curve; the antagonist curve below shows the effect of the
antagonist resisting the agonist along the force direction used for the agonist. For example,
at L=0 or L0 both are pulling equally against each other and there is no net force on the
load. The overall effect of the antagonist is the linearize the combine length-tension curve.
If l is the length variable and M(l) is the LT curve of one muscle, then the combined curve is
CT = M(l) - M(-l) or �Odd(M(l), where Odd finds the odd part of M(l), and
ODD(x) = -ODD(-x).

Hill's equation
Years before the protein constituents of muscle were known, experiments were
done on the mechanical properties of isolated whole muscle. On page 10 of TAM, dynamic
("quick-release") experiments on isolated muscle described. A muscle is
stretched to a constant length while stimulated to tetanus, then it is released
against a variable load. Below are shown a series of quick release length changes
as suggested by the single graph of TAM's
fig. 1.8(b). The length Δx1 decreases more in the top graph because the
muscle has the opportunity to contract against the light load. As TAM asks, pay
particular attention to the (negative) slope of the length change at time of release;
that's the velocity of shortening, v.
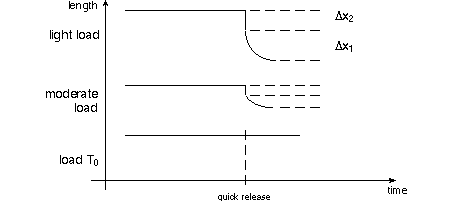
A series of quick release experiments will show an inverse relationship between
load and velocity of shortening.
See
EN123 Lab VT for notes on Hill's equation. Hill fitted the data empirically
to his equation
"Built for jumping: The design of the frog muscular system," G.J. Lutz
& Lawrence C. Rowe, Science 263: 370-72 (Jan 24, 1994). Good
SL-force curves, and power vs velocity curves. No mention of Hill's equation!
In the Lutz & Rowe report they used film to determine peak
power by measuring change in the center of mass. They found 67.2 Watts/kg of body
mass. 1 W = 1 J/sec. In tests on the muscle they found it generated 371 W/kg. By
dissection they found that the muscle involved in jumping accounted for 17% of the
animal's weight. 17% of 371 = 63 Watts, a good approximation.
Force
Length and Force are the two important ways of describing the states of muscle.
Negative velocity muscle: the only way to build muscle.
Mechanical model for muscle
The quick release experiments lead first to Hill's equation, and second to a mechanical
model for muscle and tendon. The diagram below illustrates the components. The series
spring is tendon. The parallel spring is the non-contractile and connective tissue
in muscle itself. The contractile element has two parts: the sites of active tension
(actin and myosin fibers) and a dashpot which resists stretching with a force proportional
the rate of change of dimension x. The dashpot represents viscous elements in muscle.
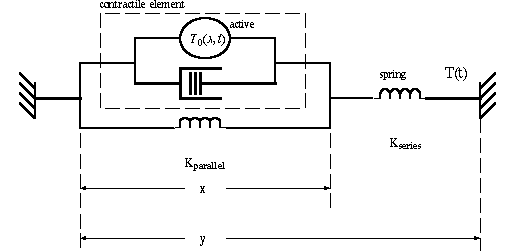
The mechanical model results in a differential equation description of muscle length
change y(t). Start with the contractile element, then put its expression for x in
parallel with the inner spring, then that whole expression in series with the outer
spring. [See end-of-� problem]. Say the outer spring represents the tendon in series.
Let it be an isometric contraction with constant length Y0. Solve for x(t) as a
function of neural input T0(x,t). The three elements in parallel must have a tension
which is equal to the series tension,
![]()
Isolate the x-dot term and you're ready for MATLAB.
Use MATLAB or SIMULINK, and plot the result. On MATLAB try
[t,x] = ode23 ('tam22', t0, tf, x0);
where tam22 is a function you write which describes the first derivative. (TAM page
22, a model which neglects the Kparallel)
t0 & tf are the starting and stopping times for the simulation and x0 is the
initial condition. Suppress intermediate printing with semicolons. After ode is
finished, plot with
plot (t, x)
Read more in the MATLAB documentation on the balcony. Or just type help plot or
help ode23 while in MATLAB.
In the M-file tam22.m can be the lines
function tdot = tam22(t,ten)
B = 10;
K = 4;
T0 = 0;
if ( rem(t,12) < 6) T0 = 4; end
tdot = (K/B)*(T0 - ten);
MATLAB has a built-in editor for writing the M-file function.
On the command line you can type
t0 = 0; tf = 20; x0 = 0.5;
[t,ten] = ode23('tam22', t0, tf, x0);
plot (t, ten)
and you will see the plotted result in a figure, similar to the TAM page 23 results.
Muscle mechanics around joints
Why is muscle so long? Why isn't muscle short and stubby, near the joint (b)?
On the other hand, why is muscle so short? Why not be longer, and stretch from one
end to the other? (c) What mechanical advantage (or dis-advantage) occurs for the
way muscle acts to rotate bones at joints? Keep in mind that muscle has a limited
range of contraction, compared to the large amount of movement required at the ends
of the limbs.
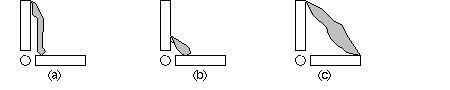
The situation in (a) means that a long muscle has a chance for a significant shortening
l�l, whereas (b) is too short to create much rotation. The great leverage of (c)
is impossible unless a pulley re-directs force, or the muscle extends across webbing.
Types of striated muscle
So far we have been assuming that striated muscle is of one kind. Yes, all striated
muscles use the same actin-myosin ratcheting mechanism for contraction and development
of tension, but in fact there are two major types of striated muscle fiber. The
distinction is greatest in non-mammalian vertebrates, where the fibers are called
FAST and SLOW. On a fiber-by-fiber basis FAST and SLOW compare in the following
ways:
| FAST | SLOW |
| large maximum tension | small maximum tension |
| short delay from stimulus to tension | longer delay |
| easily fatigued | greater endurance |
| pale appearance | the "dark meat" (blood supply) |
| anaerobic metabolism | aerobic |
In mammals the distinction is between fast and slow twitch muscle, which are more properly called FG, for fast-glycolytic and SO for slow-oxidative. It is known that muscle fibers remain segregated in regard to which motoneurons innervate them. By virtue of their performance as strong, easily fatigued fibers the FG fibers are used for jumping, kicking and other movements which are intense and brief (predator, like swordfish, going after prey...). On the other hand SO fibers may be involved in posture and sustained activity such migratory bird flight, where endurance is at a premium.
Muscle fatigue, strengthening and injury
Muscle changes. Over the short term it contracts and warms up. If exercised too
much, it can fatigue. Certainly white fast-twitch muscle can fatigue biochemically
after a dozen twitches because ATP is depleted. Another kind of "fatigue"
results from the micro-injury of active muscle that is lengthened; this kind of
fatigue results, over a day or so, in strengthening. Just what is the biochemical
stimulus for strengthening due to the micro-injury of "negatives"? It's
not clear to researchers. See Chpt 2 of TAM for some thoughts. It is known that
increase in muscle bulk comes from a thickening of existing fibers, instead of growth
of new fibers.
If muscle is not used, it atrophies. If muscle is in weightlessness, it atrophies a lot! Unused muscle around bone which has healed from a fracture is smaller than the muscle around active bone. Soviet cosmonauts learned the hard way about the atrophy of disuse; they were unable to walk away from their space vehicle when it returned to earth after months of weightless orbit! American astronauts exercise on treadmills in the Space Shuttle while it is in orbit, to minimize the atrophy of muscle not required to resist gravity.
As far as I know, tendon and ligament cannot be strengthened by use or weakened by disuse. Bone? I think studies have shown that limb bone unused for long periods of time loses some of it capacity to "remodel" after stress. I'd like to know more!
A muscle is thickest in its middle, thinning as it approaches the tendons. Since, for a muscle in static equilibrium, the tension is uniform along its length, the thin sections of muscle bear the greatest stress. The points of contact with tendon are therefore the most likely places for injury. You'd think Nature would have made the injury threshold of muscle greater than it is possible for an animal to exert, so self-inflicted injury could not occur. However, it is sometimes possible to tear or "pull" muscle by exerting too much if the muscle has not been "warmed up." Some muscles, such as the hamstring, are especially susceptible. If I dive cold into the pool and start a strenuous breast-stroke frog kick immediately, I can pull a hamstring.
Muscle injuries most often occur when an external force [often from the ground] causes an un-natural pull. Muscles, however, are not the weakest links in the musculo-skeletal system. As sports medicine specialists will testify, ligaments tear before muscles pull. Thin tendons are generally more susceptible than muscle itself, too.
Muscle can have problems other than fatigue. Cramps occur when an errant hormonal or neural signal causes all the fibers in a muscle to contract at once. An epileptic seizure starting in the cortex can send synchronous excitation down through the motor system, contracting muscles simultaneously.
Summary
* Passive stress-strain curve of muscle is non-linear, like yarn being pulled apart.
* Active stress-strain curve depends on actin-myosin overlap.
* Agonist-antagonist (flexor-extensor) muscle pairs have a more linear stress strain
curve which can be characterized by on modulus of elasticity.
* The energy for flexing myosin head wrt to actin comes from the splitting of ATP
during detachment of myosin, and its subsequent extension for another cycle. The
splitting of ATP release heat.
* Quick release experiments lead to Hill's equation relating force and velocity.
* There are two types of mammalian muscle fibers: FG and SO. FG are fast, strong
and easily fatigued. SO are slower, weaker, and more enduring.
* Lengthening active muscle results in torn crossbridges which result, over a day
or so, in strengthened muscle.
* Injuries to the musculo-skeletal system often occur at ligament, tendon and bone,
before injury to muscle.
* Cardiac muscle is striated and has the same shape L-T curve as skeletal muscle.
It is stimulated by electrical contact with other muscle cells, not by axons from
motoneurons.