EN224: Linear Elasticity            

          Division of Engineering

1.3 Constitutive Law for Linear Elastic Solids

As before, we will begin by reviewing constitutive models for large deformations.
We will define an elastic solid from thermodynamic considerations.
We make two key assumptions regarding the behavior of the solid:

ASSUMPTION 1: Local Action

Stress at a point X depends only on the deformation of the immediate neighborhood of X.

Implication: we need only specify the response of the solid to homogeneous deformation (recall that all smooth deformations are locally homogeneous).

 

ASSUMPTION 2: Equation of State

State is completely characterized by Lagrangean strain E and temperature q

Hence, there exists a specific internal energy u(E,s), where s is the specific entropy.
Measuring u(E,s) and s(E,q) would completely characterize the material.

Given u(E,s) and s(E,q), we may define the Helmholz free energy

Given u or F, we can find the stress-strain-temperature response of the solid:

I: Isothermal deformations

Consider quasi-static state change

Then

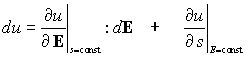
Now, recall the first law of thermodynamics

Where dw is the work done on the solid per unit reference volume, and dq is the heat flow into the solid per unit reference volume.

From the power identity and the second law:

Where is the second Piola-Kirchhoff stress.

Hence, comparing the two expressions for du shows that

II: Isentropic deformations

Consider a quasi-static state change

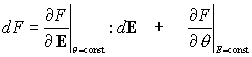
Now,

So

Hence

Thus, we have two alternative expressions for the stress. We will write

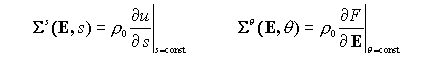
Linearized constitutive law

We proceed to linearize the general stress-strain response. To this end, we suppose that E is small in some sense (we only know what `small’ means if we know the form of the expressions for ). In addition, assume that the reference configuration is stress free (it is trivial to generalize to stressed reference configurations).

Then, expand the expressions for to first order in E

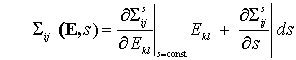
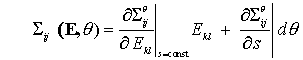
To simplify, we introduce the elastic constants

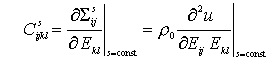Adiabatic elastic constants

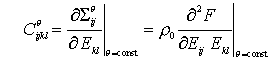Isothermal elastic constants

.Similarly, define

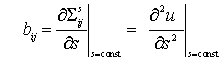
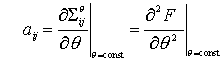
It is worth noting for future reference that u and F are positive definite.

Voigt Symmetries

Our two assumptions impose three restrictions on the elastic constants

1. (since )

2.(since )

3. (because of 1. and 2.)

Thus, has 21 independent constants.

Linear Elastic stress-strain-temperature relations

We now introduce the approximations discussed in 1.1; 1.2.

Let

Then

We could invert these expression. Let

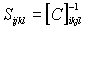
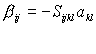
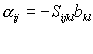
Then

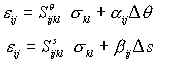
Some terms: are the components of the elasticity tensor
are the components of the compliance tensor

are the components of the thermal expansion coefficient

Observations

For (a) Isothermal or (b) Adiabatic, isentropic processes

(a) (b)

A solid with this constitutive law is called a Linear Simple Solid.

Note that we could measure the elastic constants under either isothermal or adiabatic conditions. The two tests do not give the same values. However, the difference is very small and we usually do not distinguish between and . We will drop the distinction from now on.

Note that the symmetries of C allow us to write an expression relating stress directly to displacements:

The second term on the RHS vanishes (can you show this?), and

So

Strain Energy Density

The structure of the constitutive relations outlined above has an important consequence. One may readily show that for a linear simple solid, there exists a scalar potential f such that

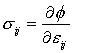
 This holds if and only if , in which case f is given by

The proof is left as an exercise.

Elastic Symmetries

A general anisotropic solid has 21 independent elastic constants.
Note that in general, tensile stress may induce shear strain, and shear stress may cause extension.
If a material has a symmetry plane, then applying stress normal or parallel to this plane induces only extension in direction normal and parallel to the plane

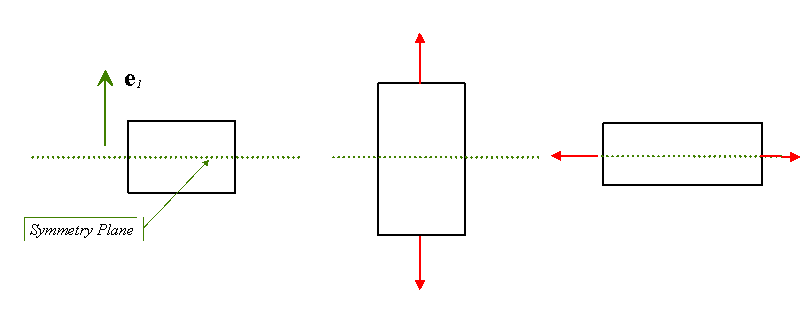
For example, suppose the material contains a single symmetry plane, and let be normal to this plane.

Then

(symmetrical terms also vanish, of course).

This leaves 13 independent constants

Orthotropic material

An orthotropic material has three mutually perpendicular symmetry planes:

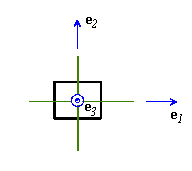
This type of material has 9 independent material constants. Choose basis vectors perpendicular to each symmetry plane, then:

(no sum on i or j)

Isotropic Material

The response of an isotropic solid is independent of the orientation of the loading axes wrt the material.

For this case, C must be an isotropic tensor.

From the representation theorem for isotropic tensors (see Atkin and Fox, 1980) C must have the form

Where l, m and g are constants.

To satisfy , we must have m = g.

Hence,

or

This expression may be inverted (contract i and j, solve for and substitute back)

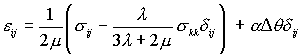
 Where the last term is the strain due to thermal expansion.

l and m are known as the Lame constants.

Several other forms of this constitutive relation are often used:

Here, E and n are Young’s Modulus and Poisson’s ratio, respectively, while K is the bulk modulus.

Relations between the constants are tabulated below

Restrictions on Values of Elastic Constants

Recall that thermodynamic considerations require that for all .

We will show that, or

Begin by expressing in terms of the stress invariants. Note that

Recall that the invariants of are

Hence

Observe that since may be expressed in terms of the stress invariants, it is independent of our choice of basis. Hence, we could just as well express in terms of the principal stresses. It is straightforward to show that

Finally, to prove our assertion, consider particular stress states.

Let                      

To prove the converse, write

Whereupon it is clear that for nonzero states of stress