EN224: Linear Elasticity             

      Division of Engineering

1. Review of the Field Equations of Linear Elasticity

Objective: derive field equations governing the behavior of linear elastic solids from the perspective of finite deformations of general solids.

Review constitutive models for elastic solids

1.1 Kinematics of Deformable Solids

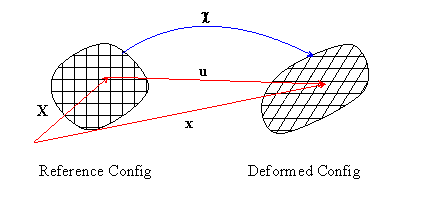
We describe the deformation and motion of a solid by a mapping.
Suppose a material is at position X in the undeformed solid, and moves to a position x
when the solid is loaded. A mapping

would describe the motion.

We assume that c is twice jointly differentiable wrt time and position, and satisfies

The displacement of a material point is

Homogeneous deformations

Homogeneous deformations are of particular interest to us, because the constitutive response of a solid is usually determined by measuring the forces required to induce a homogeneous deformation within a solid specimen.
A homogeneous deformation has the form

Where A is a constant two tensor such that det(A)>0, and c is a constant vector.

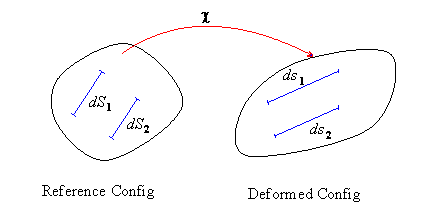
Imagine drawing two straight, parallel lines on the reference configuration of a solid.

If the deformation of the solid is homogeneous, the two lines remain straight in the deformed configuration, and the lines remain parallel. Furthermore, the lines stretch by the same amount, i.e.

Every (smooth) deformation is locally homogeneous. To visualize this statement, imagine drawing a straight line on the reference configuration of a solid. The line would look like a smooth curve on the deformed configuration. However, suppose we focus attention on a line segment much shorter than the radius of curvature of this curve. Our segment would be straight in the reference configuration, and would also be (almost) straight in the deformed configuration. Thus, no matter how complex a deformation we impose on a solid, infinitesimal line segments are merely stretched and rotated by a deformation.

To specify the constitutive response of an elastic solid, we need a measure of the deformation in the immediate neighborhood of a point in the solid. For example, we could track the deformation of a segment dX at point X in the ref. config:

where F is the deformation gradient at X.

Actually, it is better to find a measure of the change in length of dX rather than to find its image in the reference configuration. For this purpose, note that

provides a measure of the length change.

We therefore use the Lagrangean strain tensor E to characterize the deformation near a point.

Infinitesimal Deformations

 

We need to make a number of assumptions to simplify the equations of linear elasticity. One is to assume that deformations are infinitesimal. In most practical circumstances it is sufficient to assumewith

Note that and so

We use the latter, linear measure of deformation in linear elasticity, and define the infinitesimal strain tensor

In component form

where the comma denotes differentiation with respect to a spatial coordinate, in the usual manner.

 

Some remarks on deformation measures for linear elasticity

Recall that in general finite deformation kinematics, a homogeneous deformation may be decomposed into a sequence of a rotation followed by a stretch, or alternatively into a stretch followed by a rotation (the polar decomposition theorem), i.e.

Where R is a proper orthogonal tensor (representing a rigid body rotation), and U,V are symmetric stretch tensors.

 

There is an analogous decomposition for infinitesimal motions. Note that

plays the role of F. We may write

Here is a skew tensor, which represents an infinitesimal rotation.

 

To see that w represents an infinitesimal rotation, consider a deformation such that

Evidently, this requires that

In other words, the displacement gradient is skew. Let w be the dual vector of w, so that

which we recognize as an infinitesimal rotation.

 

Observe also that the decomposition of is additive. This is unlike finite deformation kinematics, where a sequence of two deformations results in a multiplicative decomposition of the deformation gradient.