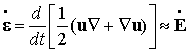EN224: Linear Elasticity       

       Division of Engineering

 

1.2 Kinetics of Deformable Solids

 

We begin by reviewing general measures of force and balance laws.

Internal Forces

 

 

Define   
Note         

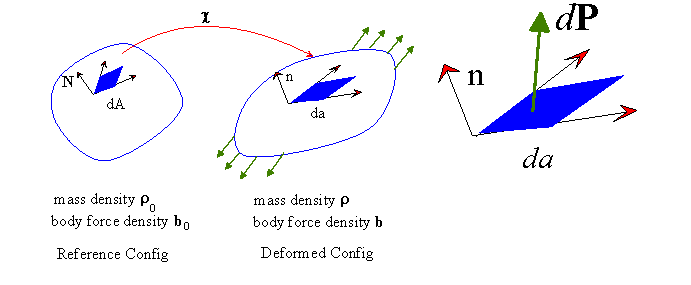
 To characterize internal forces in a solid, we define the Cauchy Stress tensor T such that:

One may define several other measures of stress, for example

First Piola-Kirchhoff stress (nominal stress) S:                     

Second Piola-Kirchhoff stress (material stress) :           

It is straightforward to show that

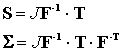
Balance Laws

Let v(x, t) denote the velocity field

 

Linear momentum balance for an arbitrary volume element requires

 

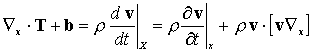
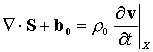
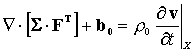
Angular momentum balance for an arbitrary volume element requires

Power Identity

 

Let L = denote the spatial gradient of the velocity field.

The rate of work done on a solid by external forces may be computed as

Remarks: The components of the Cauchy stress tensor are easily interpreted physically: they are the forces per unit area acting on internal planes of the deformed solid. The Piola-Kirchhoff stresses are less easy to interpret. The components of the first Piola-Kirchhoff stress are the forces acting on the deformed configuration, per unit undeformed area. They are thought of as acting on the undeformed solid . The second Piola-Kirchhoff stress has no obvious physical interpretation.

So why do we need to introduce these strange measures of stress? They are perhaps best thought of as generalized forces, in the sense of Lagrangean mechanics. We can choose any set of generalized coordinates we wish in order to characterize the deformation of the solid. Once we choose a set of generalized coordinates, a set of generalized forces follows naturally as the work-conjugate to these coordinates. Evidently, if we choose F as our deformation measure, the appropriate generalized force is the first Piola-Kirchhoff stress S. Alternatively, if we choose E, then we should use as our force system.

 

 

Kinetics for Infinitesimal Motions

We now proceed to linearize the general stress measures and balance laws by assuming infinitesimal motions. Assume

                  

with

Then

Hence

So

We will use to denote stress in linear elasticity.

Balance Laws

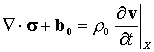
Power Identity