 EN224:
Linear Elasticity
EN224:
Linear Elasticity
Division of Engineering
Brown University
9.2 Solution Anti-Plane Shear problems for anisotropic materials
We focus first on the simple case of anti-plane shear deformation. In this case, there is only one field quantity to be computed, and the stresses and strains are related by the two-dimensional expressions
Only three material constants appear in the constitutive relation. The material is isotropic if . Anisotropy has two effects: applying a shear strain parallel to one axis may induce a component of shear strain parallel to the orthogonal axis (regulated by ). In addition, the shear stiffness parallel to the two coordinate axes may differ.
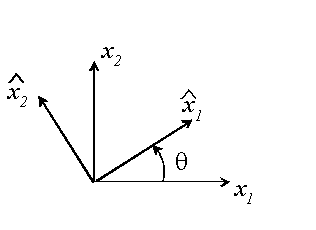
The stiffnesses obviously depend on the choice of coordinate axes. For future reference, it is worth recalling that the material constants transform under an axis rotation as follows
It is always possible to find a particular choice of axes for which . For this special choice, only two material constants appear in the constitutive relation.
Method of solution for anti-plane shear deformations
A simple complex variable formulation can be used to solve anti-plane shear problems. The procedure is very similar to the technique we used for isotropic materials. The procedure is as follows.
Let
![]()
where f(z) is an analytic function.
However, instead of setting ![]() , we now put
, we now put ![]() where p is a complex number given by
where p is a complex number given by
![]()
The stresses can be computed from
![]()
The boundary conditions on f(z) are:
Displacement BVP: ![]()
Traction BVP: 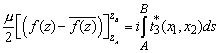
The latter expression can also be used to calculate the resultant force on an arc in a solid, using exactly the same procedure we used for isotropic solids.
Note that the governing equations and boundary conditions are identical to those we obtained for isotropic solids. Consequently, all the techniques we developed to solve problems involving isotropic materials can be applied to anisotropic solids. In addition, many solutions for isotropic solids can immediately be extended to anisotropic materials.
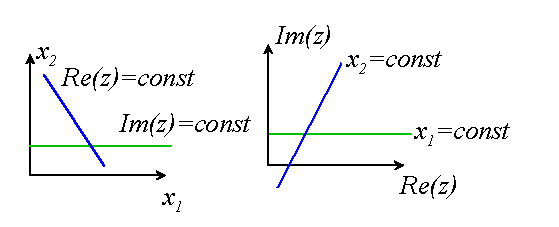
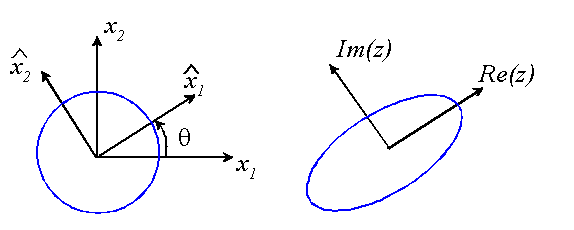
It is helpful to visualize the
mapping from the ![]() plane to the complex
plane, which is illustrated below. If p contains both real and imaginary
parts, the mapping both stretches and shears the solid.
plane to the complex
plane, which is illustrated below. If p contains both real and imaginary
parts, the mapping both stretches and shears the solid.
Note that the transformation is
not a conformal map, since it does not preserve angles. Note also that one can
always define a pair of coordinate axes for which p is purely imaginary. To
see this, note that for the coordinate transformation ![]() shown below
shown below
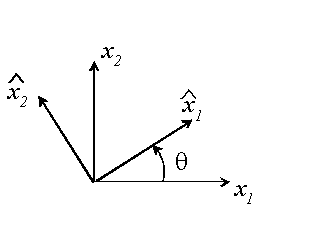
the material constants transform as follows
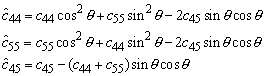
whence ![]() ,
, ![]() ;
; ![]()
Choosing ![]() gives
gives ![]() . For this particular
basis, the mapping simply stretches parallel to the coordinate axes:
. For this particular
basis, the mapping simply stretches parallel to the coordinate axes:
For this special choice of axes,
the mapping has the form ![]() , and the expression for stresses simplifies to
, and the expression for stresses simplifies to
![]()
Proof
The governing equation for the out-of-plane
displacement is ![]()
In addition, the stresses are related to the displacement by
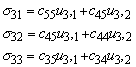
For ![]() , note that
, note that
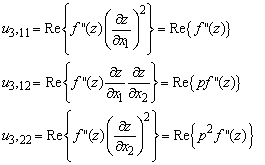
and substitute into the governing equation to see that
![]()
This is satisfied by
![]()
as stated. Note that ![]() is real, and that
is real, and that ![]() for an isotropic
solid, so we recover our original results.
for an isotropic
solid, so we recover our original results.
The stresses can be computed from f(z) as follows. Using the expressions for stress, we have
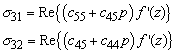
Note that
![]()
giving
![]()
The boundary conditions for a displacement BVP follow trivially. For the traction BVP, note that the boundary condition may be expressed as
![]()
Using ![]() and the expressions
for stress components above, this may be rewritten as
and the expressions
for stress components above, this may be rewritten as
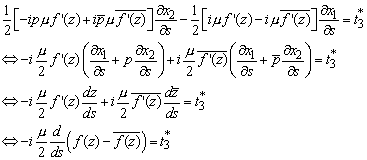
and integrating both sides gives the required answer.
Solutions to selected anti-plane shear problems
All the procedures we used to solve anti-plane shear problems for isotropic solids can immediately be applied to anisotropic materials.
Uniform stress.
Without loss of generality, we
can choose a coordinate system that ensures ![]() , as discussed earlier.
In this coordinate system we have that
, as discussed earlier.
In this coordinate system we have that ![]() . Choosing
. Choosing ![]() and matching real and
imaginary parts, we see that
and matching real and
imaginary parts, we see that
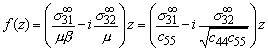
For a general orientation, we
have ![]() and a similar
calculation gives
and a similar
calculation gives
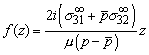
Point force in an infinite solid
We need an analytic function f(z) with single valued real part, but with multiple-valued imaginary part such that
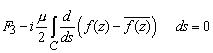
so that the tractions acting on any curve C enclosing the origin are in equilibrium with the point force F.
![]() is clearly a suitable
candidate. Substituting into the force
balance equation shows that
is clearly a suitable
candidate. Substituting into the force
balance equation shows that ![]()
Screw Dislocation
The same approach can be used to obtain stresses due to a screw dislocation – evidently
![]()
produces a displacement field with a jump of magnitude b across a branch cut that coincides with the positive real axis.
Screw dislocation near a free surface
Without loss of generality, we
place the stress free boundary along ![]() . Note that the
traction free boundary condition may be expressed as
. Note that the
traction free boundary condition may be expressed as
![]()
along ![]() .
.
Consider ![]() where d is a real constant. Evidently this solution consists of two
dislocations located at
where d is a real constant. Evidently this solution consists of two
dislocations located at ![]() and at
and at ![]()
Then
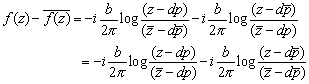
is clearly zero along ![]() and so f(z) satisfies our boundary
condition. This gives the solution for
a dislocation at a distance d below
the surface of a half-space.
and so f(z) satisfies our boundary
condition. This gives the solution for
a dislocation at a distance d below
the surface of a half-space.
Hole of radius a at the origin of an infinite solid subjected to uniform remote stress
Again, without loss of generality
we can choose a coordinate system such that ![]() . We can write the
solution as the sum of a uniform stress and a correction g(z) that will free the boundary of the hole from traction:
. We can write the
solution as the sum of a uniform stress and a correction g(z) that will free the boundary of the hole from traction:
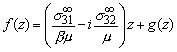
The solution must satisfy ![]() on
on ![]() , and
, and ![]() as
as ![]() . Let
. Let ![]() , and note that
, and note that
![]()
The inverse mapping
![]()
is helpful for future reference.
On the boundary of the hole ![]() , so that
, so that
![]()
This evidently describes an
ellipse, with semiaxes a and ![]() . We can map this
boundary to the unit circle with the conformal transformation
. We can map this
boundary to the unit circle with the conformal transformation
![]()
The boundary condition now
reduces to ![]() on
on ![]() . We can satisfy this
boundary condition in the usual way – expanding the function
. We can satisfy this
boundary condition in the usual way – expanding the function ![]() as a Laurent series,
and substituting into the boundary condition gives
as a Laurent series,
and substituting into the boundary condition gives
![]()
where
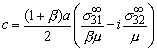
Comparing coefficients of powers
of ![]() , and using the condition that
, and using the condition that ![]() , we see that
, we see that
![]()
with all other ![]() . We therefore obtain
. We therefore obtain
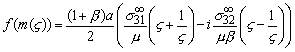
The displacements follow as the
real part of ![]() . The stresses can be calculated from the relation
. The stresses can be calculated from the relation
![]()
where
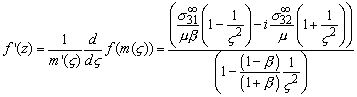
The spatial coordinates
corresponding to each value of ![]() can be calculated
with the mappings
can be calculated
with the mappings
![]()
![]()
Crack in an infinite solid under remote loading
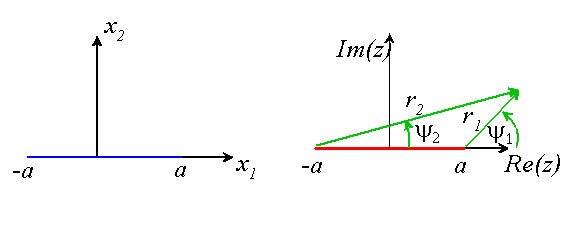
Motivated by the similarity between isotropic and anisotropic solutions we try a solution of the form
![]()
where the branch cut for the
square root is taken to lie on the real axis along ![]() . The constants c and b are to be determined.
Evidently, to give the correct stress at
. The constants c and b are to be determined.
Evidently, to give the correct stress at ![]() we must take
we must take
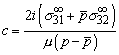
The constant b must be chosen to ensure that ![]() on
on ![]() . Recall that
. Recall that
![]() . Thus
. Thus
![]()
For ![]() the right hand side
must be purely real. For the last term
to be real, we must ensure that
the right hand side
must be purely real. For the last term
to be real, we must ensure that ![]() (b is pure imaginary), and in addition
(b is pure imaginary), and in addition ![]() , so that
, so that ![]() . The solution is
therefore
. The solution is
therefore
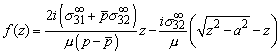
The asymptotic crack tip fields
can be computed by setting ![]() and expanding for
small
and expanding for
small ![]() , which gives
, which gives
![]()
We see the usual square root singularity at the crack tip – with no oscillatory singularity. Stress intensity factors can be defined in the usual way.