EN224: Linear Elasticity

  

 

 

Division of Engineering

    Brown University

 

 

 

 

9.4 Solutions to selected boundary value problems for anisotropic solids

 

 

Uniform stress

 

The Stroh representation for a uniform state of stress (with generalized plane strain deformation)  can be expressed in several different forms.  Note that for a uniform state of stress  and corresponding strain  we may write

In terms of these vectors the Stroh representation is given by

or, in matrix form

 

To see this, recall that a and b form eigenvectors of the fundamental elasticity matrix N as

therefore we can write (for each pair of eigenvectors/values)

Hence

Recall that

so

and finally, setting

gives the required result.

 

 

 

Point Force and Dislocation in and Infinite Solid

 

We construct dislocation and point force solutions in the usual way.  The displacements for a dislocation should be multiple valued – if we introduce a branch cut along any radial line L  from the origin, the displacements should satisfy , where b is the Burger’s vector of the dislocation.  The resultant force acting on any closed curve in the solid should vanish.  In contrast, the displacements induced by a point force (really a line load extending out of the plane) should be single valued, and the resultant force acting on any closed curve encircling the force should be equal and opposite to the point force. These conditions can be expressed as

As usual we can create the required solution using properties of log(z).  We try a solution of the form

where  and q is a vector to be determined.  Using the properties of log(z), we have that

Recalling the orthogonality properties of A and B

we can solve for q

giving

 

Some simple algebra can be used to express the displacement and stress fields in terms of the impedance tensor M.  Since M can be expressed in terms of Barnett-Lothe tensors, it can be evaluated without computing A and B, and can therefore be evaluated for degenerate materials.  To see this, note that the equations

can be solved to give

The displacement and stress function can then be computed as

In addition, we recall that M is given in terms of the (real valued) Barnett-Lothe tensors S, H, L as

 

 

Half-space subjected to prescribed tractions

 

Half-space problems can be solved using the same analytic continuation procedure that we developed for isotropic elasticity.

 

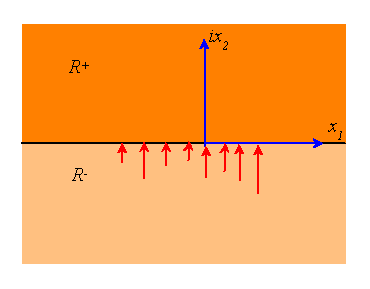
We assume that the solution is to be found in the upper half-plane , and that the solution will be expressed using the Stroh representation

where

and

is a vector of functions (analytic in  ) to be determined.  Following the usual procedure, we first devise an analytic continuation that automatically generates a solution such that the real axis is traction free.  This requires

This can be expressed as

The function on the left is analytic in , while the function on the right is analytic in .  We therefore conclude that

is analytic everywhere.  We can therefore set

To set up a solution with prescribed tractions on the real axis we must find f’(z) satisfying

which can be expressed in terms of  as

This is a Hilbert problem, with solution

The stresses and displacements can then be determined from  as

where .  The expression for  can also be expressed in a form that does not involve the eigenvalues p using the expression

which leads to

 

 

 

Point force and dislocation near a free surface

 

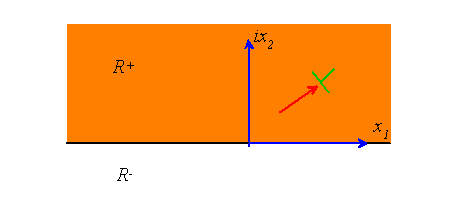
The procedure outlined in the preceding section can be used to construct the solution to a point force and/or dislocation in an anisotropic half-space.  Assume that the singularity lies in the upper half-plane.

 

We will construct the solution as the sum of the solution to a dislocation/point force in an infinite solid, together with a correction that is added to satisfy the traction free boundary condition.

 

We can denote the solution to a point force/dislocation in an infinite solid by a vector of complex functions , where

where  and  denotes the position of the dislocation/point force.  The singularities induce tractions

The corrective solution will be derived from a complex function  following the procedure outlined in the preceding section.  The function must satisfy

Note that  is analytic in  and  is analytic in .  Therefore, setting

satisfies

and therefore satisfies the boundary conditions.  The solution can be written in a unified form by recalling the continuation established in the preceding section

whence .  The combined infinite space solution with the corrective solution can be expressed as

with tractions and displacements obtained from g using the usual expressions

.

 

 

Crack in an infinite anisotropic solid under prescribed crack-face tractions

 

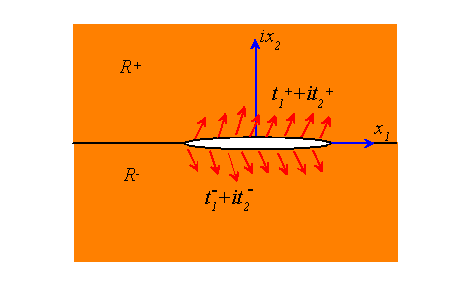
This problem can be solved using exactly the same analytic continuation that we used to solve the corresponding problem for an isotropic material.  The solution will be constructed using vectors of two analytic functions  which are analytic in , respectively.  The functions must generate a continuous displacement and traction across the real axis, which requires that

We obtain a suitable continuation by rearranging these conditions in terms of functions , which are analytic in

which shows that

are analytic in the whole plane.  These equations can be solved for the vectors .  In view of the boundary conditions, it is convenient to express the results as

 

We can simplify these conditions by defining a (real valued) matrix  G in terms of the impedance tensors for the solid

in which case

 

We now return to the boundary conditions on the crack faces

Noting that we can use the continuation to set , and using a similar expression for  we find that the boundary conditions reduce to

Subtracting the second equation from the first, and using the definition of G, we see that

whence

where Q(z) is an arbitrary vector of analytic functions.  If the stresses vanish at infinity, then Q(z)=0.  If, in addition, the tractions acting on the crack faces are equal and opposite, we see that .

 

For the particular case of equal and opposite tractions  acting on the crack faces, the governing equation for the remaining complex potential reduces to

Since  is related to  through  it is convenient to let  in which case the governing equation reduces to

This is a Hilbert problem – the different components in h decouple – and can be solved in the usual way

where , P(z) is an arbitrary polynomial, and it is understood that  denotes for the three components of h. If tractions vanish at infinity then P(z)=0.

 

For the particular case of a uniform traction, we find that the various components of h are

where  denote the components of traction acting on the upper crack face. Tractions and displacements can then be computed as

The tractions on  for  are of particular interest.  Clearly

We see the usual square-root singularity at the crack tip.  Stress intensity factors can be defined in the usual way

giving results that are identical to those for an isotropic solid.  Although the stresses along  are identical in both isotropic and anisotropic solids, the full crack tip fields differ.

 

 

Interface crack between two anisotropic solids

 

 

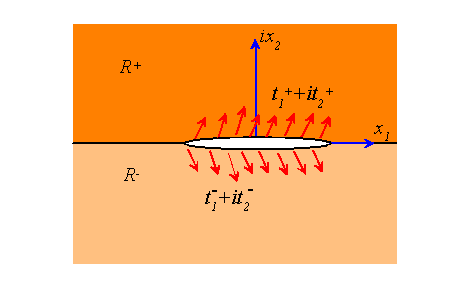
The solution for an interface crack between two anisotropic solids can be constructed using the same method.  We characterize the two materials using the Stroh matrices , with corresponding notation for all matrices derived from these.  The solution will be constructed using vectors of two analytic functions  which are analytic in , respectively.

 

As usual, our first order of business is to find a continuation that satisfies traction and displacement continuity across the interface.  Traction and displacement continuity follow as

We obtain a suitable continuation by rearranging these conditions in terms of functions , which are analytic in

which shows that

are analytic in the whole plane.  These equations can be solved for the vectors .  As before, it is convenient to express the results as

 

Again, we can simplify these conditions by defining a bi-material matrix G in terms of the impedance tensors for the two solids

in which case

 

 

We now return to the boundary conditions on the crack faces

Noting that we can use the continuation to set , and using a similar expression for  we find that the boundary conditions reduce to

Subtracting the second equation from the first, and using the definition of H, we see that

whence

where Q(z) is an arbitrary vector of analytic functions.  If the stresses vanish at infinity, then Q(z)=0.  If, in addition, the tractions acting on the crack faces are equal and opposite, we see that .

 

For the particular case of equal and opposite tractions acting on the crack faces, the governing equation for the remaining complex potential reduces to

Since  is related to  through  it is convenient to let  in which case the governing equation reduces to

This is a vector valued Hilbert problem, but the components decouple only if G is real.  If not, some further manipulations are required before the problem can be solved.  The equations may be decoupled by diagonalizing , as follows.  We first calculate eigenvectors  and eigenvalues  satisfying

or equivalently

Since G is Hermitian, the eigenvalue-eigenvector pairs have a special structure: ,    where  is real.  In terms of  and eigenvalues  we define

We can therefore write the Hilbert problem as

Finally, define  to get

The equations for the three components of g now decouple, and are thus standard Hilbert problems.  The equations for the three components of g can be expressed as

The three equations are solved using the usual procedure.  Recall that the Plemelj function  satisfies , so dividing both sides of the first equation by  and using this result gives

so choosing  gives

The solutions for the remaining components of g can be calculated the same way.

 

Because of the structure of the three eigenvalues of , the powers  appearing in the Plemelj functions also have a very special structure.  We find that

These three values of  determine the structure of the asymptotic crack tip fields.  Because two of the  values are complex,  and  give rise to oscillatory crack tip singularities that resemble those for a crack on the interface between two isotropic solids.  The solution associated with  is just the square-root singularity encountered in homogeneous materials.