 EN224:
Linear Elasticity
EN224:
Linear Elasticity
Division of Engineering
Brown University
9. Solutions for anisotropic materials
9.1 General Principles: Constitutive law and field equations
We turn next to develop the theory of elasticity for anisotropic solids. The theory is far less well developed for anisotropic materials than it is for isotropic solids. Apart from a few special cases, almost all the known solutions are two-dimensional (plane strain or anti-plane shear). Even simple 3D problems such as a point force in an infinite solid or on the surface of a half-space are generally only known in Fourier transform space. The theory is still evolving, however, and a small but dedicated group of elasticians have made substantial progress in recent years.
Here, we will present briefly the various techniques and analytical solutions that are available today. We will summarize approaches to solving plane problems first, before turning to 3D boundary value problems.
Constitutive Equation
The constitutive equation for anisotropic materials has the form where are components of stress, and are the components of the infinitesimal strain tensor. The elasticity tensor has symmetries .
For anisotropic materials the constitutive equations are best expressed in matrix form. Thus, we write
where , etc. The inverse has the form
Note that the vector definitions of strain and stress used in this section differ slightly from our earlier formulation (for consistency with Ting `Anisotropic Elasticity’)
Basis changes
The material constants or for a particular material are usually specified in a basis with coordinate axes aligned with particular symmetry planes (if any) in the material. When solving problems involving anisotropic materials it is frequently necessary to transform these values to a coordinate system that is oriented in some convenient way relative to the boundaries of the solid. Since is a fourth rank tensor, the basis change formulas are highly tedious, unfortunately. We will list them below for completeness.
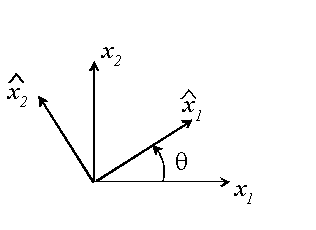
To this end, let us suppose that the components of the stiffness tensor are given in a basis , and we wish to determine its components in a second basis, . We define the transformation tensor with components , or in matrix form
This is an orthogonal tensor satisfying . In practice, the tensor can be computed in terms of the angles between the basis vectors. It is straightforward to show that stress, strain and elasticity tensors transform as
The basis change formula for the elasticity tensor is more conveniently expressed in matrix form as
where the rotation matrix K is computed as
where the modulo function satisfies
Although these expressions look cumbersome they are quite convenient for computer implementation.
The basis change for the compliance tensor follows as
where
The proof of these expressions is merely tiresome algebra and will not be given here. Ting’s book (1996) has a nice clear discussion.
For the particular case of rotation through an angle in a counterclockwise sense about the axes, respectively, the rotation matrix reduces to
where . The inverse matrix can be obtained simply by changing the sign of the angle in each rotation matrix. Clearly, applying the three rotations successively can produce an arbitrary orientation change.
9.3 Governing Equations
Our mission is to find solutions to the Navier equation of elasticity
subject to the usual boundary conditions. In subsequent discussions, we will largely need to abandon index notation and instead use matrix notation. Thus, the equilibrium equations will be written as
Plane deformations
We now seek either anti-plane shear solutions of the form , or plane strain deformations of the form .
Note first that such solutions cannot exist in general anisotropic materials. We will first establish the conditions necessary for the existence of plane deformations.
For anti-plane shear deformations the equilibrium equations reduce to
The three equations cannot all be satisfied by the same displacement; moreover elastic constants must satisfy . Thus, anti-plane shear deformations can exist if and only if
The governing equation is thus
For Plane strain deformations the equilibrium equations reduce to
In this case, can be chosen to satisfy two out of the three equations, but not all three. The elastic constants must satisfy . Consequently, the third equation can only be satisfied by setting
The governing equations for plane deformations are
Plane deformations therefore only exist in a material with elastic constants and orientation satisfying
The most common class of crystals – cubic materials – satisfies these conditions for appropriate orientations.