 EN224:
Linear Elasticity
EN224:
Linear Elasticity
Division of Engineering
Brown University
2D plane solutions for Anisotropic Elasticity
We now consider the more complex case of 2D deformation. The formulation of anisotropic elasticity is still evolving – a recent contribution is Choi et al International Journal of Solids and Structures 40 (2003)1411 –1431. There are strong indications that the solution techniques used today are not the best one – for example with today’s representations, coordinate transformations lead to very strange contortions in the solutions; and the invariance of quantities such as hydrostatic stress are not apparent in the algebraic solutions. Moreover, there are some materials (including isotropic and transversely isotropic materials) for which the formulation blows up. Issues such as completeness of representations need to be addressed. Nevertheless, the Stroh formulation – presented below with some modifications - is the most commonly used version of anisotropic elasticity
Stroh representation of solutions
As always, we are looking for solutions to the Navier equation
We have already seen that strict plane strain deformation solutions can only exist for special materials and orientations. For a general anisotropic solid we must therefore relax the plane strain constraint, and seek generalized plane strain solutions of the form
The Stroh solution proceeds along the lines we followed to obtain anti-plane shear solutions. We set with p a complex number to be determined, and seek solutions of the form
where is a vector to be determined. We see that
whence the governing equation can be expressed as
This can be re-written as
or in matrix form as
where
The matrix equations have nontrivial solutions if
Since Q, R and T are 3x3 matrices, this is a sextic equation for p, with 6 roots. For positive definite materials p is always complex, so the 6 roots are pairs of complex conjugates. The corresponding eigenvectors - which also play a central role in the following development – must also appear as pairs of complex conjugates.
The most general solution to the displacement field may therefore be expressed as
where are the three pairs of complex roots of the characteristic equation; are the corresponding eigenvalues, and are analytic functions.
The original Stroh formulation, as extended and described in Ting’s book on anisotropic elasticity, uses the full expansion for u. However, since u must be real, not all the solutions obtained in this way are of interest. Most known solutions have the form
where
and use the eigenvalues with positive real part, and are the corresponding eigenvectors. Although known solutions do seem to have this structure, to my knowledge the completeness of this representation has not been proved.
Stresses
The stresses can be obtained from the constitutive equation
where we recall that for each of the six characteristic solutions we may obtain displacements as , so that
where Q, R and T were defined earlier. Define
and note that the governing equations require that
Therefore, for each member of the family of solutions, we can obtain stresses from
The symmetry of the stress tensor requires that
Ting simplifies the expression for stresses by defining a vector valued stress function
whence
but this is not particularly helpful.
The general expression for stresses then follows by summing the six separate eigensolutions:
Resultant force on an arc
The stress function is related to the resultant force exerted by tractions acting on an arc in the solid
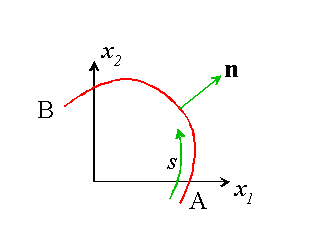
The resultant force (per unit out of plane distance) acting on an arc AB due to tractions acting on the outward normal of the arc can be computed as
Matrix form of solutions
There are various matrix representations for displacements and stresses, as follows. Following the procedure outlined above, we define
and define the characteristic equation for the system through
are the three pairs of complex roots of the characteristic equation with positive and negative imaginary part, respectively; are the corresponding eigenvalues, and let . We then introduce normalized matrices of combinations of the eigenvectors as follows
In addition, define
Then
Most solutions have the form . In this case, we may write
where
are the tractions acting on planes with normals in the and directions, but again I am not aware of a proof that this representation is complete.
Obviously, while the eigenvalues p are uniquely defined for a particular set of elastic constants, the eigenvectors are not unique, since they may be multiplied by any arbitrary complex number and will remain eigenvectors. It is sometimes helpful to normalize the eigenvectors so that the matrices A and B satisfy
but this can result in very cumbersome expressions for A and B (although it generally simplifies expressions for the solutions) and is not absolutely necessary.
Eigenvalues and anisotropy matrices for cubic materials
Since the eigenvalues p for a general anisotropic material involve the solution to a sextic equation, an explicit general solution cannot be found. Even monoclinic materials (which have a single symmetry plane) give solutions that are so cumbersome that Maple 8 simply bombs. The solution for cubic materials is manageable, as long as one of the coordinate axes is parallel to the direction. If the cube axes coincide with the coordinate directions, the elasticity matrix reduces to
whence
The characteristic equation therefore has the form
giving
whence
For the eigenvalues are purely imaginary. The special case corresponds to an isotropic material.
The matrices A and B can be expressed as
These matrices have not been normalized to ensure that . Instead
These quantities can also be expressed in terms of the engineering constants. Recall that for cubic materials the constitutive equation can be expressed as
and in terms of , we have
and we may define an anisotropy factor . For A=1 the material is isotropic. In terms of these parameters
while
Degenerate Materials
There are some materials for which the general procedure outlined in the preceding sections breaks down. We can illustrate this by attempting to apply it to an isotropic material. In this case we find that
, and
The eigenvalues are repeated, and there only two independent eigenvectors a associated with the repeated eigenvalue , and so the representation of displacements and stress is not complete.
The physical significance of this degeneracy is not known. Although isotropic materials are degenerate, isotropy does not appear to be a necessary condition for degeneracy, as fully anisotropic materials may exhibit the same degeneracy for appropriate values of their stiffnesses.
Choi et al have found a way to re-write the complex variable formulation for isotropic materials into a form that is identical in structure to the Stroh formulation. This approach is very useful, because it enables us to solve problems involving interfaces between isotropic and anisotropic materials, but it does not provide any fundamental insight into the cause of degeneracy, nor does it provide a general fix to the problem.
In some cases problems associated with degeneracy can be avoided by re-writing the solution in terms of special tensors (to be defined below) which can be computed directly from the elastic constants, without needing to determine A and B.
Fundamental Elasticity Matrix
The vector and corresponding eigenvector can be shown to be the right eigenvectors and eigenvalues of an unsymmetric matrix known as the fundamental elasticity matrix, defined as
where the matrices
were introduced earlier. Similarly, can be shown to be the left eigenvector of N.
To see this, note that the expressions relating vectors a and b
can be expressed as
Since T is positive definite and symmetric its inverse can always be computed. Therefore we may write
and therefore
This is an eigenvalue equation, and multiplying out the matrices gives the required result.
The second identity may be proved in exactly the same way. Note that
so
again, giving the required answer.
For non-degenerate materials N has six distinct eigenvectors. A matrix of this kind is called simple. For some materials N has repeated eigenvalues, but still has six distinct eigenvectors. A matrix of this kind is called semi-simple. For degenerate materials N does not have six distinct eigenvectors. A matrix of this kind is called non semi-simple.
Orthogonal properties of A and B
The observation that and are right and left eigenvectors of N has an important consequence. If the eigenvalues are distinct (i.e. the material is not degenerate), the left and right eigenvectors of a matrix are orthogonal. This implies that
In addition. the vectors can always be normalized so that
If this is done, we see that the matrices A and B must satisfy
Clearly the two matrices are inverses of each other, and therefore we also have that
These results give the following relations between A and B
Barnett-Lothe tensors
From the preceding section, we observe that
Therefore and are pure imaginary, while the real part of . The three matrices defined by
are therefore purely real. These matrices will be shown to transform as tensors under a change of basis. They are known as Barnett-Lothe tensors.
Many solutions can be expressed in terms of S, H and L directly, rather than in terms of A and B. In addition, Barnett and Lothe devised a procedure for computing S, H and L without needing to calculate A and B. Consequently, these tensors can be calculated even for degenerate materials.
For cubic materials, with coordinate axes aligned with coordinate directions, one can show that
where
In terms of engineering constants defined earlier, we can set
The Impedance Tensor
The impedance tensor M relates A and B through the definition
M or its inverse appears in the solution to many problems. It can be expressed in terms of Barnett-Lothe tensors using formulas given in the next section, and so can be calculated for degenerate materials.
Useful relations between matrices in anisotropic elasticity
We collect below various useful algebraic relations between the various matrices that were introduced in the preceding sections.
Recall that a matrix satisfying is Hermitian. A matrix satisfying is skew-Hermitian.
· is skew Hermitian. To see this, note that the orthogonality relations for A and B require that
· is Hermitian. This follows trivially from the preceding expression.
· and are both Hermitian. To see this, note and use the preceding result.
· The matrices are Hermitian. To show the first expression, note that and recall that L is real. A similar technique shows the second.
· are both orthogonal matrices. To see this for the first matrix, note that , where we have used the orthogonality properties of B. A similar procedure shows the second result.
· The impedance tensor can be expressed in terms of the Barnett Lothe tensors as
To see the first result, note that and use the definitions of H and S. The second result follows in the same way. Note that H, L and S are all real, so this gives a decomposition of M and its inverse into real and imaginary parts. In addition, since we can compute the Barnett-Lothe tensors for degenerate materials, M can also be determined without needing to compute A and B explicitly.
· . To see these, note that M and its inverse are Hermitian, note that the imaginary part of a Hermitian matrix is skew symmetric, and use the preceding result.
Basis Changes
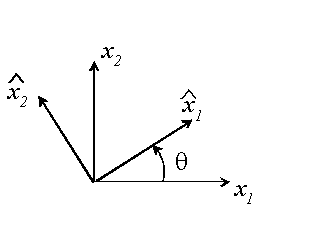
We obtain a number of additional useful results by finding basis change formulas for the various elasticity matrices defined in preceding sections.
To this end, consider a basis change that involves rotating the axes through angle about the axis.
It is straightforward to show that
where
The transformation relations for elasticity matrices Q, R and T can be expressed as
where are computed as
where , and are the components (in the basis) of the stiffness tensor and unit vectors parallel to and , respectively. Alternatively
or
To see these, note that coordinates and displacements transform as vectors, so that
consequently
which directly gives the basis change formula for A.
To find the expression for p, we note that
so that can thus both functions of and . Since we conclude that
as required.
The basis change formulas for Q, R and T follow directly from the definitions of these matrices.
The basis change formula for B is a bit more cumbersome. By definition
Substituting for gives
and finally recalling that we obtain the required result.
The basis change formulas for the Barnett-Lothe tensors and impedance tensor follow trivially from their definitions. The basis change formulas justify our earlier assertion that these quantities are tensors.
Barnett-Lothe integrals
The basis change formulas in the preceding section lead to a remarkable direct procedure for computing the Barnett-Lothe tensors directly, without needing to calculate A and B. The significance of this result is that, while A and B break down for degenerate materials, S, H, and L are well-behaved. Consequently, if a solution can be expressed in terms of these tensors, it can be computed for any combination of material parameters.
Specifically, we shall show that S, H, and L can be computed by integrating the sub-matrices of the fundamental elasticity matrix over orientation space, namely, let
and define
Then
To see this, we show first that can be diagonalized as
where
and was defined earlier. From the preceding section, we note that
which can be expressed as
as before, we can arrange this into an Eigenvalue problem by writing
whence
This shows that [a,b] are eigenvectors of the rotated elasticity matrix. Following standard procedure, we obtain the diagonalization stated.
Now, we examine more closely. Recall that
Integrating gives
(the sign of the integral is determined by Im(p) because the branch cut for is taken to lie along the negative real axis).
Thus,