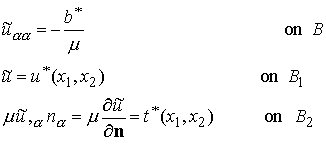EN224: Linear Elasticity
EN224: Linear Elasticity 
Division of Engineering
5. 2D Static Boundary Value Problems II: Anti-Plane Shear
We proceed to develop approximate solutions to boundary value problems in elasticity.
One can induce states of anti-plane shear in a solid by loading it in a special way. We rarely actually load solids so as to cause them to deform in anti-plane shear. However, we will find that the governing equations and boundary conditions for anti-plane shear problems are beautifully simple: we end up solving Laplace’s equation! Many powerful techniques are available to do this. Whenever you are faced with solving a complex linear elastic boundary value problem (and are unwilling to resort to numerical methods), you should consider setting up a similar anti-plane shear problem first. Your solution will have many of the features of the more general case, and may help you see how to solve the more complex problem too.
5.1 Field Equations and Boundary Conditions
We will discuss anti-plane shear in the context of a three-dimensional boundary value problem.
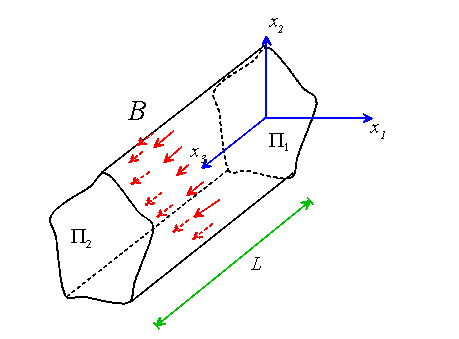
Consider a cylindrical solid with arbitrary cross-section, as shown in the figure. Assume that the length of the cylinder L greatly exceeds any cross sectional dimension. Consider the following boundary value problem:
Find![]()
with
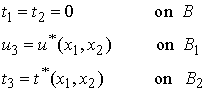
With
for a traction boundary value problem.
The boundary conditions on ![]() are left in weak form:
are left in weak form:
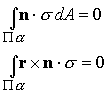
i.e. we accept any solution with zero resultant force and moment acting on the ends of the cylinder.
Recall the field equations
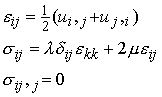
Since all forces and displacements are prescribed to act in the ![]() direction on the boundary of the solid, it is
natural to assume that the displacements are in the
direction on the boundary of the solid, it is
natural to assume that the displacements are in the![]() direction everywhere.
Thus, try a solution of the form
direction everywhere.
Thus, try a solution of the form
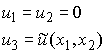
The strains and stresses follow as
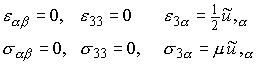
and so the equilibrium equations reduce to
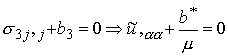
The boundary conditions may be re-written as
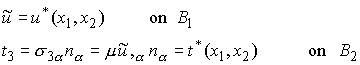
Summary:
To solve an anti-plane shear problem, we assume
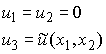
where