EN224: Linear Elasticity       

   Division of Engineering

 

3.8 Axisymmetric Contact

 

One of the most successful applications of linear elasticity has been to predict the behavior of two solids in contact. The results have provided a basis for designing gears, bearings, cams, wheels, continuously variable transmissions, etc, etc.

We will use the results developed in the preceding section to solve some axisymmetric contact problems. Begin with the simplest case.

 

Lubricated flat punch indenting a half-space.

 

 

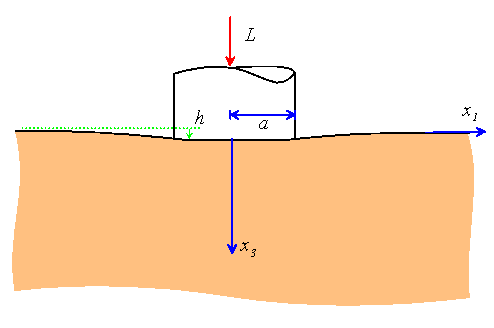
We seek with

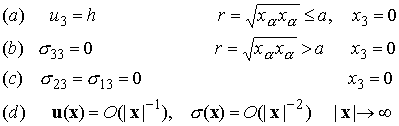
We will solve this problem using two approaches.

 

Solution via integral equations

 

First, note that we may use the results of Sect. 3.7 to compute the fields in a half-space subjected to an arbitrary distribution of pressure on its surface. We could ask: what pressure distribution should act on the surface of the half-space in order to satisfy the boundary conditions?

 

From the preceding section, we see that the surface displacement due to a unit point force at the origin is

 

 

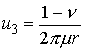
Thus, we seek an axisymmetric contact pressure distribution that satisfies

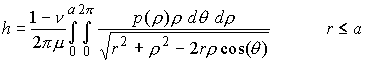
It is not a trivial exercise to solve this equation, unfortunately. One may readily verify that

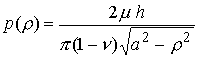
satisfies the equation.

 

Solution via complex stress functions

 

A particularly elegant formulation for axisymmetric contact problems has been developed by Love, Green and Zerna, Collins, and Hill. Recall that we are looking for a harmonic potential that satisfies

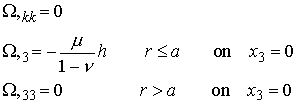
Consider the complex harmonic function

where

It is straightforward to show that

The integrals and derivatives of this function are also harmonic.

Consider

On the surface:

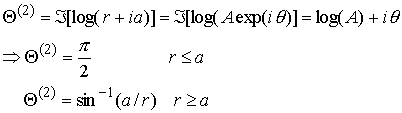
also

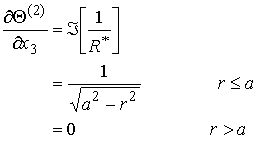
Thus, choosing

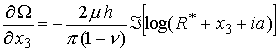
will satisfy all our boundary conditions. This expression can be integrated to obtain the potential: Mathematica comes up with the expression

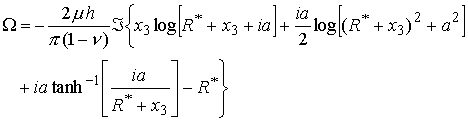
which can probably be simplified further, but I am too lazy (any offers?)

The contact pressure is of particular interest:

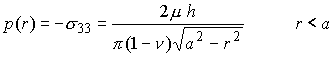
The load applied to the punch follows as

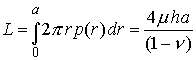
Note that the punch has a well-defined compliance: indentation tests are sometimes used to measure elastic properties of thin films (the compliance is measured while unloading the indenter, to try to minimize the effects of plastic flow).

Note also that the displacement of the surface outside the area of contact follows as

 

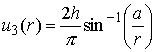
General frictionless axisymmetric contact

There are various ways to generalize these results to punches with a rounded profile, see e.g. Green and Zerna and the discussion in Barber (refs given in list of texts). A particularly appealing approach was discovered by Hill, and we will outline his argument below.

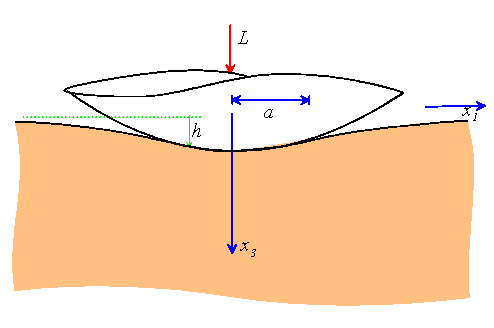
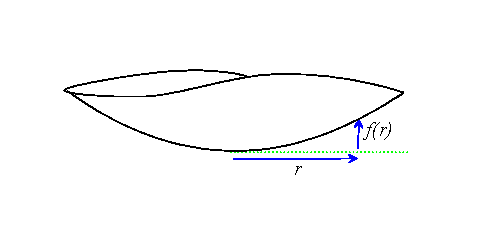
We now suppose that a punch with a rounded nose is pressed into the surface of an elastic half-space. Let denote the punch profile, and assume that f is a monotonically increasing, differentiable function of radius r. For example, we could choose

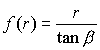
To describe a conical punch with semi-angle , or use

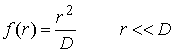
to approximate a spherical punch, diameter D (we have approximated the punch by a parabola, with the expectation that the radius of contact is small).

 

We now seek

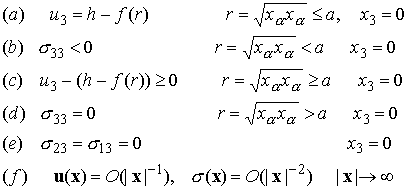
Note that several additional constraints have been introduced here. In contact problems, the area of contact is not known a priori and must be determined as part of the solution. Additional constitutive assumptions must be made to specify how the two contacting surfaces interact, in order to ensure that the contact area may be uniquely determined.

Here, we have assumed that the interface between the punch and the half-space cannot withstand any tension (this is based on experiment: when you touch a surface, you generally don’t stick to it).

A primary objective, then, is to determine the relationship between penetration depth h and contact radius a. Actually, we will try to solve for the inverse relationship: given a, we will try to find a function h(a) such that h=h(a).

We will solve the general punch problem using a clever idea known as cumulative superposition: we recognize that we should somehow be able to superpose the axisymmetric punch solution in some way so as to produce the solution we need. Let us see if we can work out how to do this.

Suppose that we already know for a particular value of h.

Let for this h. Now, suppose we increase the depth of penetration

We will try to find the resulting change in S , i.e.

find

with

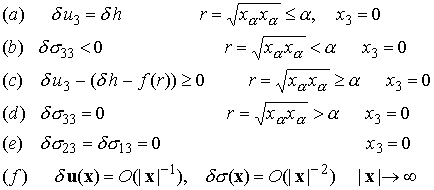
Observe that (a), (b), (d) (e) and (f) are identical to the boundary conditions for the flat punch problem we just solved. We can only check that (c) is satisfied if we are given f, but it is clearly satisfied for any punch whose profile can be described as a power law.

We will accept the flat punch solution as . Then

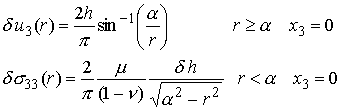
Now, we suppose that we may reach the current indentation depth h by a succession of increments which take the contact radius from to

The displacement of a point on the surface outside the area of contact follows as

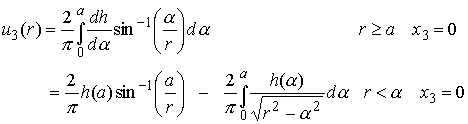
The second line was obtained by integrating the first by parts.

In particular, if we evaluate this expression at r=a, we find

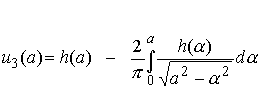
Recall that boundary condition (a) requires

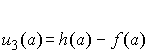
so we conclude that our unknown contact radius-penetration depth relation must satisfy

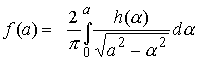
This is an Abel integral equation, and can be inverted explicitly, as follows

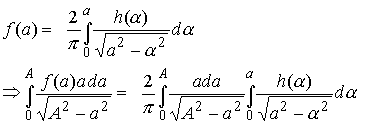
Reverse the order of integration for the double integral on the right hand side

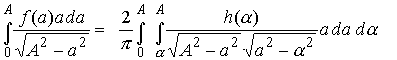
The integral with respect to a may now be evaluated, giving

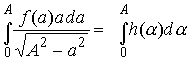
so that

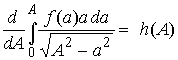
Integrate by parts and note that f(0)=0, then evaluate the derivative to obtain

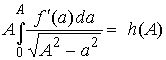
where

This gives part of the solution: we now know the relationship between penetration depth and contact radius. The contact pressure distribution follows as:

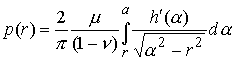
The load applied to the indenter may now be computed

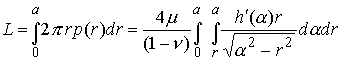
Again, one may switch the order of integration to obtain

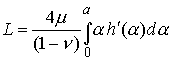
One can continue this procedure to derive an explicit expression relating the load to the punch profile f, but we won’t do so here.

In principle, we could determine the full stress and displacement fields in the half-space. We could either use the known contact pressure distribution, together with the solution for a point force on a half-space to find the result we need, or attempt to integrate the potentials for the flat punch. In either case, the integrals are generally non-trivial, but exact results are known for both conical and spherical indenters. For the conical indenter, see Sneddon, I.N., `Fourier Transforms,’ McGraw Hill, 1951; for the spherical indenter, see Hamilton, G.M., `Explicit expressions for the stresses beneath a sliding, spherical indenter,' Proceedings of the Institution of Mechanical Engineers, 197C, 53, (1983).

 

Example

We will compute the contact radius and contact pressure for a spherical (parabolic, actually) indenter.

Approximate the profile by

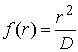
where D is the diameter of the indenter. Then

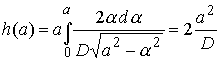
or,

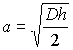
The contact pressure distribution follows as

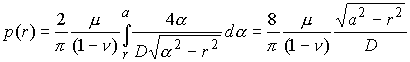
and the load

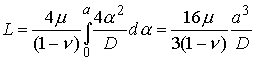
We may re-write this in terms of the depth of penetration h:

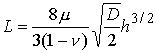
Observe that the load-displacement relation is nonlinear. Observe that the stiffness of the contact is

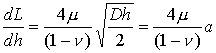
i.e., the contact stiffness as a function of contact radius is identical to that of a flat punch on a half-space. It is straightforward to use the results listed earlier to show that this is in fact a general result, independent of the profile of the punch f(r).

 

The stress fields under the indenter scale with the maximum contact pressure. Examine the expression for the contact pressure to see that

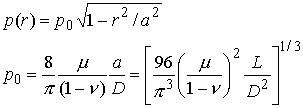
Note that stresses scale as the cube root of the load: doubling L only produces a 26% increase in the stress. This is one reason that wheels work so well. The other is that the stress state is close to hydrostatic compression everywhere, so there is little tendency for fracture or plastic flow to occur under a contact. The maximum shear stress is

and occurs on the symmetry axis at a depth 0.48a below the surface. The maximum tensile stress turns out to be

and occurs on the surface at the edge of the contact.

 

Generalized axisymmetric Hertzian contact

 

It is not difficult to generalize the results we obtained for a spherical indentor to determine the contact pressure distribution when two spherical solids (with large diameter compared to the contact radius) are pressed into contact. The details are left as a homework problem.

It is worth noting that solutions may also be computed for the more general non-axisymmetric contact; for details see Johnson, K.L., `Contact Mechanics,’ CUP 1985.