EN224: Linear Elasticity    

Division of Engineering

 

 

8.6 Application of Minimum Complementary Energy

Like the principle of minimum potential energy, the concept of minimum complementary energy is useful for obtaining approximate solutions to boundary value problems and to obtain bounds on solutions. We will illustrate the latter idea here.

Return to our favorite torsion problem

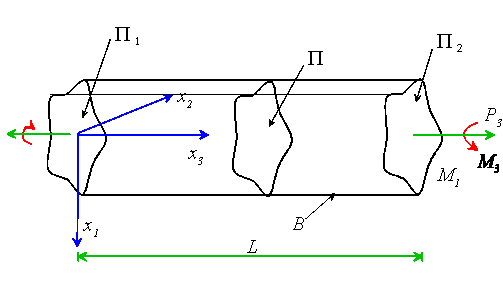
Let with

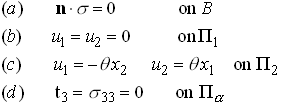
As before, we will attempt to bound the torsional stiffness k, defined such that

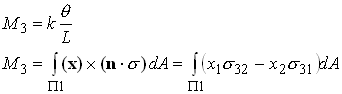
We will see that the principle of minimum complementary energy allows us to obtain a lower bound to the torsional stiffness. Begin by computing the exact complementary energy . Recall that

From the treatment in section 8.4, we already know that

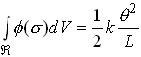
Consider the second term

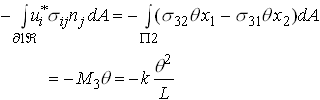
Hence

Actually, we could have obtained this result immediately, since it is a general result that Can you show this?

Now, let be the components of a statically admissible stress field, which satisfies

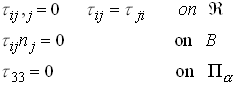
Then, we know that , so that

Consequently, we can obtain a lower bound to k with any statically admissible stress state.

The question is, how do we generate an appropriate state of stress? Well, since we’re dealing with a two dimensional region, we can generate equilibrium stress fields using Airy stress functions. For example, we could take

with all other stress components zero. This is clearly an equilibrium field and satisfies , but we still need to satisfy the boundary condition on B.

We can find a straightforward way to do this. Observe that the boundary condition may be expressed as

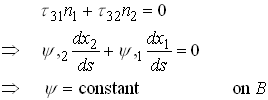
Next, let us express C in terms of . Observe that

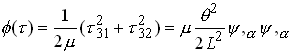
Similarly

so that

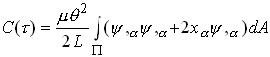
We therefore obtain the following lower bound to k

Now, we want to find a scalar potential , with on B, which maximizes our lower bound. Note that we may adjust both the magnitude and the distribution of to get the best lower bound. Actually, for a given distribution, we can calculate the magnitude exactly. Consider a family of functions , with a scalar: we can then find the value of to maximize the lower bound. Write

where

Evidently is a minimim (and hence maximizes k) for

Thus

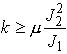
Finally, to obtain a bound for k, we need to choose a suitable . Any function that is constant on the boundary will do. Of course, we could choose =constant, but that gives us k=0 and we know we could probably do better. For a simply connected section, we could try

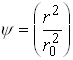
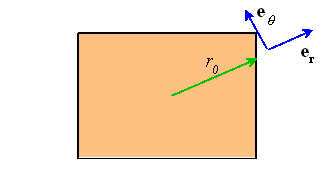
where is the distance from the origin to the perimeter of the cross section, as shown below

Hence

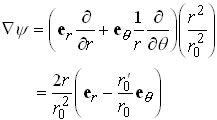
where

so that

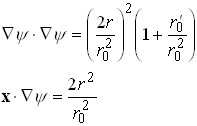
Substitute into the expressions for and to see that

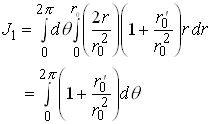
and

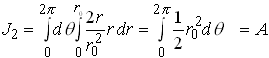
where A denotes the cross sectional area of the section.

Finally, we see that

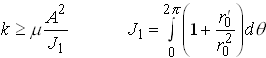
It is a straightforward exercise to compute k for a given cross section. For example, for a circular section, we find

which is of course the exact solution.

 

As an exercise, you might like to compute lower and upper bounds to the stiffness of a shaft with square cross section, and then compare the bounds with the exact solution given in Section 4.2.