EN224: Linear Elasticity     

Division of Engineering

 

7.2 Boundary Conditions for Plane Complex Potentials

When we worked out complex variable representations for anti-plane shear problems, we found that the boundary conditions on the complex potentials could be expressed in a very convenient and simple form. For displacement boundary value problems, the real part of the complex potential had to take on prescribed values on the boundary , while for traction boundary value problems, the complex potentials were related to the resultant forces acting on the boundaries of the solid. We find very similar results for plane elastostatic solutions too. We proceed to work out the details.

 

Displacement Boundary Value Problems

Let be a plane elastostatic state, satisfying boundary conditions

where is a prescribed complex function.

Then, the complex potentials defined in the preceding section must satisfy

 

Proof: follows from the definition of the complex potentials.

 

 

Traction Boundary Value Problems

It takes a bit more work to set up boundary conditions for traction boundary value problems. As before, let be a plane elastostatic state, satisfying

Define

The complex potentials defined in Section 7.1 must satisfy

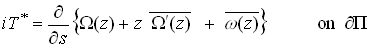
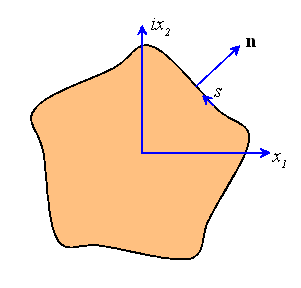
Where s denotes arc length around the boundary, with positive direction defined so that the solid always lies on the left as you travel in the direction of increasing s, as shown in the figure.

Equivalently

 

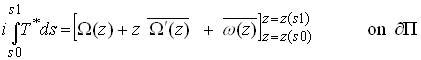
Proof:

Write the boundary conditions as

Recall that

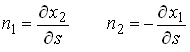
Therefore

Now, recall the expressions for stress fields in terms of complex potentials

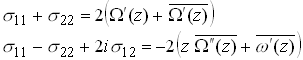
so that

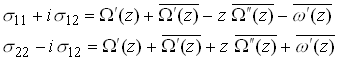
The boundary conditions may therefore be expressed as

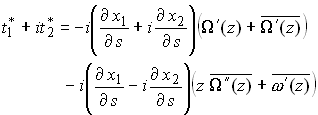
Now, note that

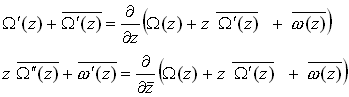
and furthermore

so that

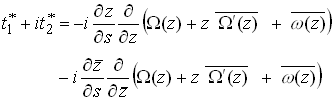
whence

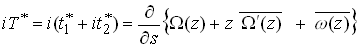
Observe that the boundary conditions for both displacement and traction boundary value problems may be expressed in unified form:

Where

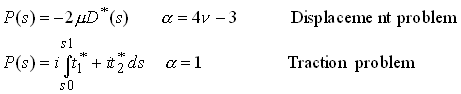
The arbitrary choice of s0 in the integral reflects the fact that displacement fields for traction boundary value problems are not unique; one can only find D to within a rigid body motion.