EN224: Linear Elasticity    

Division of Engineering

 

7.5 Calculating Complex Potentials Using Cauchy Integral Formulae

 

There are some problems that are best solved by expanding the complex potentials as Taylor or Laurent series. This procedure works best if only a few terms in the series are needed. Otherwise, one often makes better progress by applying the Cauchy integral formulae. This procedure actually gives exact solutions for any displacement or traction boundary value problem, although the resulting integrals can be hard to evaluate unless the solid can be mapped conveniently to the unit circle.

We will illustrate the idea by using it to solve the problem of a circular disk subjected to arbitrary traction or displacement on its boundary.

We will assume that the disk has unit radius, without loss of generality.

Following the procedure outlined in Sections 7.1 and 7.2, then, our objective is to find complex potentials satisfying

With

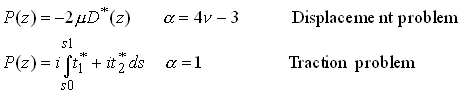
Evidently

 

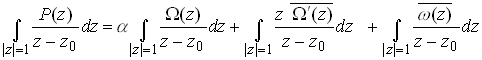
Where is any point within the disk.

Now, consider the three terms on the right hand side of this expression. Applying the Cauchy integral formula directly shows

To evaluate the second term, expand the complex potential as a Taylor series (we know this can be done, since the potentials must be analytic within the disk).

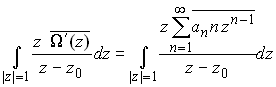
Now, since on |z|=1, we have

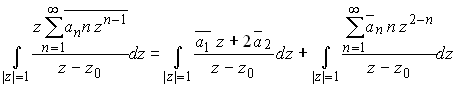
The first integral on the right hand side may be evaluated directly using the Cauchy integral formula. The second term may be shown to be zero, using residues, as follows. Recall that if a function f(z) has a simple pole of order m at , then

where

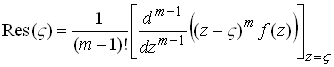
Apply this to the particular case

 

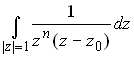
This has a simple pole of order n at z=0 and a pole of order 1 at , so

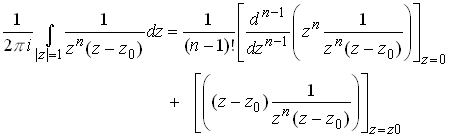
wherupon

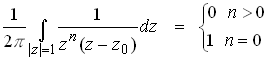
Thus

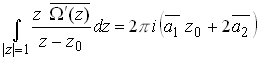
Next, consider

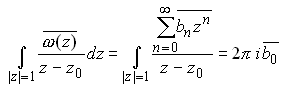
The complex potentials can only be determined to within an arbitrary constant, even for a displacement boundary value problem – you can clearly add a constant c to and subtract from and still generate the same displacement field. Thus, we may set

without loss of generality.

Let us collect the information that we’ve obtained so far. Substituting back for the three integrals we evaluated, we see that

 

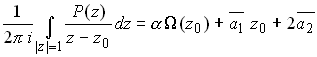
We are close to finding a closed form expression for , but we still need to find some way to determine the constants . To do this, expand as a Taylor series

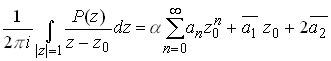
Differentiate this expression with respect to , and set in the result

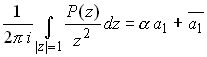
Similarly, differentiate with respect to twice, and set

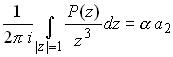
For a displacement boundary value problem, the preceding two expressions may be solved for For the traction boundary value problem, one can only determine and the real part of , because in this case. This is to be expected, since we can only determine the potentials to within an arbitrary rigid body motion. One may set the imaginary part of to zero in this case.

 

For future reference, we note that we can determine the first coefficient in the Taylor series using the same idea. Simply set :

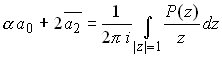
We have now determined . We still need to find , however. To do this, rearrange the boundary conditions to

We can use the Cauchy integral formula again to evaluate within the disk

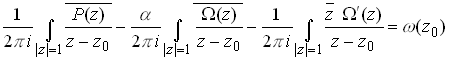
Since we’ve already determined this is good enough, but it can actually be simplified: the second two integrals may be evaluated by expanding as a Taylor series, with the result

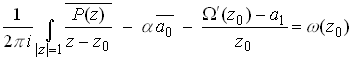
The details are left as an exercise.

 

Summary

 

The closed form solution to a displacement or traction boundary value problem for a disk of unit radius is

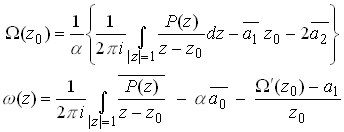
With

 

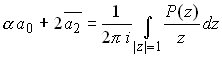
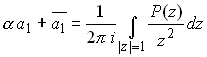
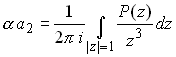
For traction boundary value problems, it is not necessary to evaluate and

Note that we can add any complex constant to both and and still generate the same stress field, since only derivatives of potentials appear in the expressions for stresses.

Therefore, we could add to and to without changing the stress field. If we do this, the expressions for the potentials only involve P and

 

Example

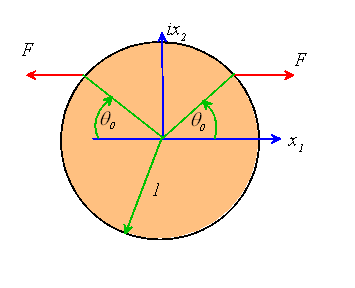
We will use this procedure to determine the solution for a disk subjected to concentrated loads on its boundary, as shown below.

We begin by evaluating P. Recall that

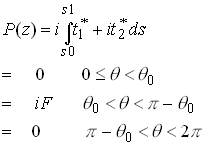
Since this is a traction boundary value problem, we may set as discussed earlier. Then,

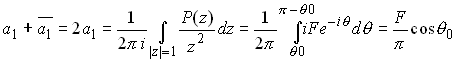
Next,

Similarly

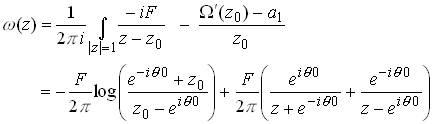
Amazing!

Clearly, the same idea can be used to solve problems involving a circular hole in an infinite solid, subjected to prescribed traction or displacement on its boundary.