EN224: Linear Elasticity  

Division of Engineering

 

 

Application of Analytic Continuation: Traction Boundary Value Problems for the Half-Plane

 

We now return to the traction boundary value problem we posed earlier. Find the displacements and stresses in a half-space due to a prescribed distribution of traction on its surface.

We will use the representation based on stress continuation to derive our result. Evidently, we need to find a potential which is analytic in both R+ and R-, and satisfies

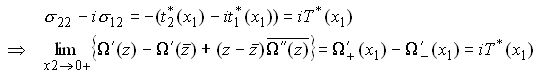
(we assumed that

here, which can only be verified after we have a solution).

Thus, we need to find a potential with a prescribed discontinuity on the real line.

 

It looks like we are stumped here, but actually this problem has a well-known solution.

To solve the problem, we make use of the Plemelj formulae, for which we will need some more results from the general theory of complex variables.

 

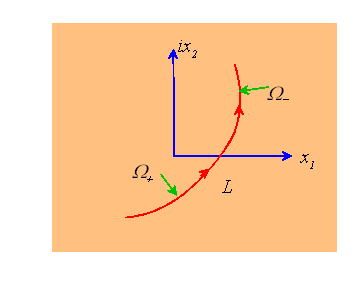
The Plemelj formulae

Let be a complex valued function defined on an arc L. Assume that satisfies the Holder conditions on L, that is:

for any two points , where A is a positive constant and

Then

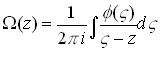
is sectionally analytic in a region R cut along L; that is to say, satisfies the following conditions:

    (1) is analytic on {R-L}
(2) is sectionally continuous in the neighborhood of L
     (3) At an end of the arc L, satisfies

Furthermore, the limiting values may be shown to exist on L and satisfy

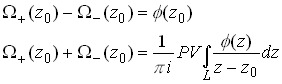
Where PV denotes that the integral should be interpreted as a Cauchy Principal Value (the integral is singular because z0 lies on L). These two equations are the Plemelj formulae. For a proof of these results, you could consult Muskhelishvili `Singular Integral Equations,’ Dover reprint.

These results provide the key to solving the half-plane problem. The most general solution satisfying our boundary condition is

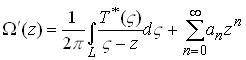
We added the polynomial here because any continuous analytic function on R evidently generates zero traction on the surface. If the stresses vanish at infinity then .

 

Example: Determine the potentials generating displacement and stress fields in a half-plane loaded by uniform pressure p and shear s on the region –a<x1<a.

 

Evidently

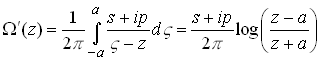
And hence

Displacement and stress fields may be then determined from

 

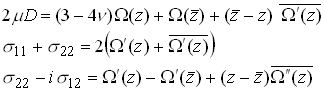
Example: Fields induced by point forces beneath the surface of a half-plane.

 

Here is another useful trick which exploits the idea of analytic continuation.

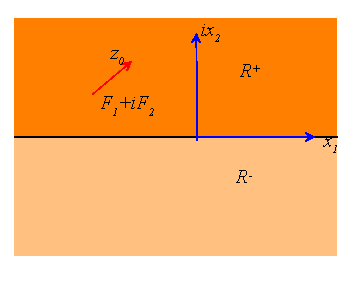
A half-plane with traction free surface is subjected to a point force acting at a point . Determine complex potentials for this problem.

 

Recall that the potentials

 

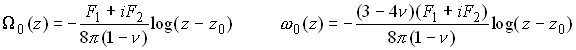
ogether with the standard complex variable formulation (no continuation, that is to say) generated the fields associated with a point force acting at z0 in an infinite solid.

 

On the real line, these forces induce stresses

We must therefore superpose an additional solution which generates equal and opposite tractions on the surface of the half-plane. We could apply the procedure outlined in the preceding subsection to do this, but it is quicker to get the solution directly. Suppose that the corrective solution is to be generated by a potential , using the stress continuation discussed earlier. Then

Now, observe that is analytic in R-, while is analytic in R+.

We may therefore satisfy the boundary conditions by setting

 

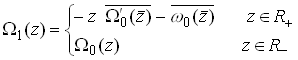
This solves our problem, but it is inconvenient to have part of the solution expressed using the standard complex variable representation, while the corrective term is expressed using the formulation based on stress continuation across the real axis. We can write the correction in the standard form by computing . Recall that

so that

(Note that whenever we evaluate we need to decide whether its argument lies in R+ or R-. Since z lies in R+, is in R-. )

Then, finally, we may write

giving

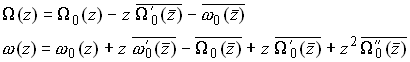
Stresses and displacements should be evaluated using the standard representation

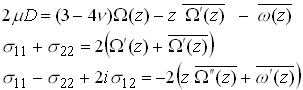
ensuring that both z and z0 are in R+

 

Exactly the same approach may be used to find the fields due to a dislocation near a free surface. Alternatively, using displacement continuation, we may compute the fields due to a dislocation near a rigid boundary.