EN224: Linear Elasticity    

Division of Engineering

 

7.3 Simple Examples of Complex Potentials

Here are two examples of complex potential representations for two dimensional elastostatic states.

 

Line load in an infinite solid

 

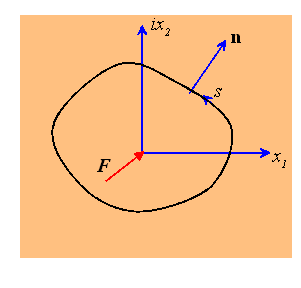
Findwith

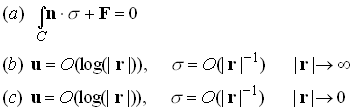
When we solved the anti-plane shear version of this problem, we found that f(z)=log(z) produced a displacement field of the correct form. It is worth trying the same thing here.

Suppose that

where A and B are complex coefficients, to be determined. Both potentials are analytic everywhere except at the origin.

These potentials clearly satisfy conditions (b) and (c) above. In addition, the displacement field must be single valued. Recall that

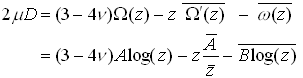
Note that

so we must set

to ensure that the displacement field is single valued.

Finally, we need to satisfy condition (a). We may compute the resultant force acting on any closed curve within the solid using the results obtained in Section 7.2. Thus, choosing the unit circle as a special case

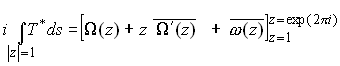
whence

 

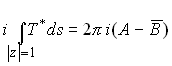
We must select A and B so that

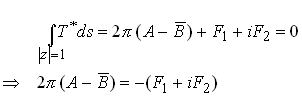
Where F is the magnitude of the force acting at the origin.

Finally, solving for A and B shows that

 

 

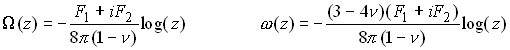
Edge Dislocation in an Infinite Solid

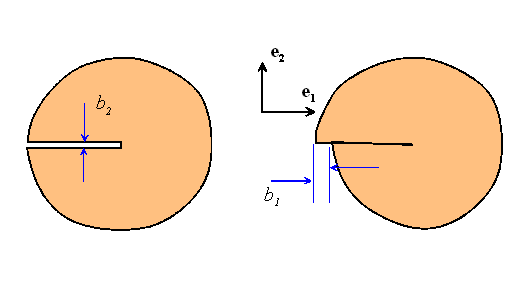
Our potentials for a point force evidently have the potential (excuse me) to generate multiple valued displacement fields. Indeed, they can be combined to generate a displacement field with a constant jump across any radial branch cut. This is the displacement field associated with an edge dislocation in an infinite solid.

Thus, choose A and B so that

(the sign convention for the Burger’s vector b is arbitrary. The statement above defines what we mean by a positive Burger’s vector).

This requires

For the dislocation, we require the resultant force on any closed curve to vanish. From the point force problem, we see that this requires

Solving for A and B shows that