 EN224: Linear Elasticity
EN224: Linear Elasticity 
Division of Engineering
7.4 Calculating Complex Potentials Using Taylor and Laurent Series
We have seen that solutions to plane problems in elastostatics can be reduced to two analytic potentials on the region of interest. It would be nice to find a general procedure to determine these complex potentials.
Our experience with anti-plane shear problems suggests that we might pursue three possible approaches: (1) try expanding our solution as a Taylor series; (2) try applying the Cauchy integral formulae, and (3) try conformal mapping.
The Taylor series approach is identical to the procedure we followed when solving anti-plane shear problems, and we will only briefly summarize the procedure here (you will use this approach to solve a problem in Homework 5).
Recall that displacement and traction boundary value problems are reduced
to the following problem. Determine analytic functions![]() which are analytic
on the region of interest, and satisfy
which are analytic
on the region of interest, and satisfy
with
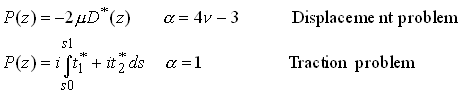
For a simply connected region, we may expand P and our complex potentials as Taylor series, i.e.
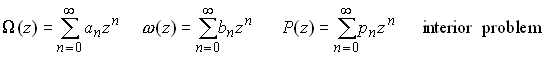
then substitute into the boundary conditions for the complex potentials,
and solve for the unknown complex constants![]() by comparing coefficients
of powers of z.
by comparing coefficients
of powers of z.
When expanding P, the following result is helpful:
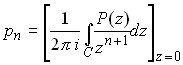
Where C is any contour enclosing the origin.
For a multiply connected region, we have to be a bit more cautious. We saw in the preceding section that the complex potentials are multiple valued, if the resultant force on any arc in the solid is nonzero. Tractions may act inside holes in a solid, and the resultant force on each hole need not necessarily be zero. The most general form of the complex potentials for a multiply connected region is
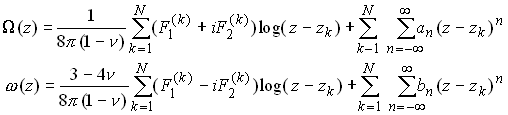
where N is the number of holes in the solid;![]() is a point anywhere
inside the kth hole and
is a point anywhere
inside the kth hole and ![]() are the components of the resultant
force acting on the kth hole.
are the components of the resultant
force acting on the kth hole.