EN224: Linear Elasticity 
Division of Engineering
3.4 Solutions for 3D dislocation loops in an infinite solid.
The Kelvin state, together with the reciprocal theorem, provides a neat way to determine fields associated with dislocation loops.
First, recall what is meant by a dislocation. We can introduce a dislocation
into an elastic solid by cutting it over a surface, and then imposing a
uniform displacement
across the two sides of the cut. Here b
represents the Burger’s vector of the dislocation.
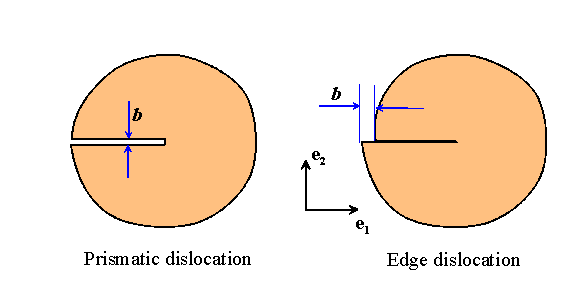
We can easily visualize dislocations in 2D
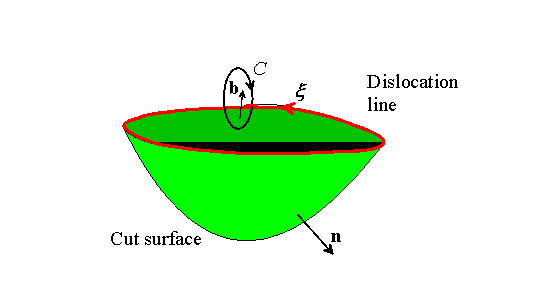
The same idea works in 3D, as illustrated in the picture. A general
dislocation is defined by a line direction
and it’s Burger’s
vector b. There is more than one sign convention for defining the
positive sense of and b: here, we will adopt the following convention.
First, choose a positive sense for . Then, to visualize the Burger’s
vector, choose a point somewhere in the solid and describe a Burger’s
circuit around the dislocation line in a direction consistent with the
right hand screw convention, as shown in the picture below. Because the
displacement field is multiple valued, the displacement at the start of
the circuit differs from that at the end of the circuit . We will define
. Thus, for the 2D dislocations shown above, we would set
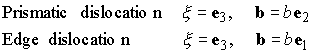
Now, our objective is to compute the displacement and stress fields associated with a general 3D dislocation loop in an infinite solid. Once again, we will do this using the reciprocal theorem
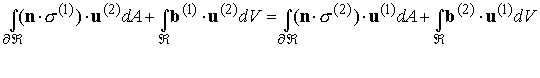
For the dislocatiaon, identify the boundaries 
with the upper
and lower surfaces of the cut.
Let us choose
And take
to be the fields associated with the dislocation loop.
Now, apply the reciprocal theorem,
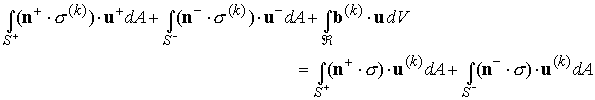
Here,
and 
denote the upper and lower surfaces
of the cut, as shown in the figure; while
denotes the outward
(i.e. pointing away from the solid) normal to and 
denotes the outward
normal to . Similarly, 
and 
denote the displacement
associated with the dislocation loop on the upper and lower surfaces of
S.
Now, note that
Furthermore, 
(the displacement associated with the Kelvin state)
is continuous and so is equal on the two sides of S. Recall also
that the body force field for the Kelvin state is a delta distribution
centered at
Finally, use the symmetry of the Kelvin state and note
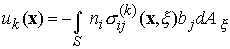
To determine stress componentes, we may differentiate under the integral sign to conclude
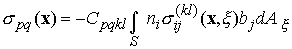
where
are the doublet states.
This gives us a procedure for computing stress fields for arbitrary dislocation loops. Actually, it turns out that this expression can be simplified: we could anticipate this since we know that the dislocation fields depend only on the shape of the dislocation line and its Burger’s vector, and not on the surface S. Thus, there should be some way to reduce the surface integral to a line integral around the boundary of S. Stoke’s theorem provides a way to do this, but the algebra involved is so tiresome that we will merely give the final result here
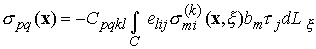
where
where denotes the tangent to the dislocation line.
For further details, see: Mura, T. Phil Mag. 8 (1963) p.843; Int J. Eng Sci, 1 (1963), 371;
Willis J. Int J. Eng Sci., 5 (1967), 171.