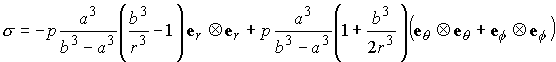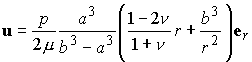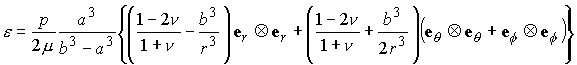EN224: Linear Elasticity     

       Division of Engineering

1.5 Field Equations Implied by the Fundamental System

We now derive several auxiliary field equations which follow as a consequence of the field equations listed in the preceding section. These field equations will be useful when we begin to develop techniques for solving boundary value problems.

Strain Equations of Compatibility

Motivation: When we solve boundary value problems in linear elasticity, we sometimes solve for the stress field (for example, we may use an Airy stress function to generate a solution), and then need to deduce the displacement field. How do we do this?

Alternatively, we might ask the question: are all equilibrium stress fields admissible solutions to linear elastic boundary value problems? The answer is, not necessarily. Given the stress, one could compute a distribution of strain in the solid. However, not all strain distributions can be derived from a displacement field. Below, we list the conditions necessary and sufficient to guarantee that a strain distribution can be derived from a displacement field.

Let u be and on

Then             (1)

Or               

Or               

Proof: Substitute into any of the above, and use smoothness of u, together with a liberal dose of algebra.

Conversely, if is simply connected, and is a symmetric tensor field satisfying (1) on
Then there exists a displacement field u satisfying

Furthermore, given the strain field, we can compute the displacement field as follows:

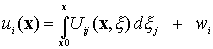
Where

 And represents a rigid body displacement.

To use this expression, we first choose a point x0 in the solid that we will regard as fixed. Then w=0. Next, we compute . Finally, we evaluate the integral to deduce the displacement at an arbitrary point x. Note that we can evaluate the integral along any convenient path, since it must be path independent.

Proof:

Show first that the integral is indeed path independent. This requires that be a perfect differential. This is the case as long as

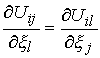
It is straightforward to show that this is true:

The last expression evidently vanishes if the strains are compatible.

Next, show that

Evidently

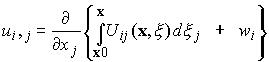
Recall that for a general function f(x,x)

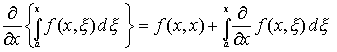
So that

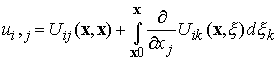
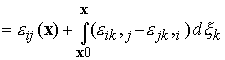
The integrand is evidently skew in i and j, so confirming our assertion.

Compatibility for multiply connected regions

 The compatibility conditions outlined in the preceding section do not guarantee single valued displacements in a multiply connected domain, for the following reasons.

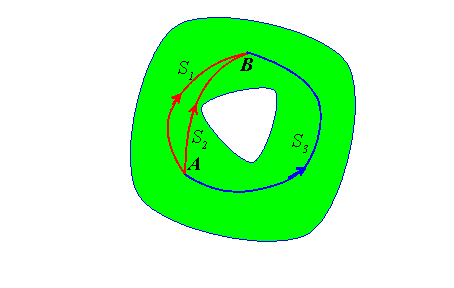
Our check for path independence of guarantees only thataround any infinitesimal closed path C.

This can be used to show that the integral is path independent for any topologically similar path: e.g. integrating along S1 is equivalent to integrating along S2. This is because you can perturb S1 to S2 by a sequence of infinitesimal perturbations.

The compatibility conditions do not guarantee that integrating along S1 is equivalent to integrating along S3: no infinitesimal perturbations can shift S1 to S3 without leaving the solid.

Stress equations of compatibility (elastostatics)

We now turn to our second question: are all equilibrium stress fields solutions to elastostatic boundary value problems? Evidently, there must be a compatible distribution of strain associated with an admissible stress field. It is straightforward to rewrite the restrictions on the strain field in terms of stresses, at least for an isotropic solid.

Let be a simply connected, isotropic, linear elastic solid. Denote the elastic shear modulus with m and denote Poisson’s ratio by n . Let [u,e,s] be an elastostatic state on with body force field b.

Then

 

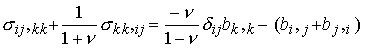
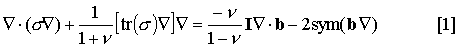
Conversely, let s be a symmetric two tensor field on satisfying and [1] above. Let

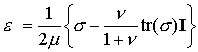
Then there exists a displacement field u satisfying

 

Proof: put e in terms of s in and simplify using

Sufficiency: put e into [1] and reverse argument.

 

Displacement Equations of Motion (Cauchy-Navier)

It is often convenient to rewrite the linear momentum balance equation in terms of displacements rather than stresses. For a general solid

For an isotropic solid, we may substitute for C:

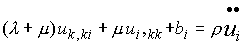
Or, equivalently

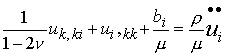
In more general notation:

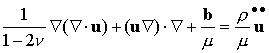
A Simple Boundary Value Problem

Before proceeding, we will illustrate the steps one must follow to solve a boundary value problem by looking at a simple problem.

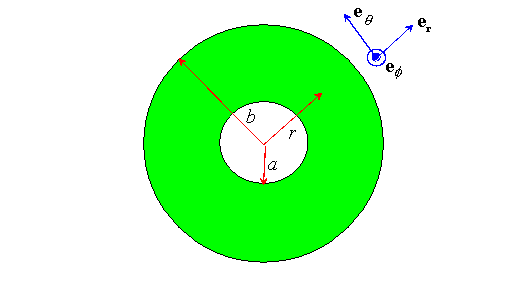
Let be a thick walled spherical shell, with inner radius a and outer radius b. Assume that the shell is made from an isotropic, linear elastic solid. Assume that the inner wall of the shell is subjected to a normal pressure p, while the outer surface is traction free. Find the displacement, strain and stress fields in the solid.

This is a static boundary value problem. We must solve the field equations listed in section 1.4, with boundary conditions

The problem is straightforward because of symmetry. Assume that the displacement field has the formwhere u(r) is a function to be determined.

Substitute into the Navier equation. To this end, recall that the gradient operator in spherical-polar coordinates may be expressed as

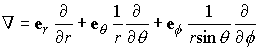
Recall also that

Hence

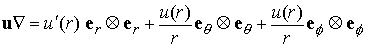
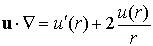
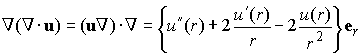
So that the Navier equation reduces to

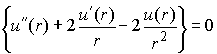
To solve this, observe that

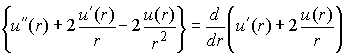
So that

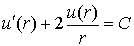
Note that

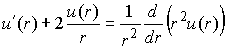
So, finally

The constants A and B must be determined from the boundary conditions. To this end, note that

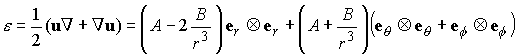
For an isotropic solid, the constitutive law in general notation has the form

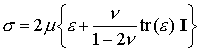
So the stress is

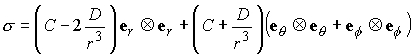
Where

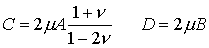
Substituting into the boundary conditions shows that

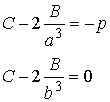
Which may be solved for C and B.

Finally, the full solution is given by