 EN224:
Linear Elasticity
EN224:
Linear Elasticity 
Division of Engineering
3.6 Eshelby Inclusion Problems
Eshelby found an important application of the results outlined in the preceding section.
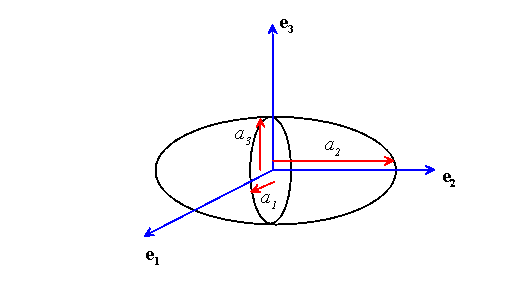
Consider an infinite, homogeneous, isotropic, linear elastic solid.
Suppose we introduce a uniform eigenstrain![]() in the ellipsoidal
region
in the ellipsoidal
region
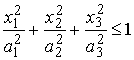
We can use the procedure outlined in the preceding section to compute the fields in the solid. For our present application, the body force is zero everywhere except on the surface of the ellipsoid, where the body force is singular
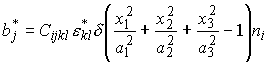
Where n denotes the normal to the ellipsoid.
The integrals for the potentials cannot be evaluated exactly (except for the special case of a spherical region) but they can be reduced to elliptic integrals.
Remarkably, it turns out that the strain and stress fields inside the ellipsoid are uniform. Outside the ellipsoid, the fields are more complex, but can still be reduced to expressions involving a small number of elliptic integrals.
We will give results only for fields within the ellipsoidal region here. The total strain is usually expressed as
where ![]() is a function of the elastic properties of the solid
and the semi-axes of the ellipsoid, and is known as the Eshelby tensor.
Its components are comlicated, but here they are (at least for an isotropic
solid)
is a function of the elastic properties of the solid
and the semi-axes of the ellipsoid, and is known as the Eshelby tensor.
Its components are comlicated, but here they are (at least for an isotropic
solid)
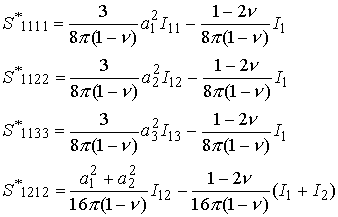
The remaining components may be computed by the cyclic permutation of
(1,2,3). Any components that cannot be obtained in this way are zero: thus![]()
Assume that![]() . Then, the Is may be computed from
. Then, the Is may be computed from
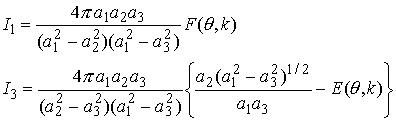
where E and F denote the elliptic integrals
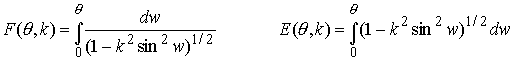
and
The remaining functions follow from the identities:
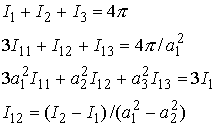
Outside the ellipsoid, the strains are nonuniform, but it is possible to reduce the results to a form that involves only three elliptic integrals. The results are too lengthy to be recorded here, but details may be found in Mura, T., `Micromechanics of defects in solids,’ Martinus Nijhoff, 1982.
For the special case of a spherical inclusion, these results reduce to a very simple form
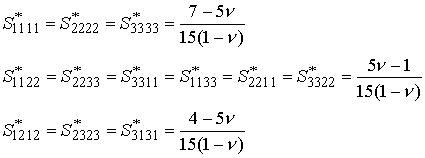
All other components are zero.
The stress state may be deduced from
Ellipsoidal Inhomogeneities.
The fields due to eigenstrains are of little interest in their own right. They are mainly of interest because they provide the key to computing the strains and stresses within a second phase particle surrounded by an elastic matrix. This solution is of considerable importance in estimating the properties of composite materials.
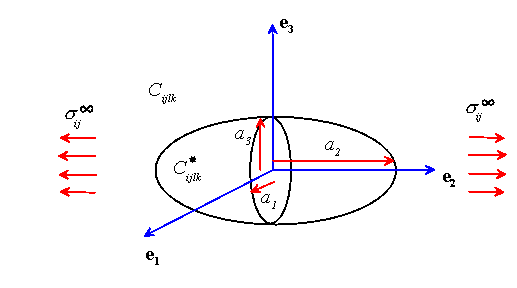
Consider an infinite solid, which contains an ellipsoidal inhomogeneity, as illustrated in the picture. Suppose that in the region
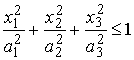
the elastic constants are ![]() , while outside this region, they
are
, while outside this region, they
are![]()
Assume that the solid is subjected to a remote stress and strain
Our objective is to compute![]()
with
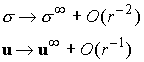
As![]()
We regard the solution to consist of two terms:
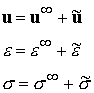
Here,![]() is the state that would be induced by the remote loading
if the solid were homogeneous with elastic constants corresponding to the
matrix, and
is the state that would be induced by the remote loading
if the solid were homogeneous with elastic constants corresponding to the
matrix, and![]() corrects the solution for the presence of the inclusion.
corrects the solution for the presence of the inclusion.
We will compute the correction![]() by turning the problem involving
the inhomogeneous region into an equivalent one, which involves a homogeneous
solid containing a transformation strain inside the region occupied by
the inclusion.
by turning the problem involving
the inhomogeneous region into an equivalent one, which involves a homogeneous
solid containing a transformation strain inside the region occupied by
the inclusion.
Observe that![]() satisfies all the field equations everywhere, except
for the constitutive relations inside the inclusion. Furthermore, note
that the error in the stress
satisfies all the field equations everywhere, except
for the constitutive relations inside the inclusion. Furthermore, note
that the error in the stress
is uniform inside the region occupied by the inclusion. This suggests that we could correct the solution by superposing the state of stress induced by a uniform transformation strain within the ellipsoidal region inside a homogeneous solid. Let us see if this works.
In the actual solid, we require
We anticipate that ![]() will be uniform inside the inclusion.
will be uniform inside the inclusion.
Now correct ![]() by adding a transformation strain inside the ellipsoidal
region. Within the inclusion,
by adding a transformation strain inside the ellipsoidal
region. Within the inclusion,
Evidently, to produce the correct stress inside the inclusion, we need to find a transformation strain that satisfies
Now, recall that in the eigenstrain problem
Where ![]() are the components of the Eshelby tensor.
are the components of the Eshelby tensor.
Substituting, we find that the transformation strains can be computed by solving
Once the transformation strains have been determined, the strains and stresses within the inclusion follow. The fields outside the inclusion may also be determined, using the lengthy expressions for stress and strains outside the transformed region. Alternatively, they could be computed by using the known displacements and tractions on the matrix/inclusion boundary, together with a judicious application of the reciprocal theorem.
Elliptical crack in an infinite solid.
The results above may be used to construct another important solution. Observe that there is nothing to stop us taking the elastic moduli inside the inclusion to be zero: in which case the `inclusion’ is actually a hole (it is stress free). The required transformation strains can still be computed, and the displacement and strain fields in the hole are nonzero. Although strains and displacements inside the hole don’t mean anything, those on the boundary of the hole are useful. For example, using the reciprocal theorem, we could write down integral expressions for the fields inside the solid. We can also use the result to determine stress intensity factors for elliptical and circular cracks inside an infinite solid. Note that by collapsing one of the semi-axes of the ellipsoid, we create a crack. The crack opening displacements may be deduced from the displacements on the surface of the ellipsoid, and by taking the appropriate limit of COD near the crack tip, one can deduce the required stress intensity factors.