EN224: Linear Elasticity

 

Homework 1: Linearized Field Equations and Constitutive Law

Due Friday Feb 18, 2005

 

Division of Engineering

Brown University

 

 

1. Consider an elastic material with reference mass density .  Suppose that, instead of characterizing the material through the specific Helmholtz free energy in terms of Lagrange strain E and temperature, we choose to express the specific Helmholtz free energy in terms of deformation gradient F, as . 

 

1.1 Follow the argument used in class to show that nominal stress (defined as in class – may be the transpose of what you are used to seeing) is related to Helmholtz free energy by

 

1.2 As a specific example, consider an elastic solid with Helmholtz free energy given by

.  Find an expression for the nominal stress in terms of F.

Linearize the constitutive law for infinitesimal motions.  Show that the linearized constitutive law characterizes an isotropic solid, and find formulas for the shear modulus and Poisson’s ratio for the linearized material in terms of A and B.

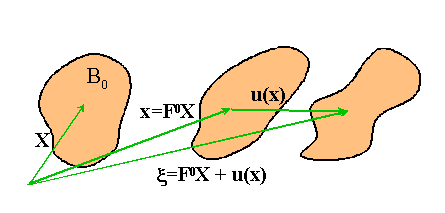
1.3 Consider a solid whose constitutive response can be characterized using the free energy in 1.2.  Suppose that the solid is first subjected to loading that induces a (time independent) homogeneous deformation .  A small additional load is then applied to the solid that induces an additional displacement field , with .  Obtain a set of linearized field equations for the displacement field and suitable strain and stress fields.  You should include (i) An appropriate linearized strain measure; (ii) an appropriate linearized stress measure, with momentum balance equations, and (iii) a linearized constitutive equation. 

2. Express the constitutive law for a linear elastic solid in matrix form as , where  and  represent column vectors of stress and strain and  represents a 6x6 elasticity matrix. 

2.1 Show that the material has a positive definite strain energy density (  ) if and only if the eigenvalues of  are all positive.

2.2 Hence, show that  is invertible for a material with positive definite strain energy density.

2.3 Calculate the eigenvalues of the compliance matrix  (where  ) for an isotropic solid in terms of Young’s modulus and Poisson’s ratio.  Hence, re-derive the restrictions on values of Poisson’s ratio and Young’s modulus that were found in class.  Find the eigenvectors of  and sketch the deformations associated with these eigenvectors.

2.4 Suppose that a cubic material is characterize by the values of ,  and  in the elasticity matrix.  Use the same approach to derive restrictions on the admissible ranges of ,  and .