EN224: Linear Elasticity

 

Homework 3: Half space problems, Eshelby Inclusions,

Due Friday March 18, 2005

 

 

 

 

Division of Engineering

Brown University

 

1.      Tangentially loaded half-space.

 

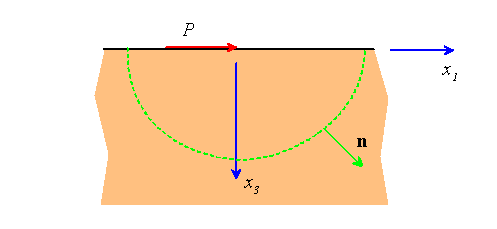
(1.1)  State the appropriate boundary conditions for a half-space subjected to a   point

          force acting tangent to its surface, as shown in the figure.

(1.2)  Examine the list of Boussinesq potentials given at the end of Sect 3.1 of the online

          lecture notes.  Consider solutions A, B and E, which generate stresses from

          harmonic potentials   as follows:

Following the procedure outlined in Sect 3.7 for a normally loaded half-space, find a way to combine solutions A, B, and E so as to generate an elastostatic state which automatically satisfies    on the surface of the half-space.  You should find you can generate the required solution from a single harmonic potential  .  Set up the boundary conditions that represent a point force at the origin.

 

(1.3) Take Fourier transforms of the governing   equations and boundary conditions

         found in (1.2).  Hence, deduce that the transform of the required potential satisfies

 

Use the result for the normally loaded half-space to write down  and hence deduce the potential  

(1.4)    Determine the displacement field for the tangentially loaded half-space.

 

 

2.  Spherical inhomogeneity. Suppose that an infinite solid with shear modulus and Poisson’s ratio  contains a spherical inclusion with shear modulus .  The solid is loaded in uniaxial tension  at infinity.  Calculate the stress, strain and displacement in the inclusion (take the displacement to be zero at the origin)

 

 

 

3.  Energetics of Eigenstrains.  Consider a homogeneous, stress free, linear elastic solid with elastic constants .  Suppose that an eigenstrain distribution   is introduced into a bounded subregion of the solid B.  Let   denote the total strain distribution in the solid.

 

Show that the total strain energy of the solid is

 

To do this, begin by writing down the strain energy within B.  Then, write down an expression for the total strain energy outside B in terms of the traction acting on the boundary of B.  Then find a way to rearrange the sum of these two terms into the form given above.

 

 

 

4. General Axisymmetric Contact. Suppose that two isotropic, linear elastic spheres

with radii   and  moduli and Poisson’s ratios                                           are pressed into contact.

 

Assume that if the two spheres did not deform, they would overlap by a distance h as shown in the figure.

 

 

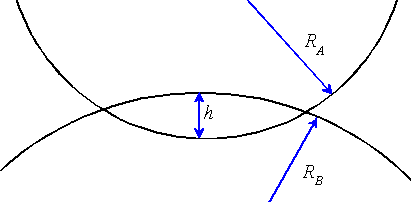
Make the following assumptions:

 

(1)  The radius of the contact area between the two spheres is much smaller than the radius of either sphere.

(2) Both spheres deform as though they were infinite half-spaces.  That is to say, the radial displacement of a point on the surface of sphere A due to a point force acting a distance r away on its surface is

(3) Approximate the profile of each sphere by a parabola.

 

Write down an integral equation for the contact pressure distribution acting between the spheres, in terms of the sphere radii and the elastic constants.

 

Compare the result with the integral equation that governs the pressure distribution acting between a rigid sphere and an elastic half-space.  Hence, find expressions for the radius of the contact area between the spheres, the contact pressure distribution and the relationship between the load P and the approach of remote points on the spheres h.