EN224: Linear Elasticity
EN224: Linear Elasticity
Homework 5: Complex variable methods for plane problems
Due Friday April 22, 2005
Division of Engineering
Brown University
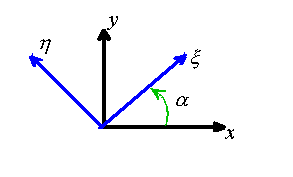
1. Let be two complex potentials that generate stresses and displacements according to the usual formulation (no continuation)
Show that the displacement and stress components in the basis shown in the figure can be calculated as
2. Complex variable solution to a pressurized cylinder.
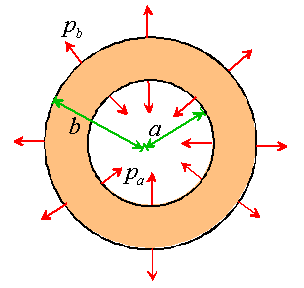
2.1 Using the results of the preceding problem, show that the complex potentials that generate stress and displacement fields in a pressurized cylinder (see above) must satisfy
2.2 By expanding and as Laurent series, find the potentials that solve this problem. To simplify the algebra, note that , and assume that the solution can be generated from terms in the series that after substitution in the boundary conditions, are independent of z.
3. Dislocation near a rigid interface
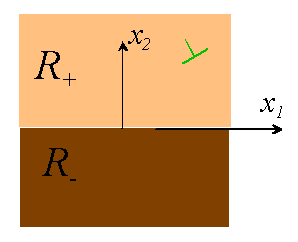
3.1 Begin by finding an analytic continuation that automatically satisfies D=0 on . To do this, start with the standard complex variable formulation
Express the boundary condition in terms of and defined in . Next, express the boundary condition in terms of potentials which are analytic in . Use the result to show that
where L denotes the real axis. Hence, conclude that this implies that
is analytic in . Use this to calculate an expression for , and hence show that a solution with D=0 on can be generated by finding a single potential that is analytic in , and calculating displacements and stresses from
3.2 Let generate the solution for a dislocation at position in an infinite solid. Deduce that, to satisfy D=0 on L, we must superpose a second potential satisfying
and calculating stresses and displacements from this potential using the formulation in 3.1.
3.3 Using (3.1) as a guide, write down the potential in terms of and
4. Stress induced by indentation with a rigid wedge
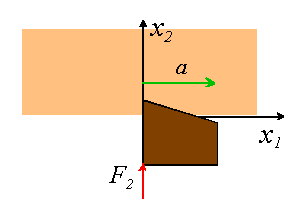
Suppose that an elastic half-space is indented by a rigid frictionless wedge, with profile . Calculate the potential that generates the stress field in the solid in terms of and . Hence, determine the contact pressure distribution and the slope of the surface for . Use the conditions that the contact pressure cannot be tensile, and the two solids cannot overlap to deduce the relationship between contact width a and the force applied to the punch.
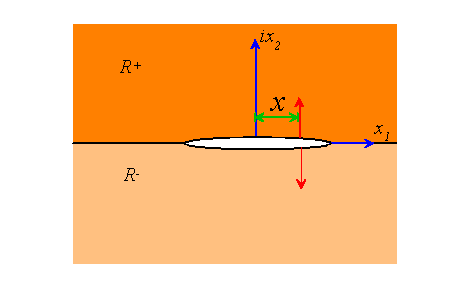
5. An alternative solution for the pressurized crack
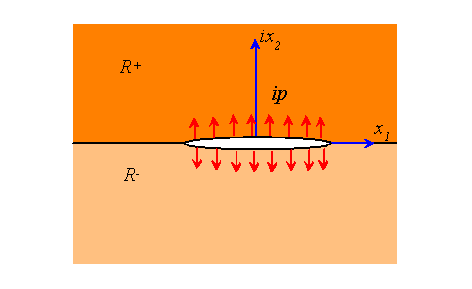
There is often more than one choice of analytic continuation for a particular boundary value problem. To illustrate this, in this problem we will devise an alternative procedure to solve the pressurized crack problem that was discussed in class.
Consider a crack that is subjected to equal and opposite tractions on its faces. Symmetry conditions imply that on outside the crack. Moreover, it is evidently sufficient to find a solution in the upper half-plane, since the solution in the lower half-plane follows by symmetry.
5.1 Starting with the standard complex variable formulation
show that setting will automatically satisfy on .
5.2 With this choice of , show that the condition that on implies that
showing that
is continuous outside the crack, and analytic in the whole plane. Deduce that .
5.3 Hence show that traction boundary condition on the crack faces leads to a Hilbert problem for
5.4 Write down the general solution to the Hilbert problem.
5.5 Hence, find an expression for the stress intensity factors induced at the right hand crack tip by a pair of equal and opposite point forces acting on the crack faces.