EN224: Linear Elasticity
EN224: Linear Elasticity
Homework 6: Energy methods, anisotropic elasticity
Due Friday May 6, 2005
Division of Engineering
Brown University
1. Let denote the solution to a linear elastostatic boundary value problem. Let and denote the potential and complementary energy, respectively.
Show that
2. Torsion
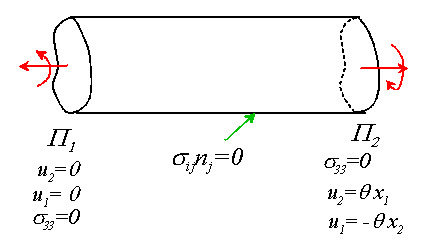
2.1 Reconsider the torsion problem discussed in class, with boundary conditions illustrated above. Using a kinematically admissible displacement field given by
obtain an expression for the potential energy of the solid.
2.2 By minimizing the potential energy, show that the best approximation to the displacements is obtained by selecting a function w that satisfies
2.3 With w given in 2.2, deduce that the stiffness of the shaft (defined as in class) must satisfy
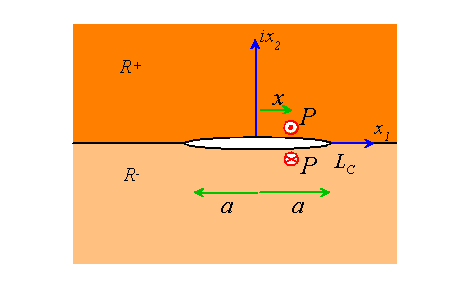
3. Interface crack between two anisotropic solids subjected to anti-plane shear loading. The problem to be solved is illustrated in the figure below. Two anisotropic elastic solids (with elastic constants such that the solid can sustain anti-plane shear deformations) are bonded across the real axis. The interface contains a crack, which is loaded by distributions of tractions acting on its upper and lower surfaces. Assume that stresses vanish at infinity. The solution is to be generated (using the standard complex variable formulation for anisotropic solids) from two analytic functions, , where is analytic in and is analytic in . We will find that these functions depend only on the generalized shear moduli for the two solids
3.1 Write down the conditions for traction and displacement continuity across the real axis outside the crack, in terms of and
3.2 Express the traction and displacement continuity conditions in terms of functions and , which are analytic in and . Hence, deduce that
are continuous across the real axis outside the crack, and are analytic everywhere.
3.3 Deduce that
provide analytic continuations of and across the real axis
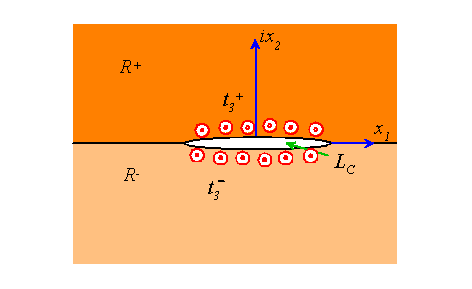
3.4 Show that the traction boundary conditions on the upper and lower faces of the crack may be expressed as
3.5 Deduce that these boundary conditions may be expressed in terms of as
3.6 Finally, deduce the potentials that generate the anti-plane shear solution to a bi-material interface crack between two anisotropic solids subjected to point forces on the crack faces as illustrated below.