 EN224: Linear Elasticity
EN224: Linear Elasticity 
Division of Engineering
8.4 Applications of Minimum Potential Energy II: Bounds and Comparisons
Potential energy methods may also be used to obtain bounds on certain properties of linear elastostatic states. One example is to estimate the stiffness of a solid. We will illustrate this idea by returning to the Saint-Venant torsion problem we discussed in Section 4.
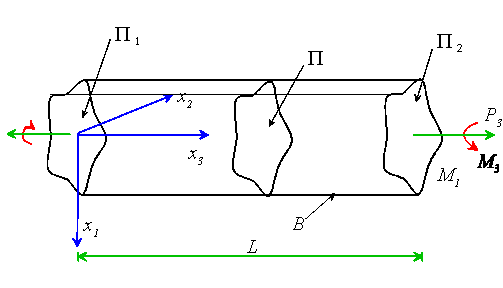
Let ![]() with
with
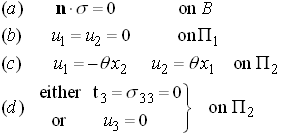
The torsional stiffness of the shaft k, defined such that
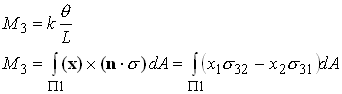
is of particular interest.
We have already found an approximate solution to this problem, of course. We will find an even quicker solution here using energy methods.
Note that we know the actual potential energy is
Now, let v be any other displacement field that satisfies boundary conditions on displacement on the two ends of the bar. We know that
We can readily verify that the boundary terms do not contribute to the potential energy in this case, so that
Hence,
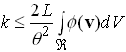
We may now obtain an upper bound on the stiffness by guessing any sensible displacement field. For example, we might assume that plane sections remain plane within the bar, and that each cross section rotates about the x3 axis
The strains and stresses may then be computed, and used to determine the strain energy density. The result is
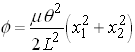
Hence
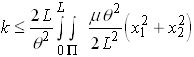
or
We obtained the same result earlier, by solving the Saint-Venant problem. Energy gives us the answer far more easily!
Comparison Theorems
In addition to bounding the stiffness, energy arguments may be used to compare elastostatic states. We will illustrate this idea using two simple examples. Recall the boundary conditions for the torsion problem discussed above were
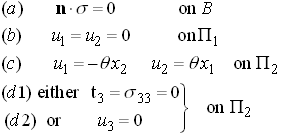
We might ask: which of the two boundary conditions, d1 or d2 will lead to the greatest shaft stiffness?
Observe that all estimates v which are admissible displacement
fields for d2 are also admissible displacement fields for d1.
However, there exist v with ![]() on which are admissible
displacement fields for d1, but are not admissible for d2.
Having a larger set of admissible v suggests (but does not guarantee)
that we might be able to reduce the potential energy. Since the potential
energy leads directly to an upper bound on stiffness here, we conclude
that
on which are admissible
displacement fields for d1, but are not admissible for d2.
Having a larger set of admissible v suggests (but does not guarantee)
that we might be able to reduce the potential energy. Since the potential
energy leads directly to an upper bound on stiffness here, we conclude
that