EN224: Linear Elasticity   

Division of Engineering

 

8.2 The Principles of Stationary and Minimum Potential Energy

 

We now return to linear elastostatics and prove our first energy theorem. Begin by considering a general boundary value problem in the usual way

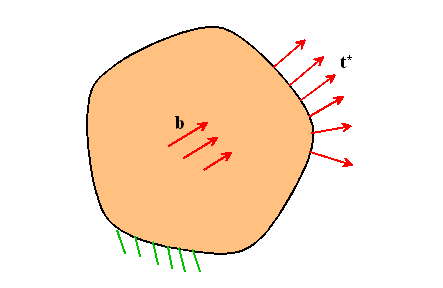
Let with

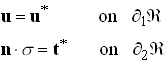
Next, some definitions.

 

Define a kinematically admissible displacement field v to be any displacement field with

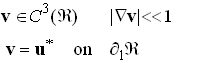
Thus, a kinematically admissible displacement field satisfies any displacement constraints associated with our boundary value problem, and is differentiable enough times that we can compute derivatives of the stress field associated with v.

 

Define the potential energy associated with v to be

where

is the strain energy density associated with v. Note that V is defined only for kinematically admissible v.

 

 

We will proceed to show several important results concerning V, namely

(1) If v is the equilibrium displacement field u, then V is stationary

(2) If V is stationary for some v, then v=u

(3) V is a global minimum at v=u

Begin by stating what we mean by stationary and minimum in the context of a functional of a vector field.

 

Consider a kinematically admissible variation of the displacement field u such that

where is a scalar and is a displacement field satisfying

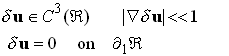
Evidently, with this choice, v is a kinematically admissible field and so we may compute the potential energy associated with v

Switch to index notation to expand this

 

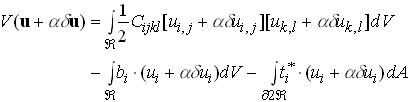
Rearrange

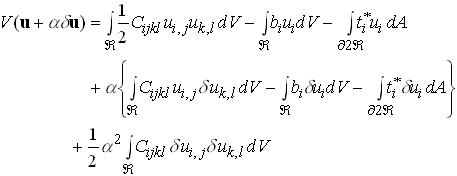
Write this as

In the terminology of the calculus of variations, we refer toand as the first and second variations of V.

 

If for all kinematically admissible variations , then u is a stationary point of V: adding any first order correction to u produces no change in V, to first order.

 

 

If for all, then V (u) is a minimum. Since no other terms appear in the expansion, these two conditions together imply that u is a global minimum of V: no other minima exist.

 

 

The Principle of Stationary Potential Energy

 

V is stationary, i.e.

if and only if with

Proof. We will show first that with implies V is stationary.

 

Assume that

Then, the virtual work equation gives

Hence,

so for all with on

 

Next, we show the converse: that is to say, if V(u) is a stationary point, then u is an equilibrium field satisfying the traction boundary conditions.

 

Start by writing

Integrate the first term on the right hand side by parts and rearrange

where we have made use of the fact that on

Now, since we require for all admissible , we may set

with f=0 on the boundary, which shows that

Finally, let

to see that

 

The principle of minimum potential energy

 

We now go one step further, andtry to show that V(u) is not only a stationary point of V, but is in fact a global minimum. It is evidently sufficient to show that

Where

Actually, we can only show this for displacement boundary value problems. Recall that we require the strain energy density to be positive definite, that is to say

where is symmetric.

The symmetries of C further imply that

Therefore,

but

Thus, for all except for a rigid body motion, in which case .

 

For displacement boundary value problems, , which rules out rigid body motions. In this case, .

For Traction boundary value problems,, with only for a rigid body motion.

For Mixed boundary value problems, for all , as long as the displacement boundary conditions rule out rigid body motions.

 

 

Uniqueness and Existence of Solutions to Static Boundary Value Problems

The results we’ve derived in this section give us a new way to look at uniqueness and existence of solutions to static boundary value problems.

We have shown that V is a minimum if and only if u is an equilibrium field satisfying the boundary conditions. Thus, a solution exists as long as V has a minimum, and the solution is unique as long as the minimum is unique.

Therefore, the solution to displacement boundary value problems always exists and is always unique.

The solution to traction boundary value problems is not unique and may or may not exist.

The solution exists as long as V can be bounded from below: this is the case as long as the external loads do no work in rigid body motions. This is equivalent to saying that the external loads must be in static equilibrium. If the solution exists, it is not unique, since rigid body displacements cause no change in V.