EN224: Linear Elasticity 
Division of Engineering
3.2 Singular solutions for the infinite solid.
Our first 3D boundary value problems will be the simplest: we will derive certain important solutions for an infinite solid. Although one rarely encounters infinite solids in practice, these solutions are useful because one can play clever games with them. For example, we could find a distribution of singular states within an infinite solid that will generate a solution for a bounded region: this is the basis of the boundary element method. We will also find that many important solutions in micromechanics can be derived from the basic singular states, including fields for inclusions, cracks, and dislocations.
We will also use this opportunity to illustrate a few of the techniques that are available for solving boundary value problems.
Concentrated Force in an Infinite Solid (Kelvin State)
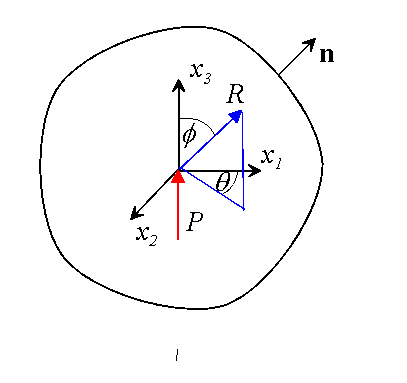
This solution is so important that we will derive it using two different methods, just to be sure!
We begin by stating the boundary value problem carefully. We will see that the strain energy associated with the solution is unbounded, so we have to take special care to ensure that the solution is well posed.
Find
with
where
denotes any region enclosing the origin.
It may be shown that these conditions are necessary and sufficient to determine our solution uniquely; for now, we will assume that this is the case.
Solution obtained by guesswork
We can generate 3D elastostatic states by substituting any harmonic function into the potential representations outlined in the preceding section. If we are lucky, we will find a potential that generates the solution we are interested in.
Examine the list of Boussinesq potentials listed in the preceding section.
Solution A generates solutions with
, while solutions E, F,
G generate solutions with
We would not expect the point force
solution to have either of these characteristics, so it makes sense to
try to generate our solution from representations B, C, or D.
We are looking for a potential function that generates displacements that decay as 1/R. We are looking for a potential that is harmonic everywhere except the origin. We could try as our first guess
Amazingly, this turns out to work: it generates the solution for a point
force acting in the
direction at the origin. We need to check that all
the conditions listed above are satisfied, and compute the value of C.
Evidently, (c) and (d) are both satisfied. To compute the value of C
and to check condition (a), let us evaluate the integral over a spherical
surface centered at the origin. First, compute the stress:
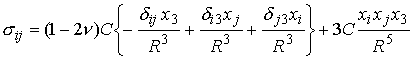
Note 
, whence
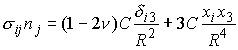
Introduce a spherical polar coordinate system:
to see that
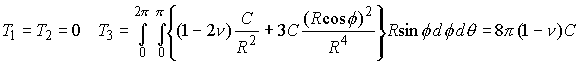
To satisfy 
take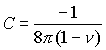
So that the appropriate potential is
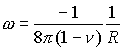
It is straightforward to use the same procedure to show that condition (b) is also satisfied.
Evidently, solutions C and D generate solutions for point forces acting
in the
and
directions. The displacement and stress fields follow
– we will list them shortly.
Fourier Transform derivation of the Kelvin State.
Our prior derivation of the Kelvin state has a number of shortcomings. Firstly, it is not clear what we mean by a `point force.’ Secondly, although we magically found the solution we wanted, we are none the wiser: faced with another problem to solve, we have no idea how to proceed. Finally, how do we know we can represent an arbitrary body force as a distribution of body forces?
We will address these shortcomings next.
Review of Green’s functions
Begin with a brief review of what we mean by a Green’s function for a system of PDEs (or any linear operator). Let us regard the Navier equations:
as a special case of a linear differential operator of the form
where u, b may be scalars, vectors, etc.
Define the Dirac delta
which has the properties
for all f(x) continuous at x=0. There is no function
that has this property, but we can consider a sequence of functions
, increasingly spiky near the origin, that come closer and closer to doing
what we wanted. The symbol effectively stands for a sequence of
approximate deltas. Alternatively, we may interpret (1) as a distribution:
while the function does not exist, the operation (1) is meaningful.
With a shifted origin:
This shows how to represent any function as an integral linear combination of Dirac deltas centered at all possible places:
Now, return to the linear operator L. Suppose we could find a
function
, a function of x which depends parametrically
on 
, that satisfies
then evidently
is a solution of
since
The function is known as the Greens function, or influence function
for the differential operator L. We will see that the Kelvin
state is the Greens function for the Navier equation on an infinite region.
As an example, let us try to find the Greens function for the Poisson equation (a simpler case than the Navier equations). We wish to find a function G satisfying
Observe that the Laplacian is rotation invariant, suggesting that G is likely to be spherically symmetric. Let us assume G=G(r). Integrate over a solid sphere radius r centered at the origin:
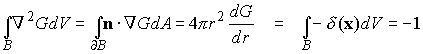
where n is the normal to the sphere, and we have used the divergence theorem. Thus
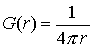
If only all Green’s functions were so easy to find!
Review of Fourier Transforms
We now know that we should look for solutions to the Navier equation of the form
How do we solve this equation? It is not as easy to handle as the Poisson equation, and it would be nice to have a systematic approach to problems of this kind. Fourier transforms are a powerful approach here.
Recall the definition of a Fourier transform. In one dimension:
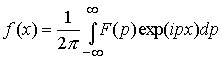
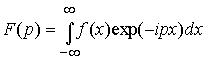
In three dimensions, we have the option of integrating over 3 components, should we choose to do so
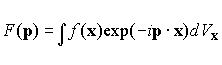
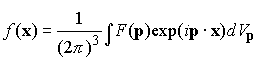
Differentiating the second expression under the integral sign shows that
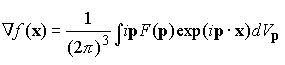
So that
Similarly
We will see shortly that taking Fourier transforms reduces the Navier equation for the infinite solid to a system of algebraic equations, which are easy to solve. To find u, we merely need to invert the transform.
Unfortunately, this is easier said than done. It is usually difficult to evaluate the integrals involved in the inversion. One is usually reduced to hunting through tables of integrals.
Let us collect a small table of transforms. By evaluating the integrals directly, we see that
We can find another transform pair by transforming the equation
whose solution we already know. Clearly
Recall that we already computed G, so
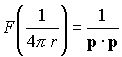
Other results may be derived by differentiating or integrating this one. Furthermore, noting the similarity between the transform and the inversion integrals, we see also that
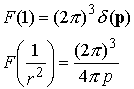
Where
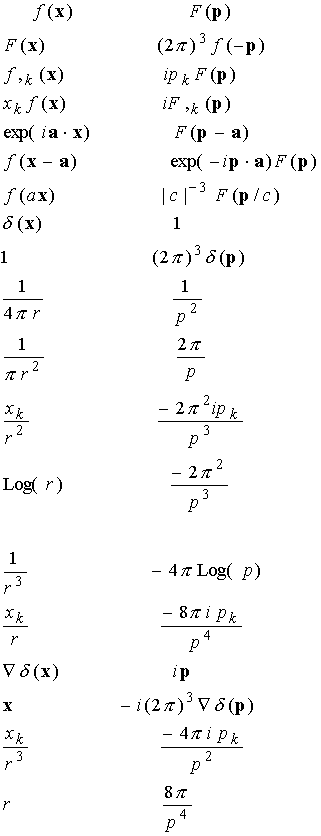
Application to the Navier Equation
Finally, we have all the tools we need to solve the Navier equation formally. Let us assume a homogeneous region (C=constant), so the Navier equation reduces to
We now seek a solution of the form
Let U denote the Fourier transform of u, then
Here,
is known as the `Acoustic tensor.’ It is positive
definite and symmetric, and therefore the equation
is invertible. We can solve for U, and then transform back to find u. Let us apply this to the special case of an isotropic material. Substitute for C to see that
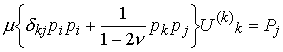
Solving for U:
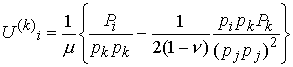
From the table of Fourier transforms listed above (we need to differentiate one of the entries to find the inverse transform of the second term in the parentheses) we see that
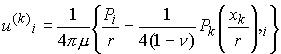
This agrees with our earlier result.
Summary of the Kelvin State
It is straightforward to generalize the solution outlined in the preceding section.
Let
denote the normalized Kelvin state; that is to say, the fields induced
by a unit point force acting in the
at position 
in an infinite
region.
The state is generated by Papkovich-Neuber potentials (See Homework 2)
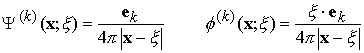
The displacement, strain and stress fields, in Cartesian components, follow as:
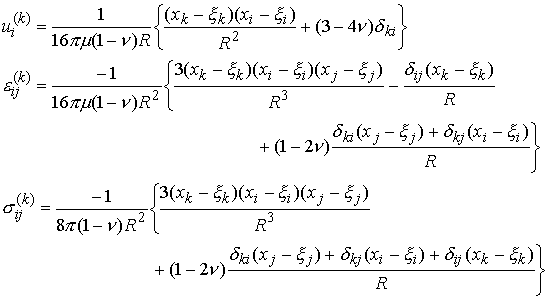
These results allow us to find elastostatic states in an infinite solid
induced by an arbitrary distribution of body force 
. We may regard
an arbitrary body force as a distribution of point forces, so that
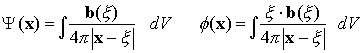
Further Singular Solutions for the Infinite Solid
A whole host of further singular elastostatic states may be derived from the Kelvin state, as follows:
Proposition: Let
denote the normalized Kelvin state. Then define
with
Then
In other words, we can generate further elastostatic states (9 of them in total) by differentiating the Kelvin state. These new states are known as the doublet states.
Proof: follows from linearity and homogeneity of field equations.
We note in passing that the doublet states may be generated from Papkovich-Neuber potentials:
Physical significance of the doublet states
We saw that the Kelvin state could be interpreted as a point force. Do the doublet states have any physical significance? They do, although some of the singular states are hard to visualize.
Let us examine the limiting process that leads to the doublet states
Observe that the Kelvin state has the property
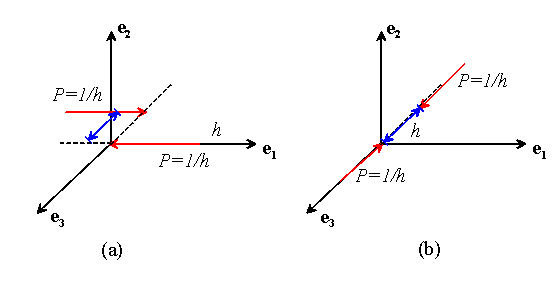
Thus, we can interpret the process of differentiating the Kelvin state with respect to a spatial coordinate as follows
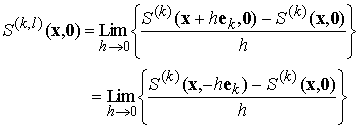
We can visualize the second limit as follows: put a point force of magnitude
-1/h at the origin, and a second point force of magnitude 1/h
at
. Then, let
. This produces either (a) a concentrated moment,
or (b) a force doublet.
What is the use of the doublet states? Well, elastostatic states are always useful, because although they may not solve the problem we are interested in, we may be able to combine or distribute them to get the answer we need. For example, the spherical pressure vessel problem that we laboriously worked out earlier may be found by superposing the solution for a center of compression with a uniform hydrostatic stress. The solution for a center of compression is found from the doublet states as
with summation implied.
The doublet states are also useful because they can be used with the reciprocal theorem to obtain various interesting results. For example, we can now derive the result for the dilatation (or any arbitrary strain component) within a general region.
Recall the reciprocal theorem:
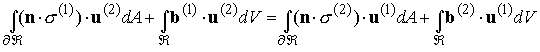
Identify
with the normalized Kelvin state (body force
) and let
be an arbitrary elastostatic state. Then
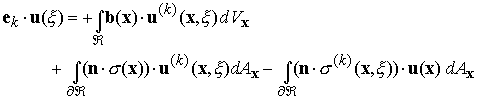
It is important to distinguish between this result and the general solution
for the infinite solid. Note that here we are not distributing point forces
(if we were, we’d be integrating with respect to 
, not x.)
Rather, we put a point force at the position where we want to know
the displacement, and then integrate with respect to the spatial coordinate
x.
Thus, if we know the body force and displacement and traction boundary data, we could compute the displacement field at any arbitrary point. This looks fantastic – almost a general solution, but notice that we almost never know both traction and displacement boundary conditions, we only prescribe one or the other. However, this result is used as the basis for one version of the boundary element method. Note also the similarity between this result and the mean value theorem for the Laplacian.
To get strain components, we merely differentiate, e.g.
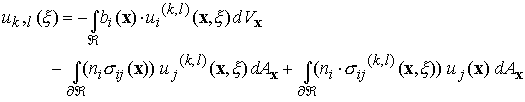
Where we have noted that
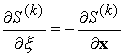
Thus, the doublet states look like Green’s functions for strain components. This result leads to the formula for the dilatation used in the proof of Saint Venant’s principle. The details are left as an exercise. (See Homework 2).