EN224: Linear Elasticity 
EN224: Linear Elasticity
Division of Engineering
2. Theorems of Linear Elasticity
We proceed to prove several useful theorems which follow as a consequence of the structure of the field equations of linear elasticity, and which are useful in interpreting or constructing solutions to boundary value problems.
Begin with the simplest case. Let
be a region, and let
be a time interval. Suppose that
Then
We have followed Sternberg’s notation here: denotes a set
S of displacements, strains and stresses, while
denotes the set of all displacement, strain and stress fields which satisfy the field equations of linear elasticity with body force b, density
and compliance tensor field C on the region
during the time interval
. We will use this notation frequently.
Thus, our theorem states that if
and
satisfy the field equations on the regionw ith body force
and
, respectively, then the linear combination
satisfies the field equations with body force
The proof is trivial: it follows from the linearity and homogeneity of the field equations.
It probably comes as no surprise that solutions to linear elastic boundary and initial value problems are unique. We proceed to show that this is indeed usually the case.
Elastodynamics (Neumann)
Let
be a region with boundary
and let
be a time interval. Suppose
With
And
Then
To prove this, consider
. From the result stated in 2.1, it follows that
with
and
Now, consider the rate of work done on the solid by the external loads associated with S. Evidently
because body forces vanish within the solid, while either velocities or tractions vanish on the boundary of the solid.
From the power identity
Assume that C is such that a strain energy density may be defined (can you remember the conditions on C for this to be the case?) Then
Hence
Integrating
Observe that
so the constant of integration must vanish. Furthermore,
and
are both positive definite,so that
. Finally, we conclude that
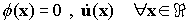
so that the strains, stresses and displacements associated with S must vanish. Thus
, as required.
Note that for elastodynamics, the displacement field is unique even for traction boundary value problems. This is not the case for elastostatic states.
Observe also that our proof has one weakness: we assumed that the volume integrals in the power identity converge. Occasionally, we deal with linear elastic states which have an unbounded strain energy (examples include point forces, and dislocations). Additional constraints are required to ensure that these states are unique.
We also assumed that the boundaries
are known. In contact problems, the contact area is unknown. To ensure that solutions to contact problems are unique, additional constraints are required that allow the contact are to be determined.
Elastostatics
Let
be a region, with boundary
, and let n denote the normal to the boundary. Let
Be two elastostatic states on
, with boundary conditions
Then as long as there are at least three noncolinear points on
Proof:
Begin with the energy identity
(can you show this?)
Then consider the state
. It follows that
with
For this state, the right hand side of the energy identity must vanish, since there is no body force associated with S, and either the displacements or the tractions vanish on the boundary. Since
is always positive or zero, it follows that
everywhere. Consequently
and
.
The displacement field associated with S can at most be an infinitesimal rigid body motion. If there are at least three noncolinear points on
then u=0, and so
Infinite solids
Our proof of uniqueness breaks down for an infinite solid, since it is not clear how one should prescribe boundary conditions at infinity. The simplest way to resolve this difficulty is to require the displacement, strain and stress fields decay at infinity. In particular, it is straightforward to show that the elastostatic state induced by a body force distribution in an infinite solid is unique if the displacements are
as
. The details are left as an exercise.
2.3 The Reciprocal Theorem (Betti)
The reciprocal theorem is a particularly useful tool. It is the basis for the boundary element method; it can be used to obtain information concerning solutions to boundary value problems and can occasionally be used to find the full solution – for example, the reciprocal theorem provides a way to compute fields for arbitrarily shaped dislocation loops in an infinite solid.
Let
be a region with boundary
, let n denote the outward normal to the boundary and let
be two elastostatic states on
. Note that our two states need not satisfy the same boundary conditions. Then
Proof:
Show first that
. Observe that
This proves the last line of the theorem. To prove the rest, note
where we have used the both linear and angular momentum balance to deduce the second line. Similarly
The first two lines of our theorem therefore follow from the last.
Example using the reciprocal theorem
We will show the power of this theorem by using it to solve a problem
Let
be a region with boundary
, and let
With
Note that
must satisfy
to guarantee existence of S.
Find the change in volume of the solid.
The reciprocal theorem can often be used to extract average measures of deformation or stress in an elastic state, and can be applied with good effect here.
Observe that if the displacement field were known, we could compute the volume change from
The trick is to find a reference state
that will turn one of the integrals in the reciprocal theorem into this form. Suppose we take
, and take
to be a uniform hydrostatic tension p, i.e.
The last two terms in the expression for the displacement field represents an arbitrary rigid body motion.
Using the reciprocal theorem
The left hand side reduces to the volume change, while the second two terms in the integrand on the right vanish due to the restrictions on
Hence
2.4 Saint Venant’ s Principle.
Saint-Venant’s principle is often invoked to justify approximate solutions to boundary value problems in linear elasticity. For example, when we solve problems involving bending or axial deformation of slender beams and rods in elementary strength of materials courses, we do not prescribe loads in any detail. Instead, we specify the resultant forces acting on the ends of a rod, or the magnitudes of point forces acting on a beam. We rely on Saint Venant’s principle to justify this approach. In this context, the principle states the following. Suppose we calculate the fields in a slender rod due to two different (self equilibrating) traction distributions which act on the ends of the rod. If the two traction distributions exert the same resultant force and moment on the rod, then the difference between the two states at a point distant from the ends is an order of magnitude smaller than either state.
Saint-Venant himself limited his principle to the problem of extension, torsion and flexure of prismatic and cylindrical bodies. There have been various attempts to generalize the principle, for example:
Boussinesq: An equilibrated system of external forces applied to an elastic body, all of the points of application lying within a given sphere, produces deformations of negligible magnitude at distances from the sphere which are sufficiently large compared to its radius.
Love: According to this principle, the strains that are produced in a body by the application, to a small part of its surface, of a system of forces statically equivalent to zero force and zero couple, are of negligible magnitude at distances which are large compared with the linear dimensions of the part.
Sternberg gives a more satisfactory statement of the principle:
If the forces acting on an elastic body are confined to several distinct
portions of its surface, each lying within a sphere of radius
, then the stresses and strains at a fixed
interior point of the body are of a smaller order of magnitude in
as 
when
the forces on each portion are in equilibrium than when they are not.
Sternberg provided a rigorous proof of this version of the principle, which we outline below. Before doing so, we will illustrate the principle with a two examples:
Surface loaded half-space.
Closed form expressions are known for the fields induced by many axisymmetric traction distributions acting on the surface of a half-space. For example, the fields down the symmetry axis due to a uniform normal pressure acting on a circular region of radius a are:
Where P is the resultant force acting on the loaded region. Similarly, the stresses due to a Hertz pressure
are
Expand these in a/z and you will find that to leading order in a/z both expressions are identical. Indeed, the leading order term is the stress induced by a point force acting at the origin. Far from the loaded region, the two traction distributions induce the same stresses, because the resultant force acting on the loaded region is identical.
To see how this relates to Sternberg’s statement of Saint Venant’s theorem, note that we could construct a self-equilibrated traction distribution acting on the region r<a by subtracting one of the states listed above from the other. Distant from the loaded region, we find that the stresses induced by this loading are of a smaller order of magnitude than the stresses induced by either traction distribution listed above.
For our second example, consider an end loaded semi-infinite strip.
This is a problem that has received considerable attention, because it provides some insight into Saint Venant’s principle.
It is possible to generate a general class of solutions which correspond to self equilibrating traction distributions acting on the end of the strip. The stresses are generated from and Airy stress function
which has the form
Where
is a complex number that satisfies either
or
A closed form solution for g(y) is available, but the details need not concern us here.
The stresses in the strip evidently decay exponentially. The largest real part of
is found numerically to be 7.4/H. This suggests that the stresses due to a self-equilibrating distribution of traction decays to about 2% of the value at the end, within a distance H /2 of the end.
These examples serve to illustrate Saint Venant’ s principle. We proceed to prove Sternberg’s version of the principle
Let
be a region with boundary
. Let
be m non intersecting closed subregions of
which lie within the neighborhoods of m distinct points
.
Suppose that the solid is subjected to a self-equilibrating traction distribution
on
and suppose t vanishes on
with the exception of the subregions
We will consider the behavior of the stress state at a point within the solid as the size of the loaded regions approaches zero.
To make this precise, consider a one-parameter family of closed subregions
such that
lies within a sphere of radius
centered at
, as illustrated in the figure.
Let
satisfying
and assume that
vanishes on
We now consider the behavior of
as
. To keep things simple, we will consider the behavior of the dilatation
To do this, we need a way to find S for an arbitrary traction distribution on
Fortunately, although we can’t find S, we can say enough about it to be able to prove our theorem. Later, we will show how to construct a Greens function for an arbitrary region. For now, we will state the result:
The dilatation at a point x within
Where
and the function
may be (formally) constructed as follows
where
and
is the displacement field associated with an elastostatic state
with
Here, C denotes the tensor of elastic moduli.
This result is important, because allows us to find the dilatation at any point in our solid due to any arbitrary surface loading, by solving a single boundary value problem for
. We will see later that this approach can give all stress, strain and displacement fields in our solid, not just the dilatation. As you have probably guessed, the result is proved by applying the reciprocal theorem.
For our purposes, we do not actually need to find
Now, returning to our problem, we can evidently compute the dilatation at some point as follows
Consider the contribution to
due to one of the subregions. Introduce a curvilinear coordinate system
on
and assume that
It is also convenient to choose the coordinate system so that
, where
is the position vector of the point
Now, expand
Now define
and consider the behavior as
Recall the meaning of the concept of an `order of magnitude:’ If
Recall that we assumed that t are bounded as
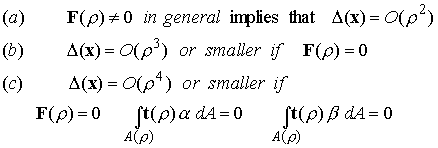
The conditions
imply M=0, but the converse is not true in general.
This proves Sternberg’s statement of Saint Venant’s principle. Exceptions to (a) are possible: one occasionally finds points in a solid where the dilatation happens to vanish, for example. We will see an example later.
Some observations:
Concentrated forces: It is straightforward to extend the argument to account for concentrated forces. In this case, we assume that F tends to a finite limit as
with
, respectively.
