EN224: Linear Elasticity    

Division of Engineering

 

8. Energy Theorems and Applications

As always, energy methods provide a powerful way of approaching problems in linear elasticity. Energy methods can be used to obtain approximate solutions to boundary value problems. They can often be used to obtain rigorous bounds on the stiffness of an elastic structure or solid. Energy methods also provide new insight into general issues concerning uniqueness and existence of solutions to boundary value problems. Finally, several numerical techniques for solving elastic boundary value problems are based on energy principles.

In this section we will prove the most important energy theorems in linear elasticity and discuss some of their applications.

 

8.1 The Principle of Virtual Work

The principle of virtual work has nothing to do with linear elasticity, but it is convenient to start thinking about energy methods by reviewing a principle that you’ve probably seen before.

Let be a state of stress satisfying

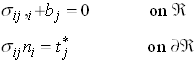
Furthermore, let be a displacement field on and define

Then

This is known as the Virtual Work equation.

 

Proof: It has been suggested that every result in solid mechanics is obtained by applying the divergence theorem. So, observe that

Hence

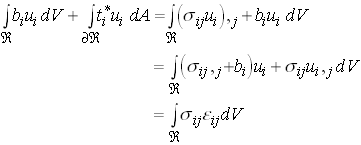
Where we have used the equilibrium equations (including the symmetry of stress) to obtain the last line.

 

The virtual work equation is not particularly interesting. The converse is much more exciting:

Let be a symmetric stress field satisfying

for all displacement and strain fields with

Then

 

 

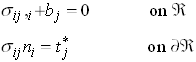
Proof: For sufficiently smooth , we may write

Then, use the divergence theorem to express the virtual work equation as

Recall that we required the virtual work equation to be satisfied for all displacement fields, so in particular, we may choose

with

Then

Next, suppose that the displacement field satisfies

Then

This completes our proof.

 

Why is this useful? Well, it gives us a new way to think about equilibrium in a deformable solid. For example, it allows us to extend our ideas about equilibrium to stress fields which have jump discontinuities.

 

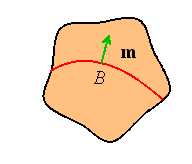
Let be a region, and suppose thathas a jump discontinuity across some surface B.

 

We now define an equilibrium state of stress to be one that satisfies the virtual work equation for all displacement fields. It follows that

Hence