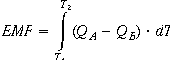VISUAL DISPLAYS bulb & liq xtal
bimetallic switch, on-off for control
NITINOL as a temperature sensitive controller...JDH
platinum resistance thermometers
thermocouples
thermistors
"solid state" sensors
temperature actuators
temperature sensitive nerve cells: peripheral and central. Skin
and Hypothalamus.
speed of response; spatial accuracy.
§1 / 1 Temperature dependence of materials
Free valence band electrons in a heated metal find their mean free path reduced, thus resistance increases. When they're given more energy by heat, outer shell electrons in nonmetals (semiconductors and insulators) move into the free valence band and thereby lower the resistance of nonmetals.
But what do you make of the current voltage relationship for a semiconductor diode?
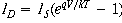
Yike! it looks like when temperature goes up, current goes
down, implying an increase in resistance! What can rescue us?
IS , reverse bias current, depends on temperature too! IS(T). For every 5 degC increase, IS
doubles; it goes up much faster than the other term goes down!
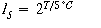
§1 / 2 Platinum resistance thermometer
From Derenzo, page 157:
"Platinum is a noble metal that can withstand high temperature and harsh chemicals with
good stability." A platinum wire is carefully cut to have exactly 100W of resistance at 0°C
It's change in resistance is given by
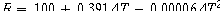
Thus a 10°C change in temperature results in about 4 ohms increase in resistance.
A platinum strip can be a temperature standard.
§1 / 3 Bimetallic strip
Can be wound into a helix or a coil for more angular deflection.
Derenzo has a table of thermal expansion coefficients for different metals and alloys:
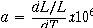
Notice STRAIN in the numerator.
bimetallic strips are used in many low-cost rugged temperature sensors (meat
thermometers, etc). They can be used in on-off electrical circuits when they complete or
break a circuit
Metals are good for this application because they have large thermal expansion
coefficients, then can be joined together easily, they can flex without breaking, and they can
conduct electrical currents.
Question: Does the circuit above have hysteresis? Maybe it has "thermal inertial"...
Bimetallic strip in thermostats?
nitinol DEMO, of a mechanical temperature effect, used for
vena cava clot filters.
§1 / 4 Thermistors
See Boctor & Ryff preprint, Chpt 10, p. 26 ff, on thermistors, and Derenzo, p. 165 ff
Boltzmann relationship states that the number of electrons in the conduction band
depends on temperature with exp(E/kT) where E is band gap energy for the material. As T
increases, the Boltzmann factor increases. Thermistors are basically sintered
semiconductor material. not polarized, not a diode junction.
we will use, for Lab 2, negative temperature coefficient NTC thermistors.
Resistance of the thermistor, RTh, at temperature T, is calculated by
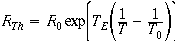
where R0 , T0 , are reference resistance and temperature, and TE is a property of the
semiconductor material; Boctor and Ryff suggest a nominal value of 4000 deg K, where the
other T's in the formula are also converted to deg K. If ambient temperature is greater than
reference temperature then the exponent is negative and the factor multiplying R0 is less
than one.
§1 / 4 / 1 Self heating
If you know R0 , T0 , TE , and T, the ambient temperature then you can use the above formula
to calculate the expected thermistor resistance RTh . Notice nowhere in the formula above
is any consideration given to the circuit the thermistor is in. Because current must flow
through a resistance for the thermistor to provide a measurable voltage, invariably power
will be dissipated and heat generated. The heat can change temperature. Place a thermistor
in a bridge circuit to work out the problem of self heating.
The following power equation 
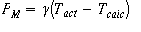
that says power dissipated by
the thermistor is equal to the temperature difference of actual versus calculated, times a
conversion factor. The equation can be solved for 
**
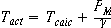
where g is the dissipation constant and Tcalc is the zero power calculated temperature
(apparent temperature) and Tact is the actual temperature being measured. 1.7 mW/°C is
typical for standard thermistors in air. Power is 
. In fact, Tact, is the steady state value of
self heating temperature. The above equation (**) is taken from Derenzo.
More properly, time must elapse for temperature to change from calculated to actual.
The following first order rate equation balances energy transfer (J/s = W = power)
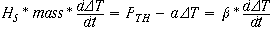
, and expresses the dynamics of the
situation. DT = Tnow - Tcalc. When DT is zero, at the time t = 0, Tnow = Tcalc, then long after the
time constant has been exceeded, the (**) steady state equation holds, with Tnow = Tact.
HS is the specific heat of the material in question, and has the units of Joules/(deg-gm); for example the specific heat of water is 1 cal = 4.18 J and is the energy required to heat one gm of water one degree C. Each term in the equation above has units of Joules/sec = watts. The equation has a decaying exponential solution with a time constant of b/a; which is 1/gamma in the original formulation.
Recall from thermodynamics that convective heat transfer is described by
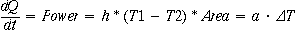
, where h, with units of
Joules/deg-cm2, is the convective transfer coefficient; h is a property of the two-material
surface exchanging heat (thermistor and air in this case).
Dynamic Example. See Simulink JDD file "selfheat" for a demo of selfheating that accounts for increasing T as a function of time. The first order diff. equ is solved with an integrator; the time constant of change is 1/g. Gamma depends on the mass, surface area, material, and convective surface: If g is 2 mW/deg C, then the time constant is about 500 sec. The example takes account of the mass, the area and the specific heat (0.5 J/deg-gm) of carbon graphite, for the resistor. For the multiplier of dT/dt, Hs*mas, 0.5 J/(deg-gm) * 2 gm = 1 ! Note also that d DT/dt = dT/dt.
Steady State Example. Suppose a 4 volt drop is across a 2000 W thermistor; suppose that results in a calculated temperature of 20 °C. In fact you'll use the temperature to calculate the resistance and thence the voltage. Find that P = V2 / R = 8 mW. Divide P by g to see 8/1.7 = 4.7 deg. so actual junction temperature Tact is about 24.7°C , due to self-heating.
Of course you can find the real ambient temperature by a calibration procedure instead of a calculation! In the case of Lab 2, that means you need to worry about placement of the calibration probe, the thermocouple.
Question: which is more likely to have significant self-heating: a 300 ohm thermistor, or a 100K ohm thermistor?
DEMO: a 300 ohm thermistor in series with a 100 ohm resistor connected to a 9 v battery, measure voltage across the thermistor after power applied; watch the voltage decrease by about 20% over a minute or so!
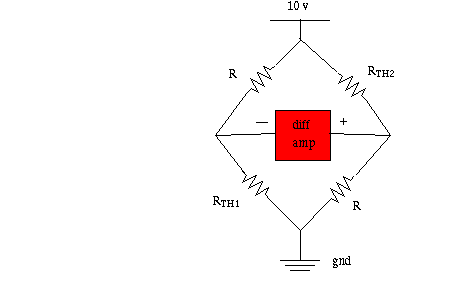
§1 / 4 / 2 Thermistor in a bridge
Placement of thermistor in a bridge: In the bridge, the thermistor has other resistance in
parallel with it, and one in series; these may improve linearity. On which leg of a
Wheatstone bridge should you place the thermistor to get a positive slope to the
voltage-temperature curve? (one choice: upper right, with right side of bridge positive.)
The thermistor in the bridge will give a nearly zero voltage at reference, so that a sensitive scale of a
voltmeter can be used. What happens at bridge output if you place a second thermistor in the
opposite leg of the bridge?
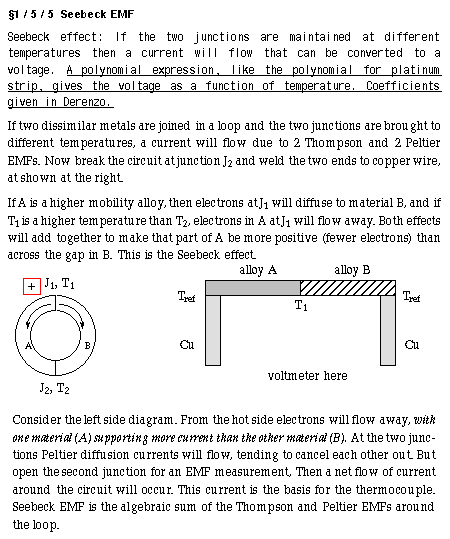
§1 / 5 Thermocouples
Review of Boctor & Ryff, page 92: 4 thermoelectric phenomenon: & See Derenzo,
page 150 ff. & Curtis D. Johnson, 5th edition, pages 168 ff.
Joule effect,
Thompson effect,
Peltier effect: half cell voltage
Seebeck effect.
See Fig. 4.7 of CD Johnson book .
§1 / 5 / 1 Joule effect
§1 / 5 / 2 Thomson EMF
Heat up one end of a metal bar and electrons will head for the cool end, creating a charge separation (reminds one a little of piezoelectric material). You can't measure a voltage with a meter but if heated wire is put across terminals of a battery (cool end on negative terminal) heat will be converted to electrical energy.
If a junction is heated, then the
the voltage developed is 
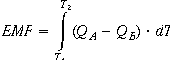
where QA and QB are the thermal transport constants of the two metals. T1 and T2 are the
two junction temperatures. QA and QB are material properties nearly independent of
temperature, so in practice, EMF = a (T2 - T1)
§1 / 5 / 3 EMF of dissimilar metals junction
Connect together by welding two dissimilar metals and the electrons in the higher mobility metal will diffuse to the low mobility side until an opposing voltage stops further charge separation. We'll see quantitative development of this theme in lectures on metal-to-skin electrodes. Notice that in the case of dissimilar metals the "concentration" of electrons is the same on both sides, the only difference is mobility of the electrons.
§1 / 5 / 4 Peltier cooling
If electrons are forced from the low mobility to the high mobility side, the effect is like an expanding gas and the junction will be cooled. [Derenzo, page 160: see figure ]. Peltier effect: If electrons are pumped from the low mobility side to the high mobility side then they will absorb heat as they cross the junction, and the junction will be cooled. As the circuit is completed through two junctions of dissimilar metal, then one of the junctions will heat up and the other will cool below ambient temperature. A Peltier cooler has biomedical applications in locally cooling tissue. It can be the basis for some humidity measuring devices.
DEMO! Peltier junctions: go to website
http://www.tellurex.com
for more information on the devices we demonstrate in EN123. See the series
electrical connection of parallel semiconductor junctions.
You see a thermoelectric structure capable of handling 4 amps at 16 v.
Bismith telluride is the semiconductor involved.
Insert a current source in a Seebeck loop (see below) and one junction will be cooled, the other warmed up! requires a lot of current...used for freezing tissue locally in biomedical applications.
Two dissimilar metals connected together, with different electron mobilities (material property), create a "half cell battery." As soon as the metals make contact higher mobility electrons will diffuse across the junction. Peltier EMF is the potential that develops. (Can't measure it directly, same problem as in chem, where you can't directly measure a half cell voltage. Need to combine it with a standard) However, resistances are different in the two directions, like a diode.)
Eventually the extra electrons set up an electric field which opposes more diffusion. We'll
see this diffusion/field effect again, in biopotentials, where Jdiff + Jdrift = 0
across the junction.
As shown in Derenzo, the rate of heat loss, in terms of current flow in an object with a cold
surface is given by: (should the surface area be taken into account?)
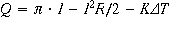
Can detect a change in current if heated junction is part of a complete circuit. (Derenzo)
Maintaining reference. The copper junctions need to be kept at a constant temperature for an accurate reading. Can be done by long wiring to remote reference, in an industrial/lab setting, where 0 deg C is the standard. How is it done with the Fluke 52? Compromise, near room temperature, measured internally with a thermistor. What happens to initial output if the Fluke is kept in the freezer for an hour?
Thermocouple materials: Constantan is a nickel alloy. Cooper-Nickel is a
standard thermocouple combination. Constatan, chrormel and alumel are
trademarked names for thermocouple junctions.
Thermocouple tables give output EMF for a given reference and a given measured
temperature, for each type of junction. Voltages are typically less than 100
mV. See Derenzo. Sensitivities range from 7.6 to 67.9 microvolts/deg C.
Advantages: Can be used at higher temperatures than thermistors. No self heating.
thermomopile: thermocouples in series.
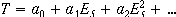
Polynomials in thermocouple measurements.
getting down to 10-6 degree centigrade for muscle heat experiments of A.V. Hill!
Polynomials in thermocouple measurements. getting down to 10 exp -6 degree centigrade for muscle experiments.
Summary List
* How temperature affects materials
how resistance is affected in metals and semiconductors.
Platinum strip
* Temperature dependence of semiconductor diode. IS(T)
* Bimetallic strips
* Thermistors: semiconductors with great temperature dependence of resistance
* Thermocouples: temperature dependent voltage between dissimilar metals.
* Demos: Peltier effect; self heating in a thermistor.
OLD NOTES: INCREASE MERCURY COLUMN HEIGHT AND USE AS A SWITCH
Boltzmann formula for electrons in conduction band
Later: HEATERS AND CURRENT GAIN