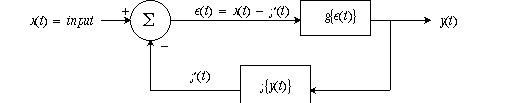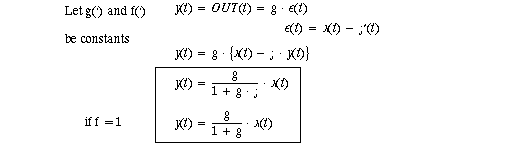§ 1 Feedback in Instrumentation Systems
----------------
§ 1 / 1 The varieties of feedback experience
As engineers we want to move beyond a hand-waving verbal account of feedback, to
a mathematical description which will allow us to model and predict various actions of
negative feedback controllers. This lecture introduces the context of feedback and tells you
about the virtues of feedback in any system. You'll learn how feedback can stabilize, speed
up and regulate a system. Part of what you'll learn is terminology: feedback vs feedforward,
negative vs positive feedback, discrete vs continuous and linear vs non-linear feedback.
A SIMULINK demo may be given for a non-linear feedback system. Use
Mathworks program SIMULINK to build dynamic systems with feedback.
Consider dynamics of delay and integration. Simulink is like LabVIEW:
A graphic-based
Some knowledge of Laplace transforms is helpful. You have seen Laplace transforms in
AM33 and EN52.
Feedback means sending a copy of an output signal back to an input summation part of
the system, where it can influence the system components which helped form it in the first
place. If this definition sounds circular, it is! It may remind you of recursion in programming.
The copy of output sent as feedback may be attenuated or amplified; it may even be
reversed in sign. In any physical system the feedback path is inevitably associated with
some delay. The dynamics of that delay can create some of the most useful or destabilizing
effects. In the diagram below a summation unit adds external input to output transformed
through a feedback circuit. The effect of feedback may be positive or negative at the
smmat.
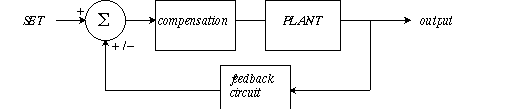
The summation point can be an op amp configured as a summation amplifier. The forward pathway has two parts: The Plant is the apparatus itself--muscle, reactor vessel, oven, motor, etc.--generally the Plant is not amenable to adjustment. Compensation is where your design skills come in. Compensation may have gain, may have a controller for the plant, a filter for the output of the comparator summation unit. The feeback circuit is the SENSOR, and it may translate a physical parameter such as temperature or air flow into a voltage.
Negative feedback is useful in various situations where an output should be maintained at
a desired level in spite of "load" disturbances. In physiology, where negative feedback is
called homeostasis, it helps regulate blood pressure, blood sugar level, etc. In EN123 you
will build a feedback control system for regulating air flow from a fan.
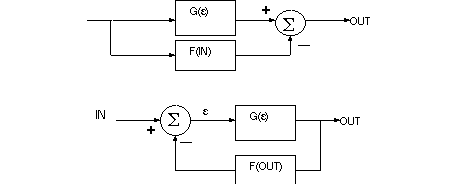
§ 1 / 2 Closed loop gain calculation
Shown below are feed-forward and feedback configurations, with subtractive
comparisons at the summation units.
Now we develop the basic feedback equation, using algebra. The compensation and plant
have been combined into one forward path unit, G. Assume a system output y(t) is
intended to match a goal x(t), shown in the figure below. Without feedback y(t) = g(x(t)),
where g is called gain and is a function-anything from multiplication by a constant to a
differential equation. With negative feedback an error = x-f' is amplified by gain g until the
negative feedback reduces error to an acceptable level. The feedback signal is formed as
the product of y·f, where f is the feedback gain and f' is the feedback signal presented to the
summation amplifier on the left.
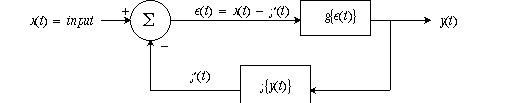
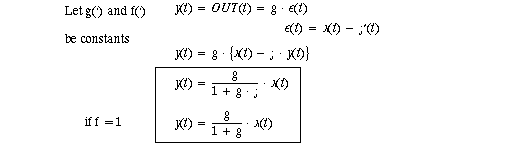
It's negative feedback because of the subtraction of f from goal x.
Note that closed loop gain is lower than open loop gain. In fact if f=1, closed loop gain is always less than 1! This reduction in gain had better be good for something!
§ 1 / 3 Virtues of negative feedback
§ 1 / 3 / 1 Reduce sensitivity to internal parameter changes
Suppose g = 100 in the system above. Then the close loop gain is
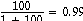
Now suppose g changes by a factor of 2, to 200. The close loop gain is still about 0.99.
Negative feedback reduces sensitivity of the system to changes in internal parameters. In
this case the only internal parameter we have is open-loop gain. What could make the
system sensitive to gain changes? If the gain is too low, less than 10 for example. In general,
a high open loop gain is desired.
§ 1 / 3 / 2 Reduce sensitivity to external load changes
Let a variable load affect the output, as shown below:
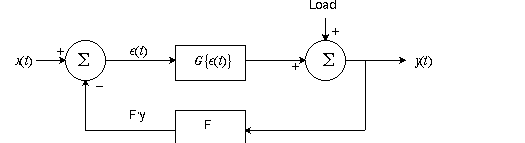
Now

Let F = 1.
Isolating y on one side of the equation,
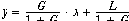
If L = 0 then the same G/(1+G) factor results. Even if L � 0, the effect of load on the output is
reduced by 1/(1+G) !! Thus negative feedback systems can have reduced sensitivity to
external load changes. As an example of external load, consider a beaker held up by the
neuromuscular system of the arm; the aim is to hold the beaker at a constant position in
spite of liquid being poured in.
Example of plant and load dynamics: Suppose the plant is a LP filter (leaky integrator)
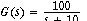
, a gain-of-10 filter for s= jw << 10. Now suppose the load changes
suddenly, at t=0, from 0 to 2: that would be a step of magnitude 2: L(t) = 2*1(t) where 1(t) is
the step function. The Laplace transform of the step is 1/s, thus
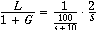
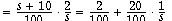
and the inverse Laplace transform of
the right side is
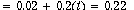
for t > 0, which is about 2/10, the steady state
answer.
§ 1 / 3 / 3 Increased speed of response
Now to dynamics. Consider the negative feedback system shown below. Forward path
and feedback are represented by Laplace transforms, so multiplication of transfer
functions can take the place of time-domain convolution integrals. Let G(s) be
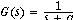
, a first-order system. [What time function is this a transform of? What
differential equation does the Laplace transform represent? A leaky integrator, or first order
LP filter.] Let feedback be F(s)=k, where k is attenuation: 0 � k < 1.

If F(s) = 1 then the open loop response of the system is Y(s) = In(s) · G(s).
If In(s)=1 (impulse function) then
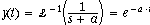
a decaying exponential with time constant 1/a. The larger a is, the faster the system
decays. And decay to zero is what we want, when the input is an impulse. The impulse is a
brief disturbance, and we want the system to return to its zero state as soon as possible.
After t=0 input is zero, and we want y(t) to track the input. Now consider the closed loop.
Substitute G(s) in the formula G/(1+G),
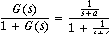
which we can do because we are in the frequency domain. If we were in the time domain,
convolution would be called for.
The formula simplifies to
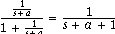
which has inverse Laplace transform
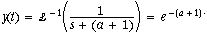
Compared to the open loop form the time constant 1/(a+1) is smaller, so the system
decays to zero faster. Suppose F>1 then the time constant will be even smaller than for
F=1. Bottom line: Negative feedback can speed up the response of a dynamic system.
§ 1 / 3 / 4 Improve stability
Now consider an unstable dynamic system:

Give the open loop block a Laplace transform with a negative time constant and set
feedback F = 0. The inverse Laplace transform is
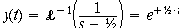
The exponential is positive. The system is unstable. It's impulse response grows
exponentially. Now consider what happens if negative feedback is put in place.
Let F=1.
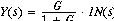
Substituting
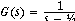
in the formula we obtain

Let IN(s) be 1, for the input to be an impulse function.
now
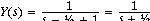
which has a time domain form of
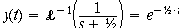
A stable form with a decaying exponential. What's the time constant?
Bottom line here: Negative feedback can stabilize a system.
Add that to the list of negative feedback virtues.
Notice that in the dynamic examples given, we haven't been worried about large open loop
gain, but certainly large open loop gain can be a feature of dynamic systems.
The next example has unity open loop gain.
§ 1 / 4 Two more examples: Inverse systems and positive feedback
§ 1 / 4 / 1 Inverse systems in feedback
Place the dynamic element in the feedback path,
while maintaining a high open loop gain A :
Let
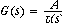
where p(s), as you may recall from EN52, is a polynomial for the poles of G(s).
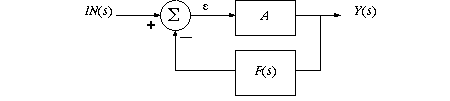
Applying the feedback formula
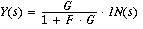
to this arrangement, while
letting IN(s) be 1, for the impulse input, we find,
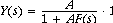
As usual, let's assume A is a huge number,
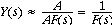
Voila: The output is the inverse of the feedback path. Sometimes we seek the inverse of a
system in order to "cancel" some effect or other. This is the idea behind a gyrator in filter
design: turn a capacitor into an inductor for the sake of filter sharpness.
§ 1 / 4 / 2 Increasing the time constant with positive feedback
Look at a dynamic system with positive feedback k less than 1:
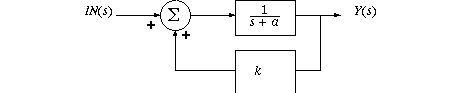
Apply the feedback formula to find
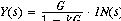
Let
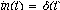
and we have
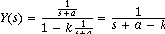
OK, let's say k < a. If so, then a-k is a positive number smaller than a.
And the time constant of the system,
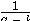
is correspondingly larger.
Positive feedback can be used to "plug up" a leaky integator, such as a resistor and
capacitor in parallel.
§ 1 / 5 Positive feedback producing an oscillator
For now consider the the effect of delay in the one-inverter-with-feedback:

OUT becomes IN almost instantly, in "rise time" s, but IN must wait a longer transport time D before it starts to change to the new value of IN. Assume D >> s. The result is the following "timing diagram" for input and output waveforms. Thinking about what causes what can send you around in circles, so start by considering that the circuit has just been turned on, and IN is zero. As soon as power is applied, OUT goes (with rise-time s) to HI, but a change of IN to HI must wait for delay D to expire.
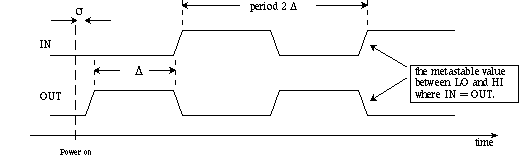
An oscillation, with period 2·(D+s), results.
[If s > D, then the metastable condition can last "a long time"; such may be the case with various IC inverters.]
(To be more careful in this analysis of feedback we must specify the thresholds
qH and qL
at which the inverter snaps from one binary value to another.
Assume for now that
OUT will snap up if IN < 1 volt = qL, and
OUT will snap down if IN > 4 volts = qH .
§ 1 / 6 Delay in feedback
The Laplace transform of pure delay is:
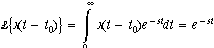
An example: The signal going up from a spindle to a motoneuron in a feedback loop is not
just slowed down by an integration process, it is absolutely delayed by finite (and slow)
conduction speed. In engineering terms such delay is called transport delay. It's
commonly seen is chemical engineering systems where fluid to be measured is
transported down a pipe until it arrives at a sensor. How can we handle pure delay in terms
of Laplace transforms? The Laplace transform of pure delay is
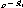
where t0 is the duration
of the transport delay. The exponential can be approximated by the Maclaurin series,
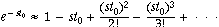
or by the Pade approx:
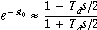
which I will try to demonstrate with SIMULINK!
§ 1 / 7 Proportional, integral, derivative compensation
Control engineers call it PID. So far we have considered mainly proportional
compensation, where the error signal is multiplied by some proportional factor, KP. We will
look briefly at the effects of PID compensation. For example, integral feedback is capable
of driving the error of a system to zero, not just to some small value. Follow the
development in Wolovich's book, pages 271-286, handed out.
Studio session: It is possible, but awkward, to use LabVIEW to design feedback systems
and analyze them. A more efficient approach is SIMULINK modeling. On the sunserver
network you will use SIMULINK under MATLAB to create the system described in the
Wolovich chapter.
Printing from the SIMULINK screen: In the Matlab command window type >> print -s to
print the top window. If the Graph won't print go to the UNIX command line and call up % xv.
In xv go to GRAB, hide the XV window, give a delay of 2 sec, then grab the scope by the top
bar, so the trace doesn't disappear. Then use the PRINT menu to get hardcopy.
OR, try % xwd | xpr | lpr and click on the window you want to print!
§ 1 / 8 Regulation of air flow
Show OUT = BIAS + Reg(s) as output air flow.
(actually may be non-linear relationship between voltage and flow...)
Reg(s) is the output of E(s)M(s) where E is the error,
E = Set - F(s)OUT
and M(s) is the fan characteristic
Set is the desired airflow
OUT(s) goes to T(s) the tach and perhaps gain or C(s), compensation.
Gain may be needed in the "open loop"
We end up with an equation
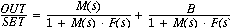
(that demonstrates regulation of B type noise...)
we would like OUT to equal SET
§ 1 / 9 Reading with text
W. A. Wolovich Automatic Control Systems, Saunders, Phila (1993), "PID Compensation,"
pages 271-286.
Curtis D. Johnson, Process Control Instrumentation Technology 5th Edition, Prentice-Hall
(1993).
§ 1 / 10 Other Reading
Clare D. McGillem & G.R. Cooper, chapter 5, §15, "Feedback systems,"
pages 270-283, in Continuous and Discrete Signal and System Analysis, 3rd Edition,
Holt-Rinehart and Winston (1991).
V. S. Vaidhyanathan, Regulation and Control Mechanisms in Biological Systems,
Prentice-Hall (1993).
Oppenheim & Willsky, chapter 11 (first 2 §'s) pages 685-701 in Signals and Systems,
Prentice-Hall (1983). O&W was the EN157 book a few years ago.
§ 1 / 11 Summary
* G/(1+G) NOTE LOWERED GAIN
* G/(1+FG) If FG>>1 then an inverse system F-1 is created.
* Virtues of negative feedback
insensitivity to parameter or load changes
increased speed
better stability
* Frequency response: What spindle input does in the cord
* Delay & stability & non-linear/time varying
* PID = proportional/derivative/differential