"At a soirée of the Royal Society conducted by Hill in 1952 two subjects mounted a specially built tandem stationary bicycle. While one subject pedaled the other subject resisted him through directly coupled pedals. At a speed of 35 revolutions per minute, the subject pedaling forwards used 3.7 times as much oxygen as the one pedaling backwards. It was demonstrated that a small woman, pedaling backwards, could rapidly exhaust a large man pedaling forwards against her resistance. Since oxygen consumption and heat production are closely tied, the muscles of the woman were presumably generating far less heat, even though the coupling of the pedals guarantees that the forces and displacements experienced by the woman's feet were the same as those for the man's." Thomas A. McMahon, from chapter 2 of Muscles, Reflexes and Locomotion, Princeton Univ Press (1984).

Background:
The lecture notes tell you about Hill's equation for muscle velocity-tension

with the figure below from McMahon's Muscles Reflexes and Locomotion

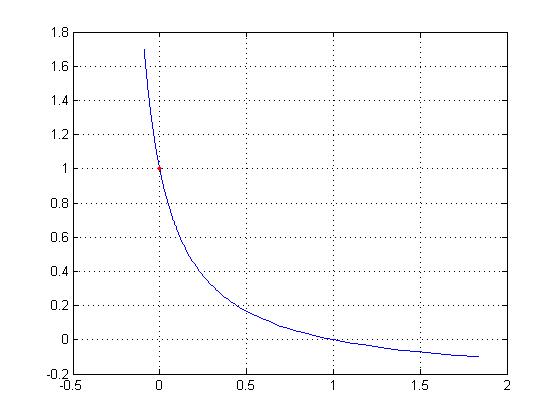
note the greater tension/fiber for negative velocity. The graph has been normalized

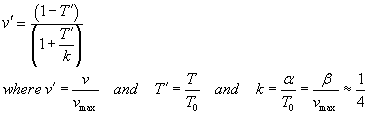
where we use 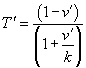in the Matlab code described below, and you have control of constant k.
Note that α and β have the units of tension and velocity, respectively.

Muscle details:
1. Recruitment. To increase tension (or velocity of contraction) muscle fibers are recruited, from the weakest fibers (with the most endurance) up to the strongest fibers, which are most easily fatigued. Yes is it true that individual fibers can be stimulated at increasing rates by their motoneuron axons, up to tetanus tension, but to once one fiber is pulling to the max, another fiber is recruited as necessary. In the simulation below we have it that the "strong biker" has 100 fibers involved in pedaling, with the maximum tension of the fibers from 1 to 100 force units. In exercising the simulation (Tandem04.m) you choose the number of "weak biker" fibers, an integer less than 100.
2. Velocity-dependent tension. Hill's equation shows the hyperbolic relationship between muscle velocity and muscle tension. Note that when an active muscle is pulled by an external load in the opposite direction of its intended contraction the muscle is "doing a negative" (as weightlifters say) and its velocity is less than zero. The tension per fiber is much greater in muscle fibers doing negatives than tension in a fiber going the same speed in the opposite (positive) direction.
3. Muscle fatigue. The FG (fast glycolytic) muscle fibers (white meat) that can exert the greatest maximum tension are the most easily fatigued. In Tandem04.m we model the fatigue as a first-order time constant that increases in duration as the maximum tension per fiber decreases.

Requirements:
(1) On each of the computers in the lab, in the Work folder of Matlab, is a folder Tandem that has a read-only file Tandem04.m function and its subroutines TanFly04, FatigueCalc.m and recruit_fiber.m. The call is
Tandem04(Wcnt, frce_thet, del_frce0, vmax, drg, fatigue_fac, k)
where the input arguments are
Wcnt the number of weak muscle fibers;
frce_thet the threshold force (torque) the strong biker must meet in the recruitment function;
del_frce0 the approx difference between strong and weak muscle torque used by the ODE solver;
vmax the zero-force velocity derived from Hill's equation:
drg the drag term from the model for the bicycle load;
fatigue_fac: increases time constant of fatigue onset: if less than 1.00 (but greater than 0) it means the rate of fatigue is increased;
k the term noted above, from Hill's formula for normalizing velocity or tension.

Tandem04.m is linked to colored notations for its various sections.

If you open Matlab and type at the command window
>> Tandem04(94, 2400, 90, 900, 14, 1.00, 0.2)
you will be asking for 94 weak fibers, with a pedal tension of 2400 units, a strong-weak force difference of 90 units, a vmax of 900 velocity units, a mechanical drag or friction of 14 units, a fatigue factor of 1.00 and constant k = 0.2 for Hill's equation normalization. When you run Tandem04.m with those conditions you will see that the strong muscle fatigues in 35 seconds, and a final fiber number vs tension plot looks like:

Your challenge: by adjusting the simulation parameters available to you (except for pedal tension), arrange that the "strong" biker fatigues at (say) 45 seconds.

(2) Pedal vs Resist on the tandem bike.
Inspect the stationary tandem bike. Note that the gear ratios for the two sets of chains connecting pedals to the rear flywheel are the same. Notice the mechanisms for tightening the chains. The two lab partners will sit on the bike seats facing each other, the longer-legged partner on the seat near the loose handlebars. You need to balance without holding onto anything with your hands. Place your hands palms down on the tops of your quads.

Who is stronger? Put your feet on the pedals and rotate until the pedals are in mirror image positions, where the top pedal for each rider is in a position to be pressed down with force. The "coxswain" will say "push!" and watch to see which way the chain moves, with both bikers temporarily exerting to the max. Whoever moves the chain in the positive direction will be "stronger". If the chain doesn't move at all it is arbitrary who will be "strong".

Next, the coxswain will look at his watch and say "start". The weak biker will let the strong biker pedal forward, while resisting, in cadence with the call of the coxswain, who will look for approx 0.5 Hz rotation of the pedals. The strong biker will be doing torque X radians of rotation amount of work, while the weak biker will be "absorbing" or resisting with the same amount of energy use. The coxswain can call out 15 second intervals. After a predetermined amount of time (between 1 and 5 minutes) the coxswain will say "Weak biker exert!" At that moment the weak biker will pedal has hard as he/she can, and we will see if the pedal rotation reverses, and to what speed in rad/sec.

After an interval of rest, try again, with a different duration of pedaling.

Notes:
The Machine shop modified a 50 year-old Schwinn tandem bicycle formerly owned by Profs Blume and Bower. The seat heights are a little difficult to adjust, and the chains sometimes slips off if pedaling is too fast (> 90 RPM).

The day after "the contest" the subject who resisted with negatives may feel sore leg muscles: Only by doing negatives can you increase muscle mass, as weightlifters know.

(3) We have not yet outfitted the tandem bike with instrumentation. Help design on paper instrumentation for the Tandem bike and riders. Answer the following questions as best you can. Place your answers in a Word file in your IP folder. The Word file may contain links to websites where a particular type of instrumentation is discussed.
a. What sensor can report (in volts) the rotation speed (RPM) of the bike pedals? Yes, you could monitor the rotation with a strobe light, but that would not report directly a voltage.
b. What can sense the tension in the arms of the pedals during rotation? And how could its response be relayed from the bicycle to a meter for display?
c. How can the oxygen use of a subject on the tandem bike be sensed and reported? Oxygen use would be a product of oxygen concentration (Inhale - Exhale) and the "tidal volume" per breath. So say how to measure the volume of a breath, and how to detect the concentration of oxygen in the exhaled air.
d. Say we want to monitor the temperature of the skin over the quadriceps muscle while the bike is being pedaled. What sort of sensor could do that to a 0.05 deg C accuracy? Provide a website link to your answer.
e. How could nerve/muscle activity of the quad be monitored? (EMG: ref a 123 Lab) What type and size and placement of electrodes do you recommend?

Possible FTQ: Will the time for fatigue of the strong biker in the simulation increase, decrease or stay the same, given a change to a parameter selected by JD or TA?

More challenging FTQ: What (nonlinear first-order) differential equation can account for the hyperbolic form of the velocity-force curve? See reading below.

Reading: pages 11-16, 30-35, from T. A. McMahon, Muscles, Reflexes and Locomotion.