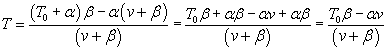Hill's equation for muscle tension vs <velocity of contraction>

Quick release experiments: Years before the protein constituents of muscle were known, experiments were done on the mechanical properties of isolated whole muscle. On page 10 of Muscles Reflexes and Locomotion (TA McMahon), dynamic ("quick-release") experiments on isolated muscle are described. A muscle is stretched to a constant length while stimulated to tetanus, then it is released against a variable load.
www.shadmehrlab.org
Below are shown a series of quick release length changes as suggested by the single graph of TAM's fig. 1.8(b).
Notice that there is a lever arm that rotates and that torque is involved in computing the effective load. The catch mechanism is a solenoid. Such experiments were started by A.V. Hill in the 1920s and continued by him after the interruption of WWII.

How to explain the sudden length change Δ x1? It is the result of a series elastic element (the tendon) that responds "instantly" to a change in force. There is no "t" in F = k*x.

The slower change to shortening Δ x2 is result of the muscle engaging and having a "dashpot-like" element, with a rate-of-change of shortening factor that creates a time constant (like a parallel RC circuit). See model from TAM Fig 6.7.

Digression to point out the gamma fiber feedback of muscle tension by Golgi tendon organ and the Ia fiber length change detector wrapped around the muscle spindle, or intrafusal muscle fiber. Propreoception! This activity of muscle tension and length provides a "seventh sense" which you however are not normally aware of. Conscious awareness of joint angle position come from free nerve endings in joint capsules.

Ia fibers are the basis of the stretch reflex through the spinal cord...which must be eliminated (example: Lab LT) to study muscle in isolation. Consideration of the stretch reflex will take us to the next topic of EN123, Automatic Control.

The v. weak intrafusal muscle spindles can be contracted by motoneurons, allowing the Ia fiber to extend its range of action and the extrafusal fibers are shorted and lengthed by external loads and motoneuron stimulation.

The length Δ x2 below decreases more in the top graph because the muscle has the opportunity to contract against the light load. As TAM requests, pay particular attention to the (negative) slope of the length change at time of release; that's the velocity of shortening, v. A tricky slope to measure accurately!

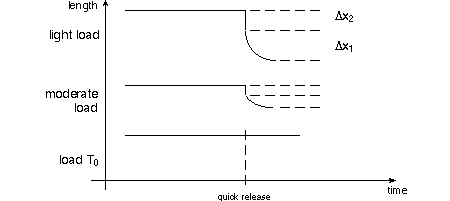
A series of quick release experiments will show an inverse relationship between load and velocity of shortening. Try to lift a 50lb suitcase as fast as you can and see how slow your muscles are! A. V. Hill fitted the data empirically to the equation

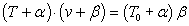
where v is shortening velocity (rate of contraction), T is the variable load and T0 is the particular load at which the the muscle doesn't change length. α and β are empirical constants. Since the term on the right contains neither v nor T, a curve of v vs T has a hyperbolic shape. (What are the asymptotes of the hyperbola? -α, -β)

It turns out that a wide variety of muscles tested by quick release result in about the same values of a and b, and that is the mechanical importance of Hill's equation.

When velocity v is zero then T = T0. (Considering how stimulated by nerve excitation the muscle is...) .

Maximum velocity of shortening occurs when T=0. (Except when the muscle could be pulled by an external force...)

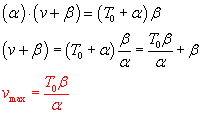
TAM says on p. 24, "For purposes of comparing different muscles, Hill's equation can be written in a normalized form,"

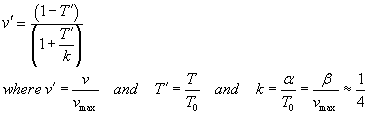
If T0 = Vmax = 1 then a = b = 0.25.

Both v' and T' will be between 0 and 1...

Can you see a way to get from Hill's equation to the normalized form? derivation
Can you show that ?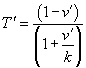

This equation for v' results in the plot on TAM page 15. A MATLAB script for such a plot is

tprime = [-.1 : .01 : 1.7];
k = 0.25;
vprime = (1 - tprime)./(1+tprime/k);
plot(vprime, tprime)
hold on, plot(tprime(11), vprime(11), 'r.')
grid on

Notice the period before the divide symbol; it's needed because tprime is a vector.
The semicolons after each line suppress printout. In plot the first variable is the "x-axis." On the normalized plot the tension is 1 at v = 0. In the plot, a red dot marks v=0.

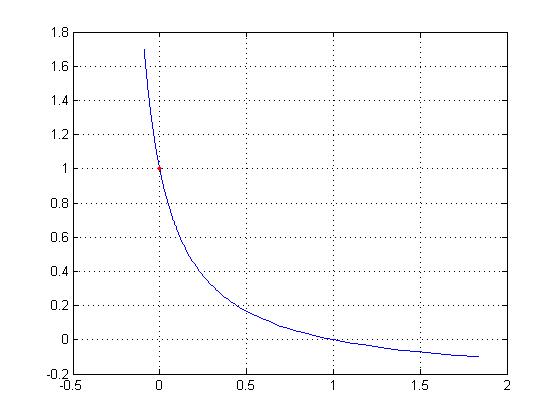
Negative velocity of muscle
Look at the plot of T vs v for Hill's equation, if v becomes negative. The force continues to increase: individual muscle fibers are "stronger". What does negative velocity mean? It means the muscle is being stretched during stimulation, instead of being able to contract.

Building muscle. Such stretching during stimulation pulls apart actin-myosin bridges and causes "micro-injury". The biochemical result of such injury is a signal for the muscle to strengthen by increasing in size. Muscle builders, like Arnold Schwarzenegger, are aware that "doing negatives" is the only way to build up muscle mass. A body builder lying on his back, on a bench, and pushing a weight up is bench pressing. While increasing the amount of weight bench pressed is a goal, a weight lifter almost never lifts weights in training. A spotter puts the weight in a cradle above the body builder, then the body builder slowly lowers the weight to his chest, doing a negative. Likewise, as you lower yourself during a pushup, you're doing a negative. The next day the muscle forced to negative velocities will be sore, a side effect of the micro-injuries and the process of developing more muscle.

We'll explore negative muscle velocity and muscle strength with the Tandem Bike experiment Lab VT.

Power. Power is energy/sec. Energy is force X distance. Therefore power is force X velocity. If a muscle is not moving it is generating no power. If the muscle is contracting as fast as it can against no load (no force) it is generating no power. Somewhere in-between 0 and maximum velocity is maximum power output for the muscle. In Hill's equation the term T·v has units of power.

Here's one way to isolate the power T·v in terms of v: Divide both sides of Hill's equation by v+B:

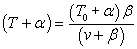
Subtract α from both sides and find a common denominator on the right:

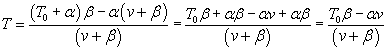
Since T·v = Power, we express power in terms of velocity:

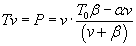
If we let a = b = .25, and T0 = 1, then power calculated and plotted in matlab, by
vv = [0:0.01:1];
pp = (vv.*(1*.25-.25*vv))./(vv+.25);
plot(vv, pp); grid on


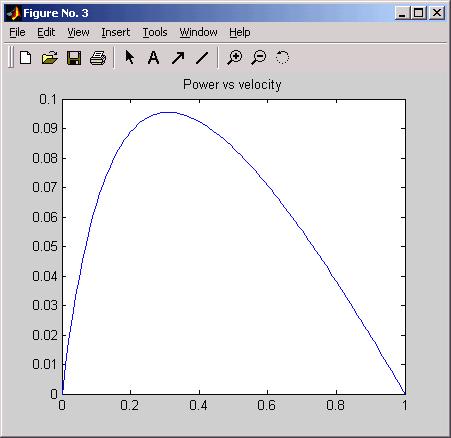
where it seems that maximum power occurs at about one third top speed.

From TAM:

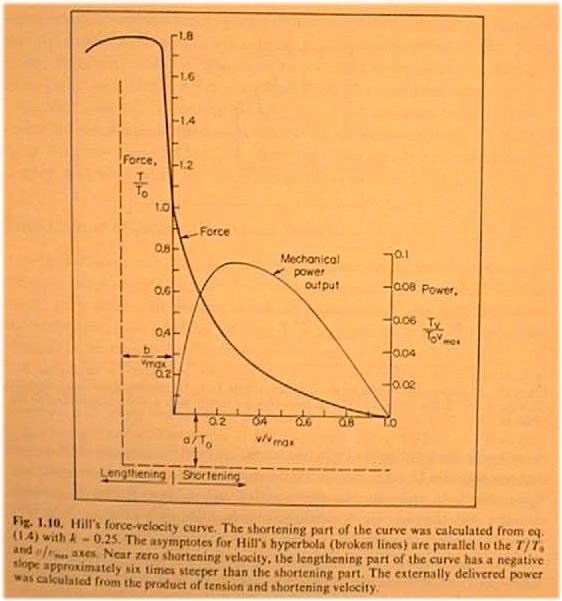
where optimal tension for maximum power is about 3/4 max tension.

If you allow velocity to be negative, with
vv = [-0.1:0.01:1];
you can see that the power of the muscles fibers can be much greater than in the positive direction.

Bicycling and power: When riding a bicycle with several gears you can feel the power-velocity relationship as you go up hill, gearing down until you're pedaling at an optimal rotation in cycles per minute to obtain maximum speed. Gear down too much and your pedals spin too fast to deliver much power to the bike chain.

Tandem bike demo: TAM says, "At a soiree of the Royal Society conducted by Hill in 1952 two subjects mounted a specially built tandem stationary bicycle. While one subject pedaled forwards the other resisted him through directly coupled pedals. At a speed of 35 RPM the subject pedaling forwards used 3.7 times as much oxygen per minute as the one pedaling backwards. It was demonstrated that a small woman, pedaling backwards, could rapidly exhaust a large man pedaling forward against her resistance. Since oxygen consumption and heat production are closely tied ... the muscles of the woman were presumably generating far less heat, even though the coupling of the pedals guaranteed that the forces and displacements experienced by the woman's feet were the same as those for the man's." (Same amount of work done: force X distance, but woman's muscles were "stronger", more efficient...)
See Lab VT write-up for more information.

Heat Generated by muscle: In chapter 2 of his book TAM shows how Hill later was able to derive his equation from thermodynamic considerations (measuring heat generated by muscle, finding that muscle is about 25% efficient converting chemical to mechanical energy). Contracting muscle, where crossbridges are being attached and detached frequently, generates the most heat. The energy-producing reaction of high-energy ATP to ADP + phosphate produces the heat.

From TAM chpt 2: "Most of what is known about heat production in muscle derives from the work of A. V. Hill and his collaborators, beginning in 1910 immediately after Hill finished his undergraduate course, and continuing for sixty years." and more...

A single twitch increases the temperature of a muscle by about 3x10^-3 deg C...

To begin with, all Hill knew were the changes in heat, not the underlying chemical reactions...

Hill's glossary:
Resting heat
Initial and recovery heat
Activation heat
Shortening heat: The Fenn effect

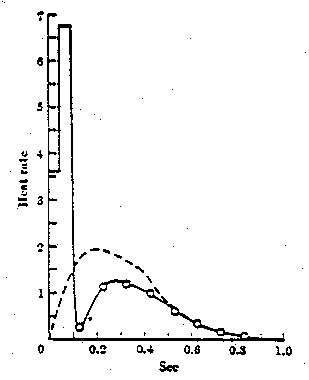
http://www.uic.edu/classes/phyb/phyb516/energeticsu3.htm

TAM p. 34: equation from thermodynamics rearranged into the mechanical Hill equation. "Hill plotted the rate at which total energy is liberated in shortening (T+a)*v where v = -xdot...against muscle tension T..."

Muscle fatigue: We've already noted that fast twitch muscles are easily fatigued because they use anaerobic metabolism to restore ATP.

We can also tell you that the six eye muscles of each eye are so over-engineered (over-evolved?) that they cannot be fatigued except by starvation. As a consequence, the signals from motoneurons to control eye position are an accurate measure of where the eyes are looking (in the dark, for example) and we humans have no apparent need for proprioception in the eye muscles (although tendon organs and muscle spindles are present).

R.H. Fitts, "Cellular Mechanisms of Muscle Fatigue," Physiological Reviews 14: 49-92 (Jan 1994).

"The major source of acid production in skeletal muscle is the anaerobic production of lactic acid from glucose and glycogen..."

"It is now well known that fast motoneurons and fast motor units fatigue more rapidly and to a greater extent than slow muscles and slow motor units..."

Fatigue of sprinters vs marathon runners...
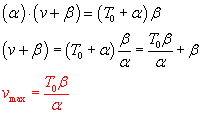
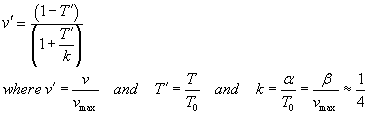
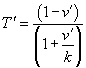