Nernst Potential and Nerve Conduction Speed (2007-08)

Topics:
¶ concentration gradients and Nernst potential
¶ Cable theory, length constant and nerve conduction

Remember thermocouples, where two metals, dissimilar in mobility, are welded together and their interface is able to generate a microvolt-size potential difference.

In the biology case here, a membrane separates two ionic solutions (electrolytes). What potential develops across the membrane and what chemical reactions occur at metal-aqueous interfaces is our subject here. We also consider at what speed a pulse signal (action potential) can propagate down an axon "cable".

Anions(+) and cations(-) in the electrolyte carry the electrical current normally handled by electrons in metal wires.

Distribution of some ions in mammalian tissue
Some data from Gary G. Matthews, Cellular Physiology of Nerve and Muscle, Blackwell Scientific Publications, Boston (1991).

A- represents negatively charged proteins.

Inside a cell considerable calcium is sequestered. For example, from the endoplasmic reticulum of muscle cells Ca++ is released when the cell is stimulated.

Cells have ionic pumps that maintain concentration gradients. The ions themselves can "diffuse" in or out of the cell through specialized protein channels.

Reading:
George B. Benedek & Felix M. H. Villars, Physics With Illustrative Examples from Medicine and Biology, Vol 3: Electricity and Magnetism, Addison-Wesley, Reading, Massachusetts (1979).

Howard C. Berg, Random Walks in Biology, Princeton Univ. Press (1983). A statistical physics look at the diffusion-drift development that leads to the Nernst potential (p. 141). Berg is well-known for his "Life at low Reynolds number" essay: see p. 75 of the book.

Bertil Hille, Ion Channels of Excitable Membranes, Sinauer Associates, 814 pp., (2001)

Fick's First Law
Consider diffusion flux J along one dimension: where the last form is the gradient in 3D.
In these equations J is a flux [a vector, particles/(area-sec)] and concentration is C at point x. D is the diffusion coefficient, and has dimensions of cm^2/sec. Notice the minus sign! A positive concentration gradient leads to a negative direction for diffusion. See figure below. Imagine we're considering a concentration gradient for K+=potassium ions across a cell's membrane.

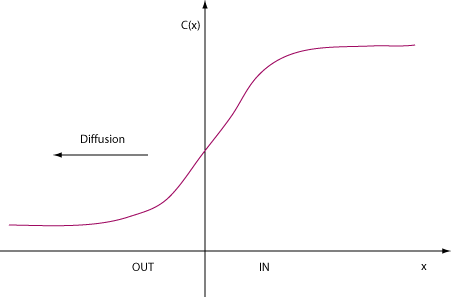
Flux as current: Fick's 1st Law tells us about a diffusive flux of particles, charged or uncharged. For example, glucose is an uncharged particle in solution, and is subject to Fick's Law just as well as charged K+ and Cl-, but glucose flux is NOT a current! A flux of anions (+) is a positive current in the same direction as the flux, while a flux of chloride cations (-) is a current in the opposite direction.

The diffusion of charged particles (in the case we're considering, of K+) will set up an E field which will oppose the diffusion flux, and in fact will set up a voltage difference across the membrane.

Consider also that charged ions going in and out of a cell are going in and out of a fairly confined space, and the charge accumulation or deficit can be enough to generate a significant E field across the membrane. Even outside the cell space is rather confined, with the spacing between cells again able to be measured in angstroms, leaving "outside" not the same as a resevoir.

Drift of charged particles in an E field. In a material, charged particles will "drift" with a velocity proportional to their mobility μ, their charge, and the strength of the E field:

If the charged particles were in a plasma they would move under the influence of F=ma, accelerating, but here in a material the particle reach a "terminal velocity". (Demo with corn syrup, where a ball bearing falls faster under the influence of gravity than a marble of the same size.)
mobility μ is a property of a particle in a material (in this case aqueous electrolyte, and has units cm/(sec N ) .

The flux due to drift in the E field will be proportional to the concentration of the ions.
(which can be morphed to Ohm's Law, and, again, compare to F = ma)

We can now combine the diffusion flux and the drift flux in a steady-state version of KCL (flux as current with explicit account taken of area normal to current flow).

We need to relate diffusion constant D to mobility μ : Einstein found
(in metals), where gas constant R and Boltzmann constant k are related by
R = kN, where N is the number of molecules in question. (ref: Van Vlack, Elements of Materials Science 2nd Ed. Addison-Wesley, 1964. pp 105, 98). As a result (considering other material factors too), when temperature rises, diffusion coefficient D always increases while mobility μ increases for non-metals and decreases for metals. Further information: in F. Reif, Statistical Physics McGraw-Hill, New York, (1967), page 337 shows that, in general, .

Rewriting the flux equation, we have

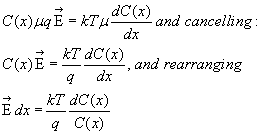
where you can see that temperature T is still involved but mobility μ has cancelled out. Later, when different ionic species have their own mobility, various μ's will survive in a multi-ion formula.

Definition of potential difference = voltage. Now we need to remind you that
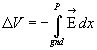Since this integral is "conservative" you can go along any path from gnd to point P (in our case, from outside to inside the cell, across the membrane). Therefore integrate the flux balance equation to end up computing voltage. We will be grounding the extracellular space, called OUT in the integral.

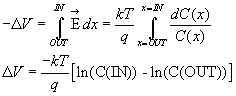
Remembering log(X) - log(Y) = log(X/Y), and computing that, at room temperature, kT/q = 25 mV we have
,the Nernst equation for a singly-charged positive ionic species at room temperature. Consider a ratio of internal to external potassium of 10:1, we find that VK = -58 mV, which turns out to be what is measured.

E field strength across the membrane: 70 mv divided by 10 Angstroms ~= 100M V/meter... near the breakdown strength...

What happens to the Nernst potential if calcium instead of potassium is considered? Ans: Calcium is Ca++, a doubly charged ion, in solution. Therefore substitute 2q in the kT/q term of the Nernst equation. The Nernst voltage is reduced by a factor of 2! Think of it this way: in the same E field a Ca++ ion will experience twice the force as a K+ ion. Therefore half the field strength would be needed to exert the same force on Ca++.

What happens if chloride ion is considered in a Nernst potential calculation? There are two ways to think about that question: (1) Since chloride ion has the opposite sign of K, then all other things being equal, the sign of the answer for the Nernst potential should be opposite to that of potassium. (2) Since chloride has a higher concentration outside than inside the cell, then the sign of the answer should be the same as potassium.

Where does the sign change come in when considering negatively charged ions? Consider the diffusion flux. If chloride Cl- concentration is greater OUT than IN the direction of diffusion of chloride ions from OUT to IN (left to right below). But because chloride has a negative charge, the direction of the chloride diffusion current will be opposite, from right to left.

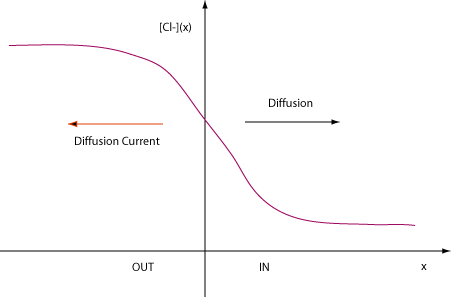
Therefore the diffusion current term in the flux balance will have the opposite sign for a negatively charged ion.

Now consider the drift flux due to the electric field of charge separation. In our K+ equation the term q was +e, where e is the magnitude of the charge on an electron. Now q becomes -e for the chloride ion. But the electric field changes direction too, because negative charges instead of positive charges have moved into position to block the further diffusion of chloride ions. You can write the drift equation as

and you see it will have the same sign as the potassium version. Thus the only effective sign change occurs in the diffusion flux term, and we will expect a sign change in the answer if we're considering Cl- to have the same concentration gradient as K+.

Given the concentration gradient of sodium Na+, what will be the sign of the "sodium equilibrium potential" (Nernst potential considering sodium alone)? Because sodium concentration is higher outside the cell than in, it's Nernst potential will be positive, and will follow the same Nernst equation logarithmic law as potassium.

Protein as pumps and channels for ions. We have been working with mobilities of ions as factors in their Nernst potentials. In fact, most ions move relatively freely inside and outside the cells; it's at the membrane barrier that mobility becomes important. We understand that ionic imbalances are maintained by pumps, in the form of proteins in the cell membrane, in somewhat the same way that an air conditioner in a window helps maintain a temperature gradient from inside to outside the house. Proteins also form channels for specific ions, and the permeability (a more common term for ionic mobility in the membrane) of a channel can be modulated by synaptic activity or transmembrane voltage. It is possible to record, by means of a patch clamp electrode isolating a small section of membrane, the signals of individual channels. See below, from www.ccs.fau.edu/~liebovitch/ dyn.html

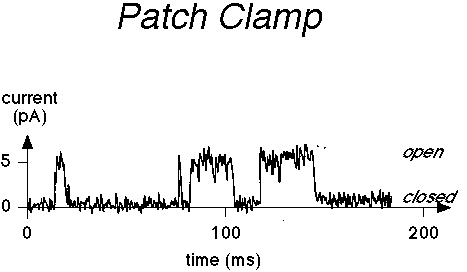
Reading Bertil Hille, Ion Channels in Excitable Membranes, 3rd Ed., Sinauer Associates (2001).

The 1991 Nobel Prize in Physiology or Medicine went to Bert Sakmann and Erwin Neher for their work on patch clamping.

EXAMPLE: Say the concentration of K+ and Cl- is the same C(x) everywhere and that the mobility of K+ > mobility Cl-. What is an expression for the transmembrane voltage? ANS: You need to add up the fluxes of K+ and Cl-. We already have the K+ flux:

and the Cl- flux sum will be
because the Cl- diffusion flux is in the opposite direction, but the electrical flux is the same direction. Add the two contributions up, sum to zero, separate variables and see

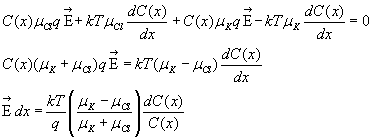
now integrate from OUT to IN, as before, and obtain
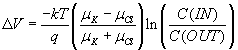, which gives the potassium-only answer from before if μCl = 0.

Another problem: Now assume the concentrations differences of sodium and potassium are equal and opposite across a membrane. If the mobilities of Na and K are equal, then the transmembrane voltage will be zero. In fact the voltage is negative, in the direction of the K equilibrium potential. Assume the mobility of K > mobility of Na ions. What will be the voltage difference? Note that if C(x) is the potassium concentration function, then the Na concentration function is C(-x). Furthermore ... How far can you get?
A better approach, when the concentration gradients of the ionic species differ: compute independently the Nernst potential of each ionic species. Then use superposition and compute the total of the respective ionic mobilities, for a weighted sum:

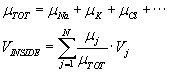
where N is the total number of ionic species, and Vj is the Nernst potential of the jth species.
Example. Assume the concentration gradients of Na and K are equal and opposite, +58 and -58mV. Suppose at rest the mobility of K is 3 times greater than the mobility of Na. Then Vinside = 0.75*(-58) + 0.25*58 = -29mV.

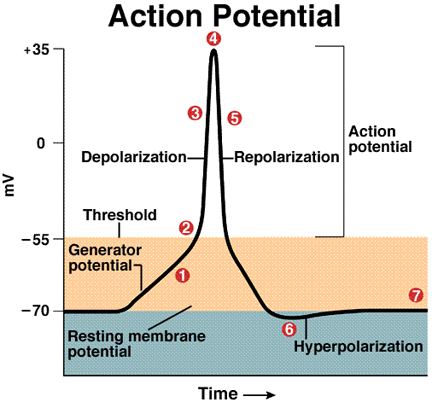
Increase in Na+ permeability during excitation: In the resting state of a nerve cell sodium mobility across the membrane is much lower than potassium, and the cell maintains a negative voltage. When a nerve or muscle cell is stimulated by synaptic transmission, the mobility (or channel conductance, or permeability) for sodium transiently increases to a value greater than that for potassium and the cell internal voltage "spikes" above zero volts for about a millisecond. (image below from http://www.bio.psu.edu/Courses/Fall2002/Biol142/neurons/neurons.html)

------------------------------------------------------------------------------
Cable Theory for nerve axon length and time constants, and conduction velocity:

The following assumes passive conduction of voltage changes down an axon or dendrite. Consider a cylindrical tube as a model for a dendrite or axon process. The wall of the tube will be a high resistance membrane and the inside of the tube will be low resistance axoplasm.

Say the inside of the tube has resistance/length = r-in, as shown below.


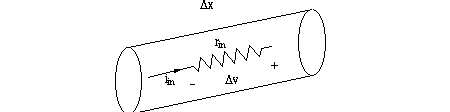
How will r-in depend on cable diameter? Consider the material property we called rho in strain gauge development: here it will appear again, as specific axial resistance of "axoplasm", and its value is about 100 Ω--cm. Therefore r-in = rho/area.

Conductance g-in = 1/r-in will increase as the square of the diameter.

Now consider the leakage current im going out of the membrane. Per "compartment" of length we have a picture like,

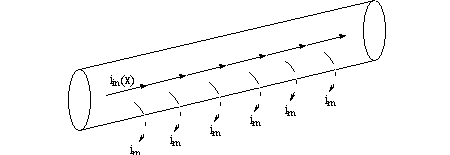
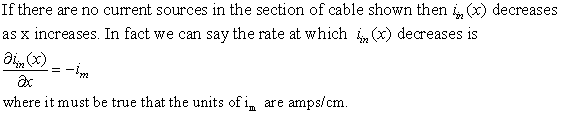
If you differentiate again and substitute the above equation in, you have

where the minus signs cancel out.

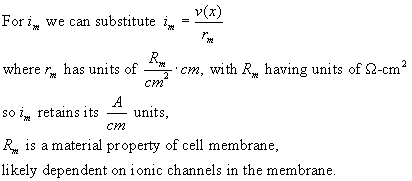
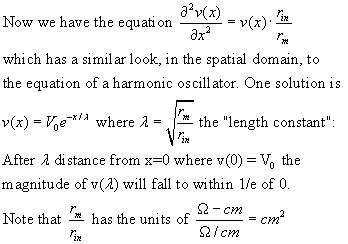
Now on to the time domain: Consider that there is capacitance in the membrane:

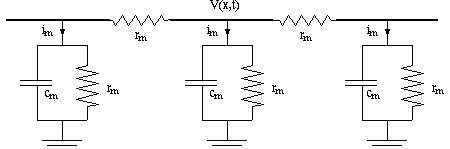
the membrane current is now to be expressed as:

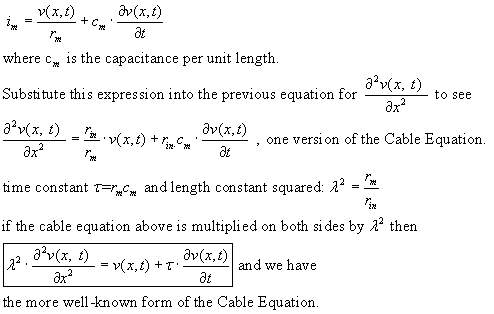
How are r-in, r-m and c-m calculated from physical properties of the cell and its membrane? Recall from the strain gauge lecture that resistance R, in ohms, for a rod of length L and cross-section A is

where rho is the resistivity of the material of the rod. The units of resistivity are Ohm-cm. Resistance per unit length, by a "dimensional analysis," is therefore

where d is the diameter of the cable under consideration. Therefore knowing radius r allows calculation of resistance r-in.

It is known that resistivity of axoplasm is 100 Ohm-meter (From Neuron to Brain , p. 141)
Compare this to the resistivity of metal, like copper: about 10^-8 ohm-m!
Axoplasm is the same order as crystal silicon resistivity.

What's the resistance of a 1 cm long axon, diameter 10 microns? about 10^10 Ohms!

Next, consider membrane as a sheet of material specified by capacitance/cm^2 Cm, and by conductance/cm2 Gm. Conductance has units of mhos. Why use conductance? It's proportional to the area of the membrane under consideration. For a cable of diameter d, the circumference is pi·d. So pi·d*1cm is the area of a unit length (cm) of membrane. Capacitance per unit length c-m is then Cm·pi·d and conductance per unit length is Gm·pi·d. therefore

Both capacitance per unit length and resistance per unit length can therefore be calculated from material properties of membrane.
Membrane has 1 muF /cm^2 and a RESISTANCE of about 2000 Ohms/cm^2
These factors allow calculation of time constant and length constant of membrane.
A passive voltage change will decay toward zero with length constant lambda.

Solutions to the cable equation: See D. J. Aidley, The Physiology of Excitable Cells, page 50 ff and
B. Katz, Nerve, Muscle and Synapse, Oxford Univ Press (1970)

Myelination significantly increases Rm and therefore increases the length constant of a axon, typically from 10 to 2000 microns! The nodes of Ranvier are closer than one length constant. A myelin wrap can also reduce membrane capacitance (remember capacitors in series?) so the effective time constant of the membrane is about the same; the result is faster propagation of an action potential in a myelinated axon.

Calculating the speed of conduction down a cable:

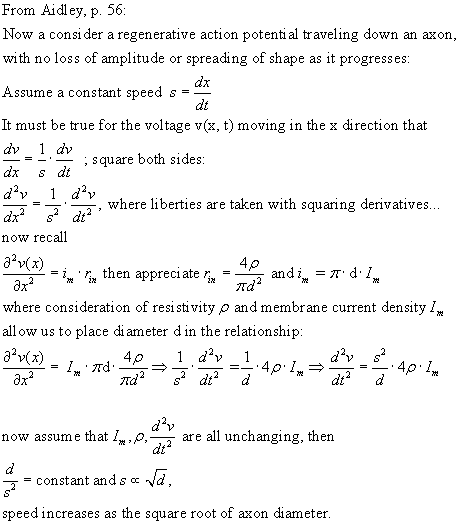
From ICHIJI TASAKI, "ON THE CONDUCTION VELOCITY OF NONMYELINATED NERVE FIBERS," Journal of Integrative Neuroscience, Vol. 3, No. 2 (2004) 115–124.

The cable equation is a PDE; run matlab function pdex4.m to see a related example. For both time and position x, V can vary. a 3-D plot is needed.
C:\MatlabR12\Toolbox\Matlab\demos