Metal - Aqueous interface: How current flows through electrolytic fluids (11/03 update)

Topics:
¶ concentration gradients and Nernst potential
¶ metal-electrolyte reactions
¶ electrode circuits for neural stimulation

Remember thermocouples, where two metals, dissimilar in mobility, are welded together and their interface is able to generate a microvolt-size potential difference.

In the biology case here, a membrane separates two ionic solutions (electrolytes) What potentials develop at cell membranes and what chemical reactions occur at metal-aqueous interfaces is our subject here.

Anions(+) and cations(-) in the electrolyte can carry the electrical current normally handled by electrons in metal wires.

Distribution of some ions in mammalian tissue
Some data from Gary G. Matthews, Cellular Physiology of Nerve and Muscle, Blackwell Scientific Publications, Boston (1991).

A- represents negatively charged proteins.

Inside a cell considerable calcium is sequestered. For example, from the endoplasmic reticulum of muscle cells Ca++ is released when the cell is stimulated.

Cells have ionic pumps that maintain concentration gradients. The ions themselves can "diffuse" in or out of the cell through specialized protein channels.

Reading:
George B. Benedek & Felix M. H. Villars, Physics With Illustrative Examples from Medicine and Biology, Vol 3: Electricity and Magnetism, Addison-Wesley, Reading, Massachusetts (1979).

Howard C. Berg, Random Walks in Biology, Princeton Univ. Press (1983). A statistical physics look at the diffusion-drift development that leads to the Nernst potential. Berg is well-known for his "Life at low Reynolds number" essay: see p. 75 of the book.

Fick's First Law
Consider diffusion flux J along one dimension: where the last form is the gradient in 3D.
In these equations J is a flux [a vector, particles/(area-sec)] and concentration is C at point x. D is the diffusion coefficient, and has dimensions of cm^2/sec. Notice the minus sign! A positive concentration gradient leads to a negative direction for diffusion. See figure below. Imagine we're considering a concentration gradient for K=potassium ions across a cell's membrane.

Flux as current: Fick's 1st Law tells us about a diffusive flux of particles, charged or uncharged. For example, glucose is an uncharged particle in solution, and is subject to Fick's Law just as well as charged K+ and Cl-, but glucose flux is NOT a current! A flux of anions (+) is a positive current is the same direction as the flux, while a flux of chloride cations (-) is a current in the opposite direction.

The diffusion of charged particles (in the case we're considering, of K+) will set up an E field which will oppose the diffusion flux, and in fact will set up a voltage difference across the membrane.

Drift of charged particles in an E field. In a material, charged particles will "drift" with a velocity proportional to their mobility μ, their charge, and the strength of the E field:

If the charged particles were in a plasma they would move under the influence of F=ma, accelerating, but here in a material the particle reach a "terminal velocity". (Demo with corn syrup, where a ball bearing falls faster under the influence of gravity than a marble of the same size.)
mobility μ is a property of a particle in a material (in this case aqueous electrolyte, and has units cm/(sec N ) .

The flux due to drift in the E field will be proportional to the concentration of the ions.
(which can be morphed to Ohm's Law, and compare to F = ma)

We can now combine the diffusion and drift flux in a steady-state version of KCL (flux as current with explicit account taken of area normal to current flow).

We need to relate diffusion constant D to mobility μ : Einstein found
(in metals), where gas constant R and Boltzmann constant k are related by
R = kN, where N is the number of molecules in question. (ref: Van Vlack, Elements of Materials Science 2nd Ed. Addison-Wesley, 1964. pp 105, 98). As a result (considering other material factors too), when temperature rises, diffusion coefficient D always increases while mobility μ increases for non-metals and decreases for metals. Further information: in F. Reif, Statistical Physics McGraw-Hill, New York, (1967), page 337 shows that, in general, .

Rewriting the flux equation, we have

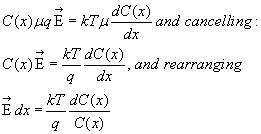
where you can see that temperature T is still involved but mobility μ has cancelled out. Later, when different ionic species have their own mobility, various μ's will survive in a multi-ion formula.

Definition of potential difference = voltage. Now we need to remind you that
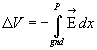Since this integral is "conservative" you can go along any path from gnd to point P (in our case, from outside to inside the cell, across the membrane). Therefore integrate the flux balance equation to end up computing voltage. We will be grounding the extracellular space, called OUT in the integral.

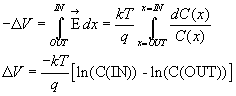
Remembering log(X) - log(Y) = log(X/Y), and computing that, at room temperature, kT/q = 25 mV we have
,the Nernst equation for a singly-charged positive ionic species at room temperature. Consider a ratio of internal to external potassium of 10:1, we find that VK = -58 mV, which turns out to be what is measured.

What happens to the Nernst potential if calcium instead of potassium is considered? Ans: Calcium is Ca++, a doubly charged ion, in solution. Therefore substitute 2q in the kT/q term of the Nernst equation. The Nernst voltage is reduced by a factor of 2! Think of it this way: in the same E field a Ca++ ion will experience twice the force as a K+ ion. Therefore half the field strength would be needed to exert the same force on Ca++.

What happens if chloride ion is considered in a Nernst potential calculation? There are two ways to think about that question: (1) Since chloride ion has the opposite sign of K, then all other things being equal, the sign of the answer for the Nernst potential should be opposite to that of potassium. (2) Since chloride has a higher concentration outside than inside the cell, then the sign of the answer should be the same as potassium.

Where does the sign change come in when considering negatively charged ions? Consider the diffusion flux. If chloride Cl- concentration is greater OUT than IN the direction of diffusion of chloride ions from OUT to IN (left to right below). But because chloride has a negative charge, the direction of the chloride diffusion current will be opposite, from right to left.

Therefore the diffusion current term in the flux balance will have the opposite sign for a negatively charged ion.

Now consider the drift flux due to the electric field of charge separation. In our K+ equation the term q was +e, where e is the magnitude of the charge on an electron. Now q becomes -e for the chloride ion. But the electric field changes direction too, because negative charges instead of positive charges have moved into position to block the further diffusion of chloride ions. You can write the drift equation as

and you see it will have the same sign as the potassium version. Thus the only effective sign change occurs in the diffusion flux term, and we will expect a sign change in the answer if we're considering Cl- to have the same concentration gradient as K+.

Given the concentration gradient of sodium Na+, what will be the sign of the "sodium equilibrium potential" (Nernst potential considering sodium alone)? Because sodium concentration is higher outside the cell than in, it's Nernst potential will be positive, and will follow the same Nernst equation logarithmic law as potassium.

Protein as pumps and channels for ions. We have been working with mobilities of ions as factors in their Nernst potentials. In fact, most ions move relatively freely inside and outside the cells; it's at the membrane barrier that mobility becomes important. We understand that ionic imbalances are maintained by pumps, in the form of proteins in the cell membrane, in somewhat the same way that an air conditioner in a window helps maintain a temperature gradient from inside to outside the house. Proteins also form channels for specific ions, and the permeability (a more common term for ionic mobility in the membrane) of a channel can be modulated by synaptic activity or transmembrane voltage. It is possible to record, by means of a patch clamp electrode isolating a small section of membrane, the signals of individual channels. See below, from www.ccs.fau.edu/~liebovitch/ dyn.html

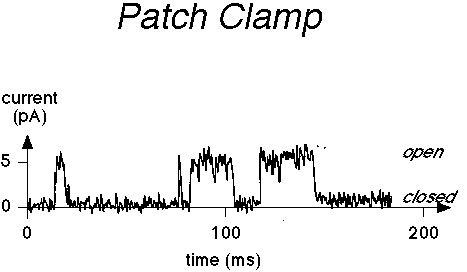
Reading Bertil Hille, Ion Channels in Excitable Membranes, 3rd Ed., Sinauer Associates (2001).

The 1991 Nobel Prize in Physiology or Medicine went to Bert Sakmann and Erwin Neher for their work on patch clamping.

EXAMPLE: Say the concentration of K+ and Cl- is the same C(x) everywhere and that the mobility of K+ > mobility Cl-. What is an expression for the transmembrane voltage? ANS: You need to add up the fluxes of K+ and Cl-. We already have the K+ flux:

and the Cl- flux sum will be
because the Cl- diffusion flux is in the opposite direction, but the electrical flux is the same direction. Add the two contributions up, sum to zero, separate variables and see

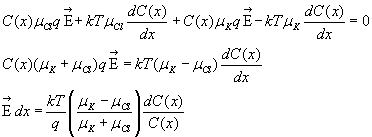
now integrate from OUT to IN, as before, and obtain
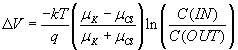, which gives the potassium-only answer from before if μCl = 0.

Another problem: Now assume the concentrations differences of sodium and potassium are equal and opposite across a membrane. If the mobilities of Na and K are equal, then the transmembrane voltage will be zero. In fact the voltage is negative, in the direction of the K equilibrium potential. Assume the mobility of K > mobility of Na ions. What will be the voltage difference? Note that if C(x) is the potassium concentration function, then the Na concentration function is C(-x). Furthermore ... How far can you get?
A better approach, when the concentration gradients of the ionic species differ: compute independently the Nernst potential of each ionic species. Then use superposition and compute the total of the respective ionic mobilities, for a weighted sum:

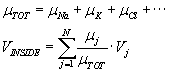
where N is the total number of ionic species, and Vj is the Nernst potential of the jth species.
Example. Assume the concentration gradients of Na and K are equal and opposite, +58 and -58mV. Suppose at rest the mobility of K is 3 times greater than the mobility of Na. Then Vinside = 0.75*(-58) + 0.25*58 = -29mV.

Increase in Na+ permeability during excitation: In the resting state of a nerve cell sodium mobility across the membrane is much lower than potassium, and the cell maintains a negative voltage. When a nerve or muscle cell is stimulated by synaptic transmission, the mobility (or channel conductance, or permeability) for sodium transiently increases to a value greater than that for potassium and the cell internal voltage "spikes" above zero volts for about a millisecond. (image below from http://www.bio.psu.edu/Courses/Fall2002/Biol142/neurons/neurons.html)

------------------------------------------------------------------------------
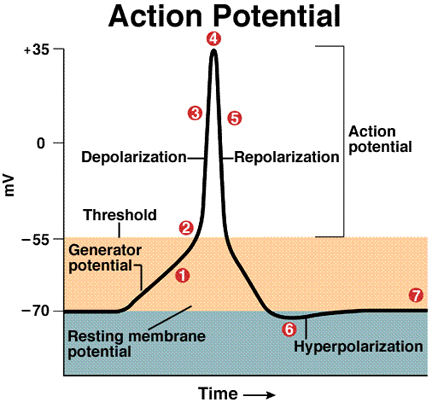
Chemical reactions at the metal-aqueous interface
¶electrodes as another kind of "sensor"
¶the nature of skin as a aqueous interface.

Reading: see Derenzo, page 177, and Daniel Harris, Quantitative Chemical Analysis, W.H. Freeman (1987) chpt 15.

DEMO: a lemon or potato "battery" with various pairs of metal electrodes: (Fe, Al, Au, Cu, Z, Ag, W...) Zinc, and silver for example, inserted through the rind results in a voltage of about 1.1v. Imagine the 1.1v in series with an output resistance.

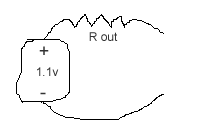
Place a 20K ohm load between the electrodes on the battery and watch voltage drop, to reveal the size of the output resistance. What do you calculate the output resistance to be? How much power can the battery deliver?!

You can work out what to expect from various metal combinations in aqueous solutions with a Table of Standard Reduction Potentials

Metal electrodes in water. Imagine one terminal of a 9v. battery connected to a silver wire in cup of water, and the other terminal to another Ag wire in the same cup. At the negative terminal two electrons will combine with 2 H+ ions which will combine to form H2. At the positive terminal an Ag atom will oxidize, giving up an electron e- and going into solution as Ag+, basically replacing the lost H+ at the negative electrode. Will the Ag+ combine with OH- to form AgOH?

The "resistance" of the water between the electrodes will be relatively high because the concentration of ions in distilled water is only 10^-7.

Electrode in saline: What will happen if NaCl is dissolved in the water (creating saline), with 2 battery terminals in place? see below, where we have added an agar bridge between the electrodes.

Terminology: If an electrode delivers electrons to a solution it is acting as a cathode, and oxidation occurs at the electrode. If it accepts electrons (or negative ions), it is an anode.

Let's follow an electron down the wire to the cathode. Imagine the electron comes from a reaction at the tip of the silver wire, Ag > Ag+ + e-. The electron combines with a sodium ion, removing a positive charge from the solution and creating (briefly) elemental sodium. The elemental sodium reacts quickly with water to produce sodium hydroxide and hydrogen gas. You see gas bubbling at the cathode. The sodium hydroxide ionizes completely.
Na+ + e- --> Na
2 Na + 2 H2O --> 2 NaOH + H2 (gas)
NaOH --> Na+ + OH-
The overall reaction, powered by the battery, can be described as:
2 Ag + 2 Na+ + 2 H2O --> 2Ag+ +2 H2 + 2 Na+ +2 OH-
where there are now two silver ions in solution and 2 more hydroxy negative ions created, in solution, and H2 gas bubbles; the hydroxy ions represent the continuation of the free electron current from the wire in the solution. (B&V vol 3, p. 79)

At the Ag-saline anode electrode the a Cl- ion reacts with Ag to release an electron: Ag + Cl- --> AgCl + e- . Silver chloride is a stable salt, and will form a grey coating on the shiny silver wire.

Notice the difference in electrode reactions between distilled water and saline. In particular, if you try the experiment with a 9v battery and iron nails for electrodes, you will see a healthy wellspring of bubbles in the case of saline, but no bubbles in the case of distilled water. Because of the 5 orders of magnitude difference between ion concentration in H2O and saline, the production of H2 in water is 5 orders of magnitude less. The lack of electrical conductivity of water leads to its application as a cleaning agent for electrical equipment, in particular, cleaning insulators near high voltage power lines, with the water under pressure coming out of fire hoses.

Electroplating: If the solution were silver chloride and the electrode was, say, tin, then Ag+ would react with the free electron at the cathode, and would form elemental silver that would plate onto the electrode. The electrode would become silver plated tin. Thus the cathodic reaction can in some cases be described as a plating electrode, an important process in the jewelry industry of Providence.

What happens to the tin (Sn) atom that gave up the electron? It goes into solution and is replaced by the silver atom. See below for another example:

Reading: Philip H. Rieger, late of the Chem Dept at Brown, wrote Electrochemistry, 2nd Edition, Chapman-Hall (1993), DD553.R3. On p. 398 he says, "...to plate copper on a steel substrate the object to be plated is made the cathode in an electrolysis cell where a piece of copper is used as the anode. There are many subtleties, however, which must be considered in practice. Thus, in plating copper on steel, for example, we immediately recognize that the reaction
Cu2+ (aq) + Fe(s) --> Cu(s) + Fe2+(aq)
is spontaneous. To prevent the dissolution of iron from the substrate, the activity of Cu2+(aq) must be reduced by the addition of a complexing agent which coordinates strongly to Cu(II) but much less so than Fe(II)... In electroplating applications, it is usually desirable to deposit a layer of uniform thickness. This requirement is not difficult to meet if the substrate has a simple geometry. If there are holes or recesses, however, a uniform layer can be quite difficult to achieve."

Rieger goes on to analyze methods for improving the plating of holes, noting that the addition of inert electrolyte can lower the IR drop for the current path trying to reach the holes, and addition of a wetting agent to facilitate the release of H2 bubbles from the holes.

Etching: If the electrolyte were NaOH (sodium hyroxide), and the anode a thin tungsten (W) wire, and the other electrode a "carbon reference" (like the center pole in a D battery) then the anode reaction would etch W atoms off into the solution.

Demo: The output of a variac connected to tungsten and reference electrodes, and set at about 10v RMS, can etch the tungsten wire (125 μ diam) to a sharp smooth point, so fine it can't be resolved under a light microscope (< 1 μ ). Both phases of the AC cycle can etch:
W > W+ e- > and e- + Na+ > Na (Na combines with H20 then, and generates H2 gas...)
W + Cl- > WCl + e-
such etched electrodes, dipped in epoxy to limit exposed metal to a 20 micron length, are useful for single unit recording from CNS neurons. At 500 Hz such electrodes will have about 500K ohms of impedance.

Other versions of such etching reactions can be thought of as corrosion, and are responsible for the degradation of buried metal pipes in wet soil.

AgCl electrodes: Electrochemical reactions with pure silver are electrically noisier than the Ag-AgCl reaction. The AgCl coating is a good buffer. The elemental silver at the surface changes to a AgCl film, which may ionize partially to Ag+ and Cl- in solution. With AgCl coating on the cathode the reaction changes to: (B&V vol 3, p 79)
e- + AgCl > Ag + Cl-
thus elemental Ag is removed from one electrode and silver chloride powder ends up coating the other electrode.

2006. Instrumentation for ion monitoring: Potentiostat: A potentiostat can keep track of ion concentration by balancing the voltage between "working" and reference electrodes while passing current through a control electrode. For example, the amount of gold in solution for electroplating can be monitored by a potentiostat. (Technics, Cranston RI). see website from Hebrew University Chemistry Dept for more information.

Reading: Geddes' Book (R856/G43/1975) pages 198-215
Practical tips for electrodes attached to humans:
Webster book. page 280:
avoid solder (lead Pb), and dissimilar metal contacts
Use good surgical tape and conductive cream
avoid flexing wires at contact, and make sure there is strain relief.
beware of moisture under insulation
Use AC coupling and an isolation amplifier for patient safety

Can abraid the skin with sandpaper to remove a layer of epidermis and lower impedance.
Smaller electrode size means better spatial localization. Ground electrode can be a large plate.